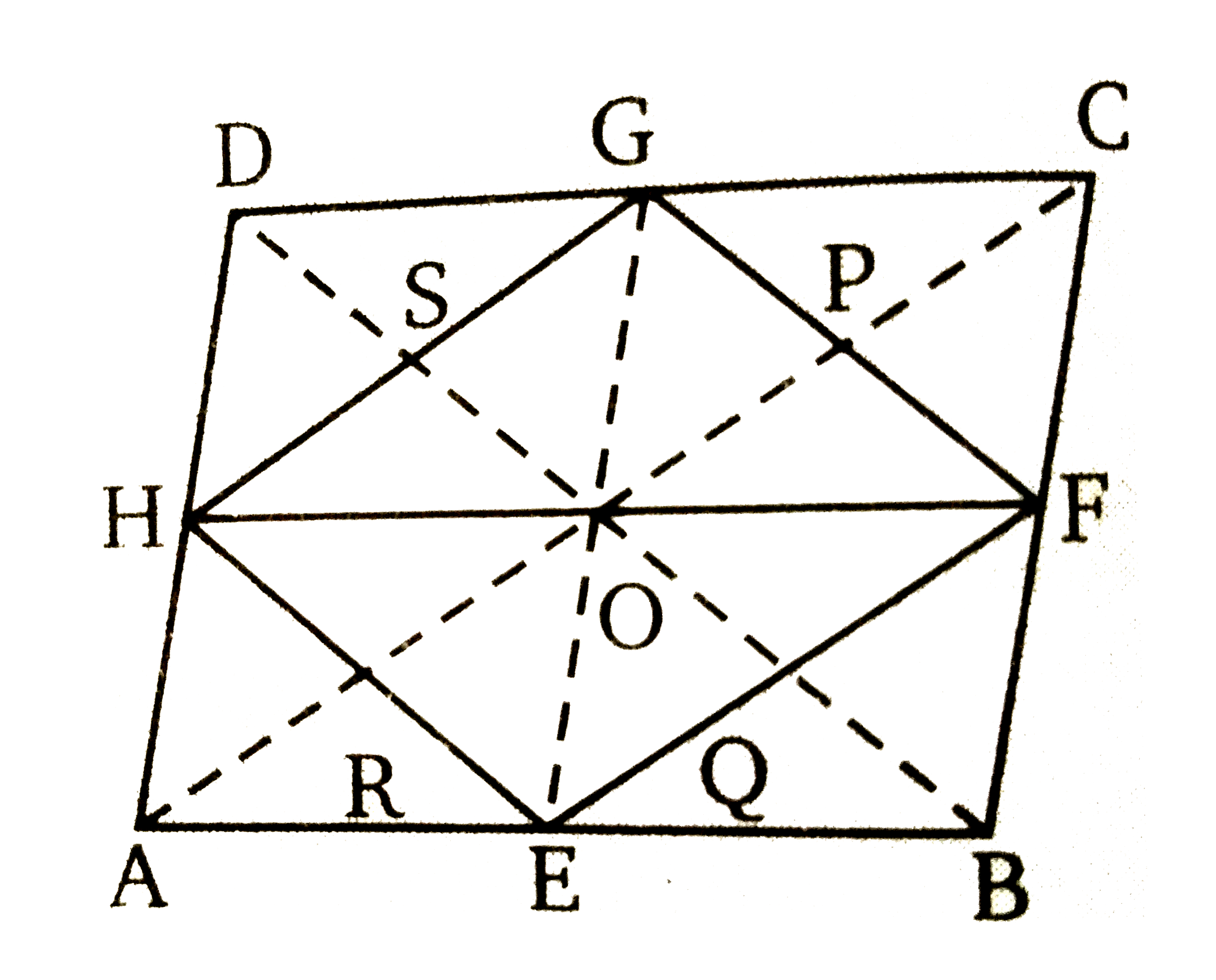
एक समांतर चतुर्भुज $A B C D$ में E,F,G व H क्रमशः भुजाओं $A B, B C, C D$ व $D A$ के मध्य बिंदु हैं। सिद्ध कीजिए कि $E F G H$ एक समांतर चतुर्भुज होगा तथा इसका क्षेत्रफल ABCD के क्षेत्रफल से आधा होगा।

Text Solution

Verified by Experts

(i)रचना: $A C$ व $B D$ को मिलायें
उपपत्‍ति: $F$ व $G$ क्रमशः BC व DC के मध्य बिंदु हैं
$∴ F G ∣ ∣ D B$
इसी प्रकार $E H ∣ ∣ D B$
$∴ E H ∣ ∣ F G$
इसी प्रकार हम सिद्ध कर सकते हैं कि $E F ∣ ∣ G H$
$∴$ चतुर्भुज EFGH एक समांतर चतुर्भुज होगा।
(ii)रचना: $O F, O G, O H, O E$ को मिलायें।
उपपत्‍ति $∵ F$ भुजा CB व O भुजा CA का मध्य बिंदु है।
$∴ F O ∣ ∣ B A$
$\Rightarrow F O ∣ ∣ C G$ व $F O = \frac{1}{2} B A = \frac{1}{2} C D = C G$
अतः चतुर्भुज OFCG एक समांतर चतुर्भुज है।
$∴ O P = P C$ ( $∵$ समांतर चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं।)
अब $Δ O P F$ व $Δ C P F$ का आधार समान है तथा एक शीर्ष उभयनिष्ठ है। इसलिए शीर्षलम्ब भी समान होंगे।
$∴ a r (Δ O P F) = a r (Δ C P F)$
इसी प्रकार $a r (Δ O Q F) = a r (Δ B Q F)$
जोड़ने पर
$a r (Δ O P F) + a r (Δ O Q F) = a r (Δ C P F) + a r (Δ B Q F)$
$\Rightarrow a r (समांतर चतुर्भुज O Q F P) = a r (Δ C P F) + a r (Δ B Q F)$
इसी प्रकार $a r (समांतर चतुर्भुज O P G S) = a r (Δ G P C) + a r (Δ D S G)$
$a r (समांतर चतुर्भुज O S H R) = a r (Δ D S H) + a r (Δ H A R)$
$a r (समांतर चतुर्भुज O R E Q) = a r (Δ A R E) + a r (Δ E Q B)$
उपरोक्त सभी जोड़ने पर
$a r (समांतर चतुर्भुज E F G H) = a r (Δ F C G) + a r (Δ G D H) + a r (Δ H A E) + a r (Δ E B F)$
$= \frac{1}{2} a r (समांतर चतुर्भुज A B C D)$

|

Class 9 MATHS AREA OF PARALLELOGRAMS AND TRIANGLES

Topper's Solved these Questions

Similar Questions

BALAJI PUBLICATION-समांतर चतुर्भुज व त्रिभुज के क्षेत्रफल-स्वमूल्यांकन परीक्षण

Home
Ask Doubt
Profile