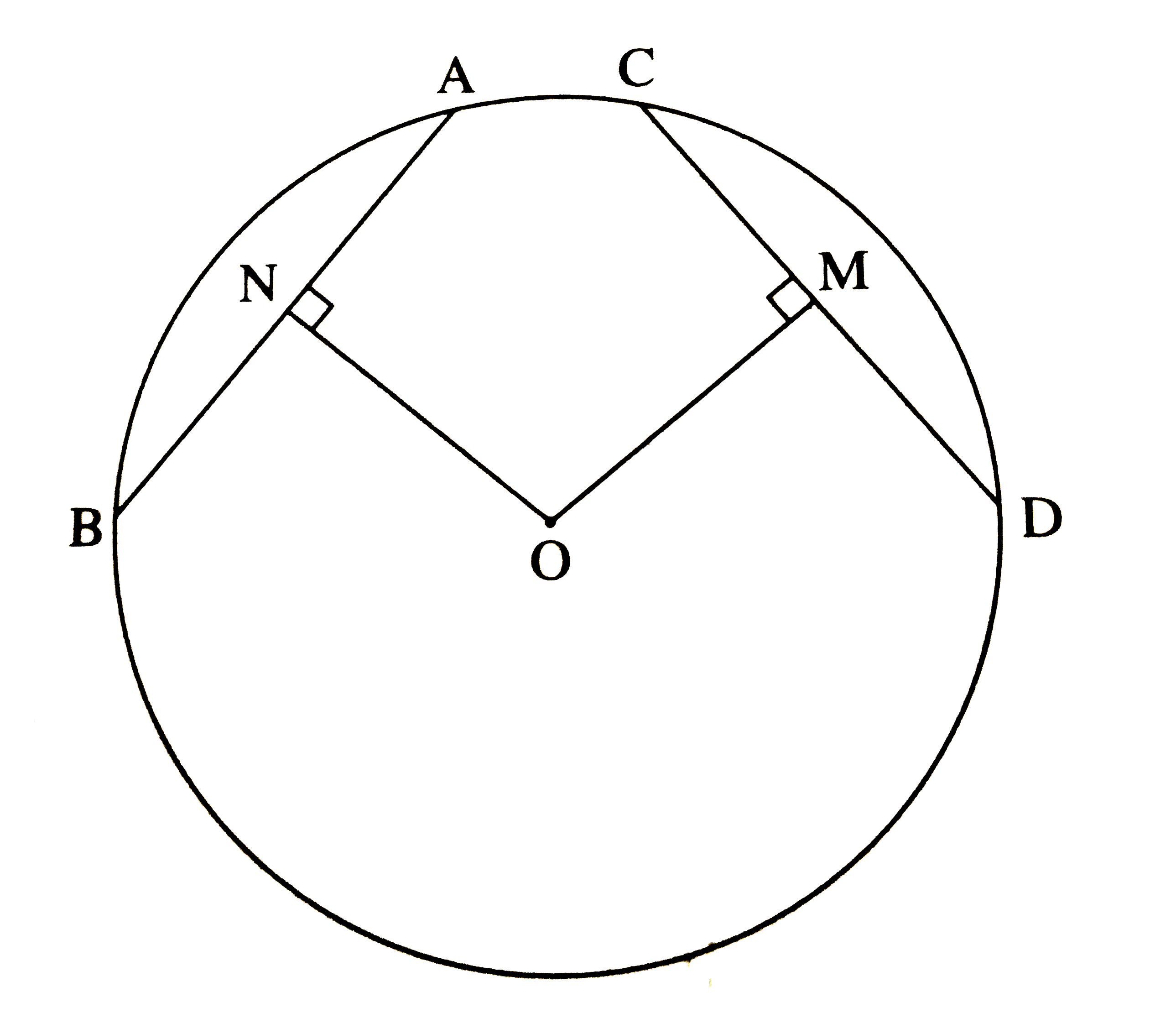
In the figure , O is the center of the circle.chord AB and CD are congruent . If seg ON ⊥ chord AB and seg OM ⊥ chord CD and OM =4cm , then find ON . Justify your answer .
NO =4 cm , congruent chords are equidistant.
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PRACTICE QUESTIONS BASEDEXERCISE - COORDINATE GEOMETRY17videos
PRACTICE QUESTIONS BASED
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PRACTICE QUESTIONS BASEDEXERCISE - TRIGONOMETRY24videos
PRACTICE QUESTIONS BASED
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PRACTICE QUESTIONS BASEDEXERCISE - QUADRILATERALS14videos
PRACTICE QUESTIONS BASED
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PRACTICE QUESTION BASEDEXERCISE - STATISTICS13videos
PRACTICE QUESTION BASED
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY EXERCISE - ASSIGNEMENT 5.412videos
PROBABILITY
Similar Questions
Knowledge Check
- Question 1 - Select One
In the above figure, O is the centre of the circle and AB=CD. If ∠APB=110∘, then find the angle made by the chord CD at the centre.A220∘B110∘C120∘D140∘ - Question 2 - Select One
In a circle with centre P.AB and CD are congruent chords. If ∠PAB=40∘, then ∠CPD=
A40∘B80∘C100∘D50∘
In the adjoining figure, O is the centre of the circle. AB and CD are equal chords.
If ∠AOB=100∘, then find ∠CED.
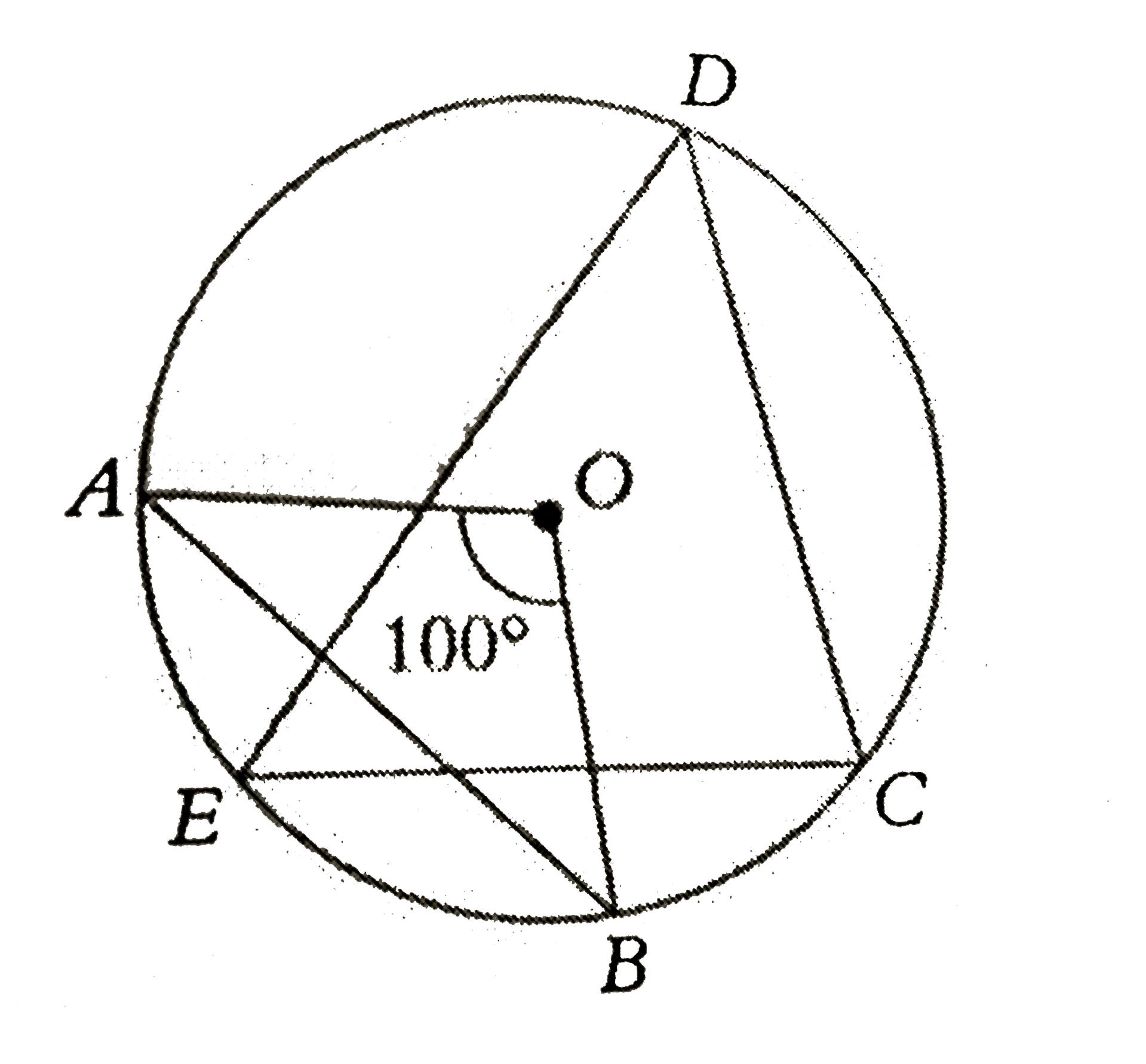View SolutionIn the following figure, O is the centre of the circle. AB and CD are equal chords. If ∠AOB=100∘ , Find the ∠CED.
View Solution
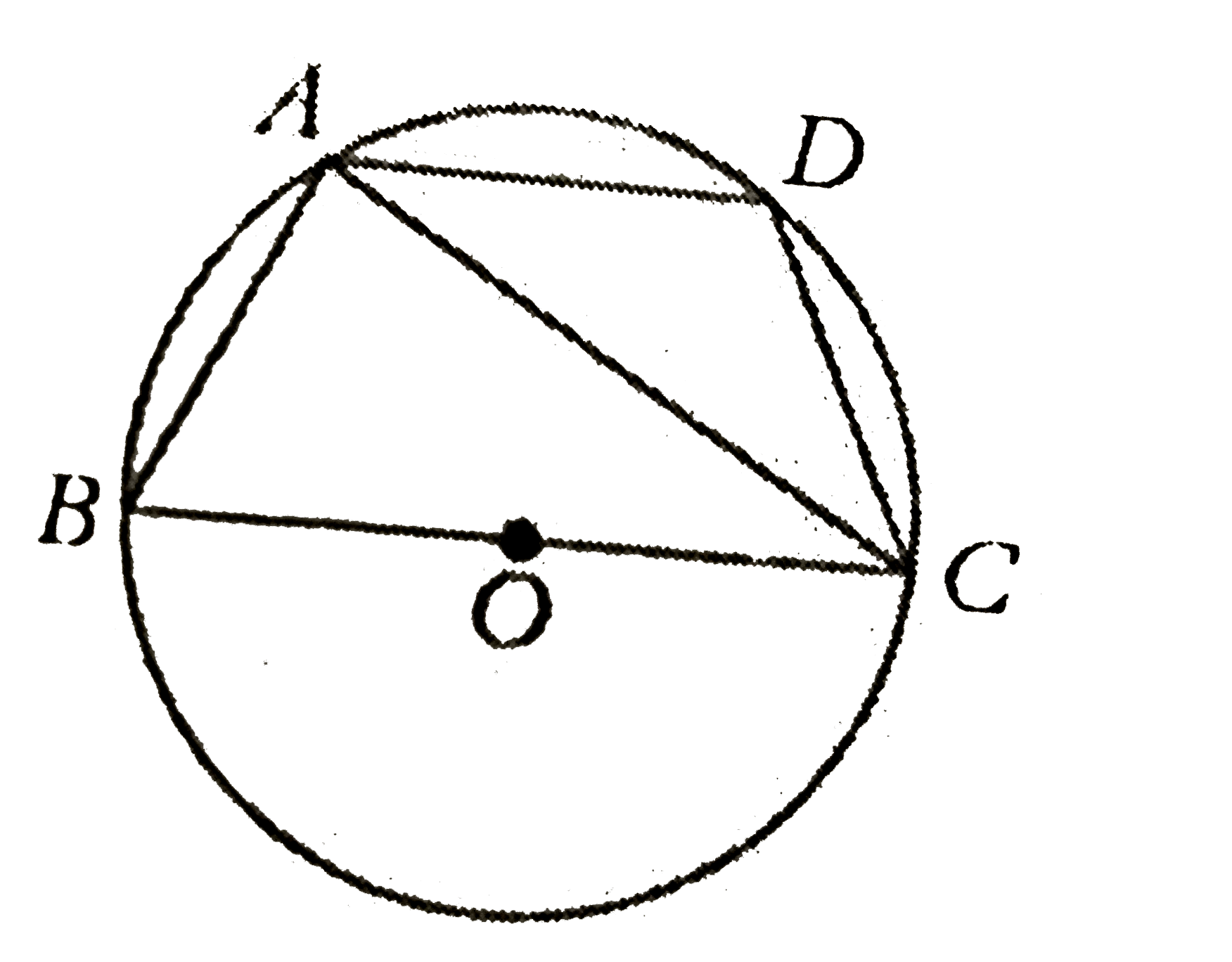
In the above figure, O is the centre of the circle AB,AD and CD are the chords . If ∠ADC=130∘ then fid ∠ACB.View SolutionIn the adjoining figure, 'O' is the centre of the circle. OL and OM are perpendiculars from O to the chords AB and BC respectively. If OL=OM and AB=16cm, then find the length of BC.
View Solution-
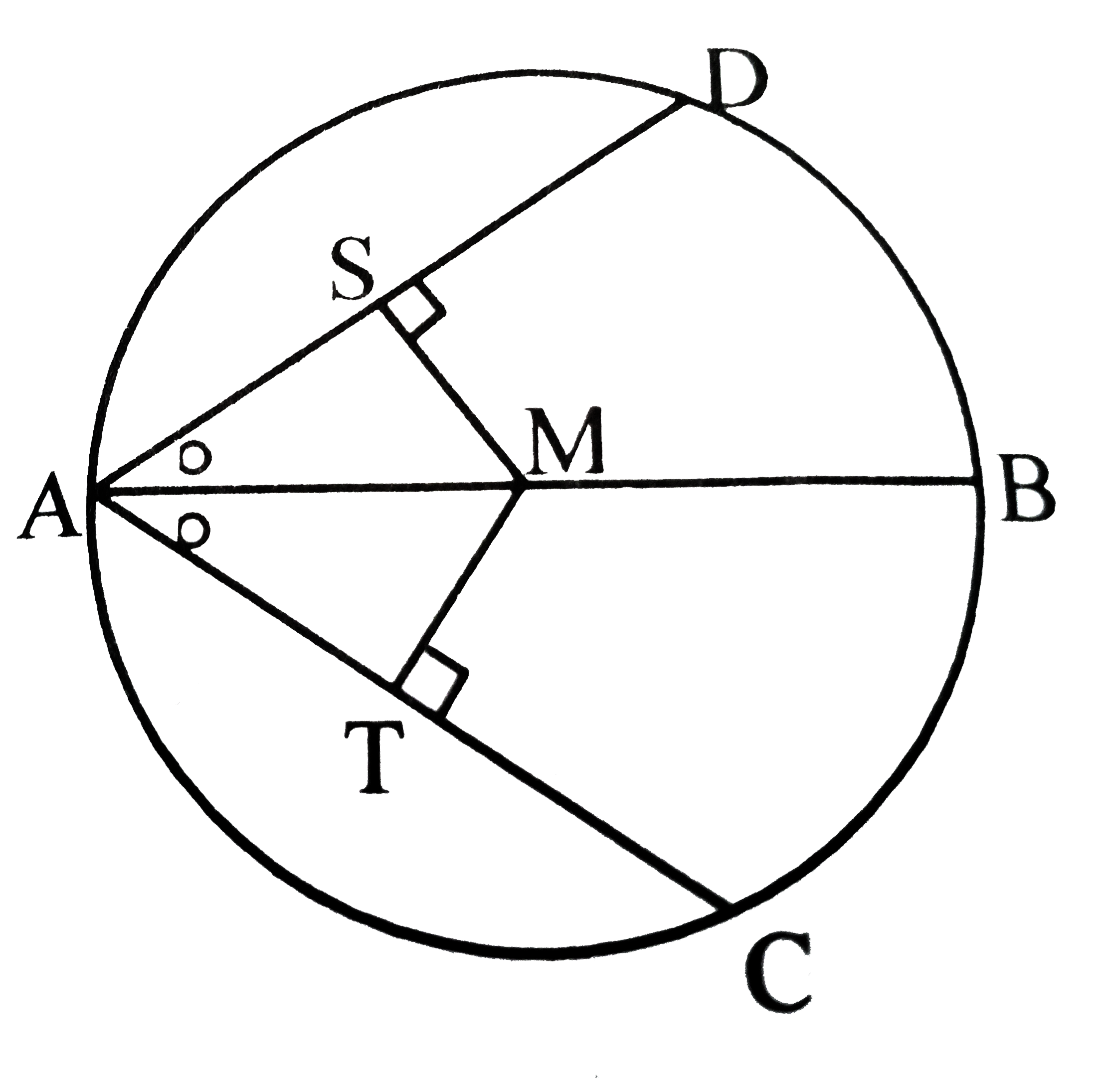
In the above figure, O is the centre of the circle and AB=CD. If ∠APB=110∘, then find the angle made by the chord CD at the centre.View Solution In the adjoining figure, M is the centre of the circle and seg AB is a diameter. Seg MS⊥ chord AD, seg MT ⊥ chord AC, ∠DAB≅∠CAB.
Prove that : chord AD≅ chord AC.
View Solution