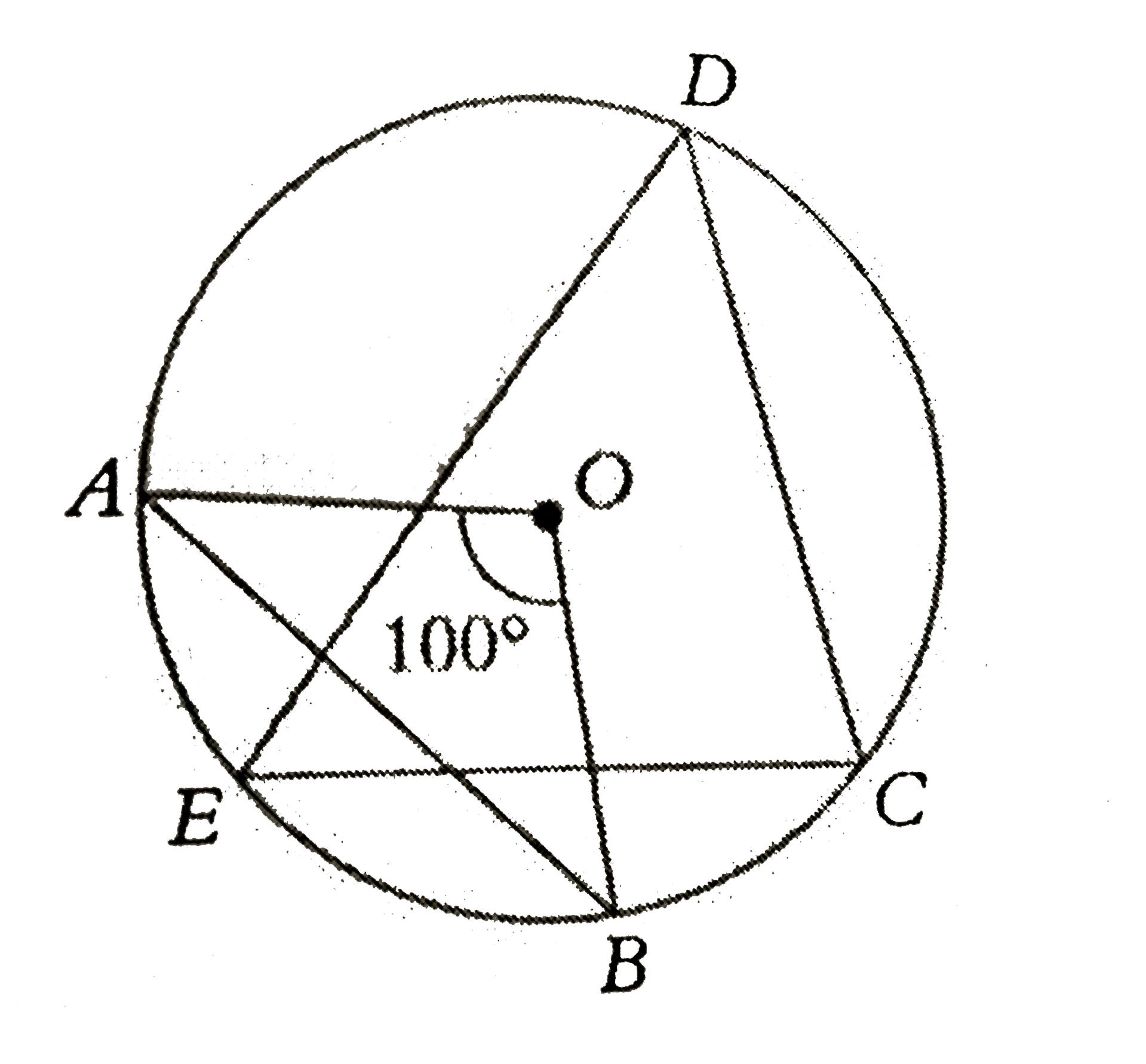In the adjoining figure, 'O' is the centre of the circle. OL and OM are perpendiculars from O to the chords AB and BC respectively. If OL=OM and AB=16cm, then find the length of BC.

The correct Answer is:16 cm
NA
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10c
20 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )
5 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
Knowledge Check
In the adjoining figure O is the centre of the circle . If chord AB=2 cm radius OA=2 cm, then find the value of ∠ACB.
 A=60∘B=45∘C=30∘D=50∘
A=60∘B=45∘C=30∘D=50∘In the adjoining figure D is the midpoint of BC of a ΔABC,DMandDN are the perpendiculars on AB and AC respectively and DM=DN, then the ΔABC is :
 Aright angledBisoscelesCequilateralDscalene
Aright angledBisoscelesCequilateralDscalene
.In given figure OC is perpendicular segment drawn from centre O to chord AB. If OB=5 cm and OC= 3cm then find the length of AB
View SolutionIn the adjoining figure, O is the centre of the circle and AB is its diameter. If AC=8 cm and BC= 6cm, then find the radius of the circle.

View SolutionIn the adjoining figure, O is the centre of a circle in which AB and CD are two diameters. Prove that AC| |BD and AD| |BC. If ∠OBD=50∘, then find the value of ∠AOC.

View SolutionIn the adjoining figure, O is the centre of the circle. If the chord AB is equal to the radius of the circle, then find the value of ∠ADB.

View Solution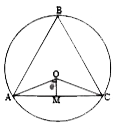
In the figure given above, O is the centre of the circle OA = 3 cm, AC = 3 cm and OM is perpendicular to AC. What is ∠ABC equal to ?
View SolutionIn the given figure, O is the centre of the circle. Its two chords AB and CD intersect each other at the point p within the circle. If AB=15cm,PB=9cm, then find the length of PD.
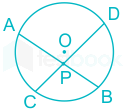
View Solution