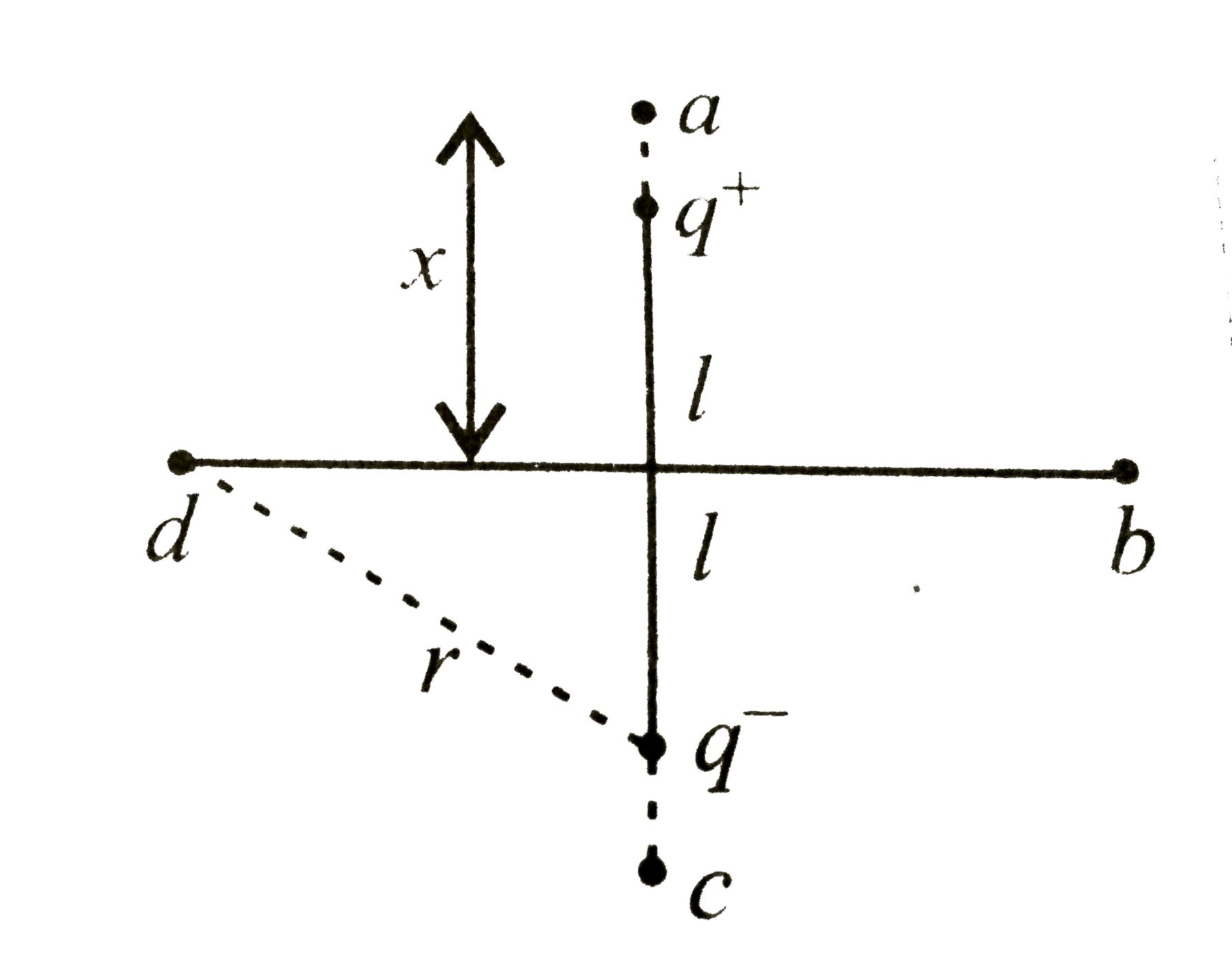
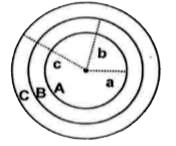
Four points a, b, c and d are set at equal distance from the centre of a dipole as shown in the figure. The magnitudes of electrostatic potential Va,Vb,VcandVd would satisfy which of the following relation?

Va>Vb>Vc>Vd
Va>Vb>=Vd>Vc
Va=Vc>Vb=Vd
Vb=Vd>Va>Vc
The correct Answer is:C
Va due to q+=14πε0.1(x−l)
Va due to q−=−14πε0.q(x+1)
∴Va total=q4πε0.{1(x−l)−1(x+l)}
Va=q4πε0.2l(x2−l2)⇒Va=2lq4πε0x2 (if l lt lt x)=p4πε0x2
Vc=q4πε0.{1(x−l)+1(x+l)}=-2lq4πε0.(x2)
Vd=+q4πε0.{1r−1r} due to +q and -q =0
Vb=0
∴Va=Vc>Vb=Vd
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTIPSCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Potential Due To A System Of Charges
7 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTIPSCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Equipotential Surfaces
9 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTIPSCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Potential Due To A Point Charge
7 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT FINGERTIPSCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Assertion And Reason
15 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTIPSCHAPTER - MAGNETISM AND MATTER EXERCISE - Assertion And Reason
15 Videos
Similar Questions
Four points a, b, c and d are set at equal distance from the centre of a dipole as shown in the figure. The magnitudes of electrostatic potential Va,Vb,VcandVd would satisfy which of the following relation?

View SolutionFind the potential difference VA−CB for the circuit shown in the figure .
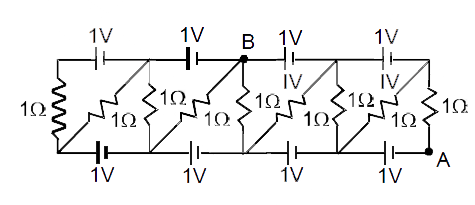
View Solution
Knowledge Check
The potential difference (VA−VB) between the point A and B as shown in the figure is
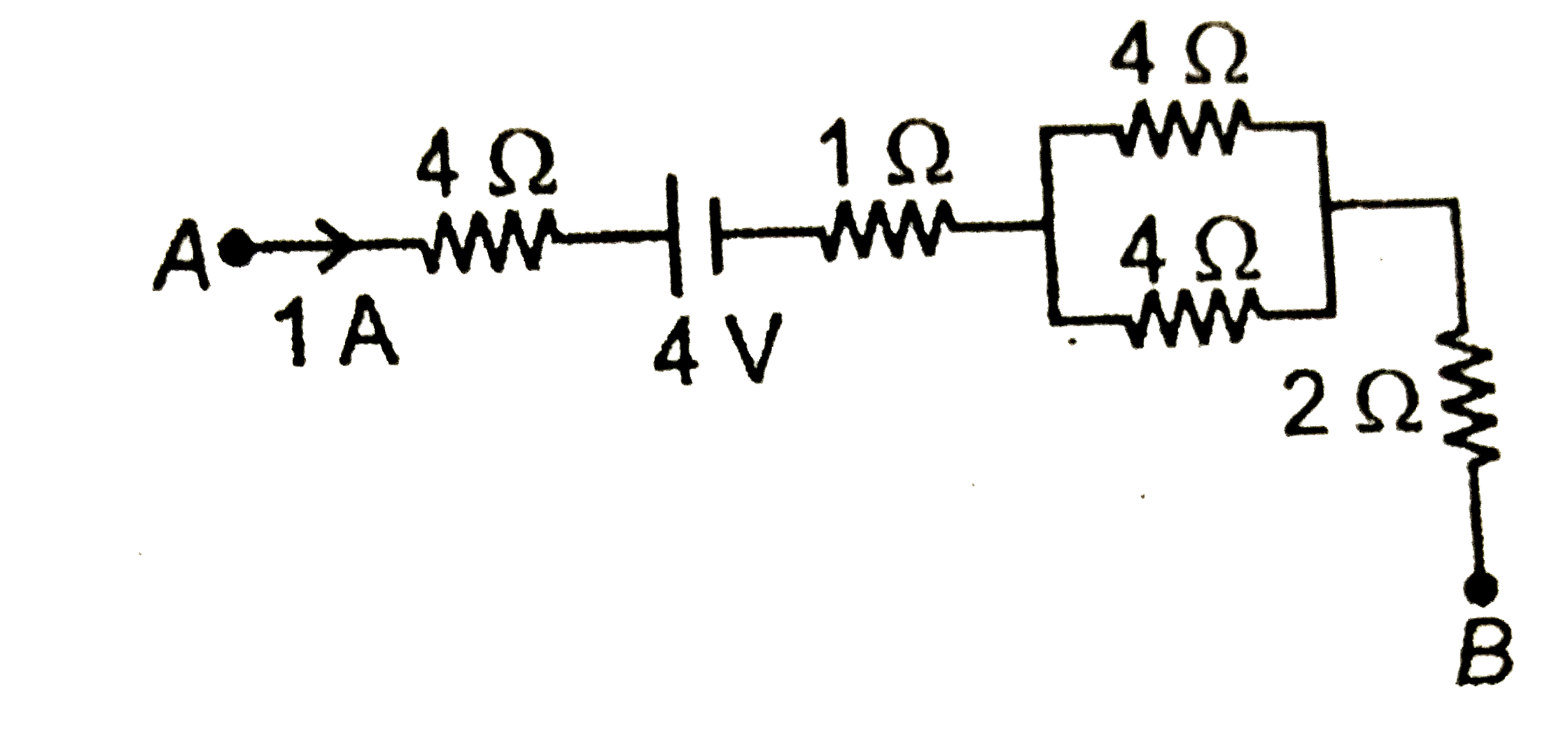 A9VB8VC15VD13V
A9VB8VC15VD13VIn the circuit shown in the figure, the ratio of VB as VC is
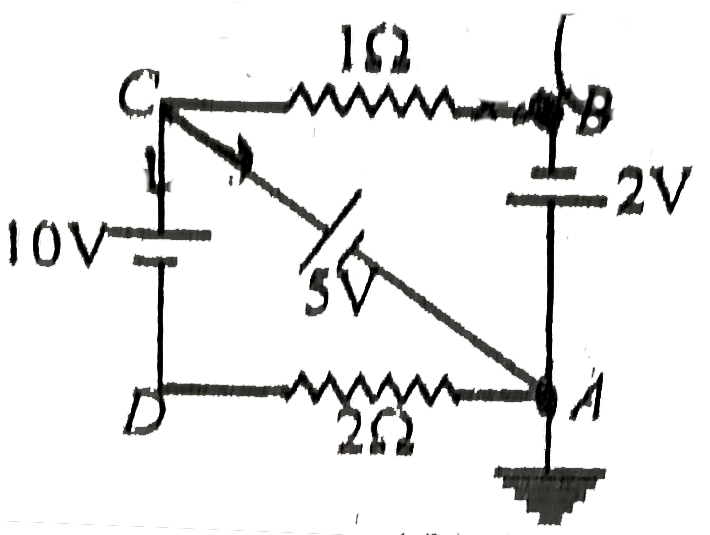 A−2/5B−5/2C1D1/3
A−2/5B−5/2C1D1/3
A dipole of dipole moment →p=pˆi is kep at the centre of a circle of radius r as shown in the figure. The radius of the circle is very large in comparison to the distance between the two charges of the dipole. A & B are two points on the axis and C & D are two points on the equitorial line of the dipole if VA,VB,VC and VD are potentials at A,B,C and D respectively then, which of the following is correct?AVA−VB=0,VA−VD=2kpr2BVA−VB=2kpr2,VA−VD=kpr2CVA−VB=0,VA−VD=kpr2DVA−VB=2kpr2,VA−VD=2kpr2
Find the equivalent resistance of the network shown in the figure between the points A and B if
(i) VA>VB (ii) VA<VB

View Solution
A particle is given velocity v0 at point A as shown in the figure. Find the speed of particle at point B,C and D
View SolutionFind the potential difference Va−Vb between the points a and b shown in each part of the figure.

View SolutionFind the potential difference Va−Vbin the circutis shown in figure

View SolutionThree concentric charged metallic spherical shells A, B and C have radii a,b and c, charge densities σ,−σ and σ and potentials VA,VB and VC respectively. Then which of the following relations is correct?
View Solution
