A galvanometer has a current sensitivity of 1 mA per division. A variable shunt is connected across the galvanometer and the combination is put in series with a resistance of 500Ω and cell of internal resistance 1Ω. It gives a deflection of 5 division for shunt of 5 ohm and 20 division for shunt of 25 ohm. The emf of cell is
47.1 V
57.1 V
67.1 V
77.1 V
The correct Answer is:A
Here, I=ER+r+GSG+S and Ig=ISG+S
Ig=E(R+r)+GSG+S×SG+S
∴Ig=ES(R+r)(G+S)+GS
For S=5ohm,Ig=5×10−3A
and for S=25ohm,Ig=20×10−3A
Hence, 5×10−3=E×5501(G+5)+5G...........(i)
and 20×10−3=E×25501(G+25)+25G.........(ii)
Dividing and solving, G= 88.2Ω
From (i), we get
E=10−3[501(88.2+5)+5×88.2]=47.1 volt
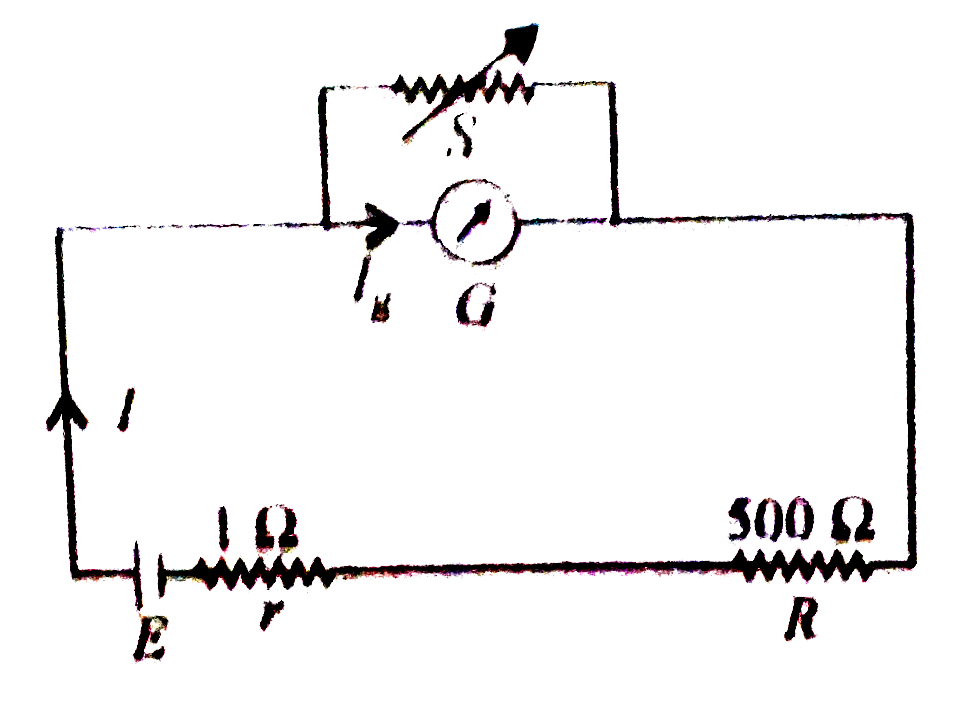
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTIPSCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - NCERT Exemplar
6 Videos
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTIPSCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - Assertion And Reason
15 Videos
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTIPSCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - The Moving Coil Galvanometer
16 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTIPSCHAPTER - MAGNETISM AND MATTER EXERCISE - Assertion And Reason
15 Videos
- NUCLEIBOOK - NCERT FINGERTIPSCHAPTER - NUCLEIEXERCISE - Assertion And Reason
15 Videos
Similar Questions
A variable shunt is connected across the galvanometer which has a current sensitivity of 1mA per division and the combination is put in series with a resistance of 500Ω and cell of internal resistance 2Ω?. For a shunt of 5 ohm, it gives a deflection of 5 division and for shunt of 30 ohm, it gives 25 division. The emf of cell is-----V.
View SolutionA galvanometer having 50 divisions provided with a variable shunt S is used to measure the current when connected in series with a resistance of 90Ω and a battery of internal resistance 10Ω. It is observed that when the shunt resistances are 10Oemga and 50Ω, the deflections are, respectively, 9 and 30 divisions. What is the resistance of the galvanometer
View Solution
Knowledge Check
A galvanometer has a current sensitivity of 1 mA per division.A variable shunt is connected across the galvanometer and the combination is put in series with a resistance of 500 Ω and cell of intemal resistance 1Ω. It gives a deflection of 5 division for shunt of 5 ohm and 20 division for shunt of 25 ohm. The emf of the cell is
A47.1VB57.1VC67.1VD77.1VA galvanometer has a sensitivity of 60 division/ampere. When a shunt is used its sentivity becomes 10 divisions/ampere. What is the value of shunt used if the resistance of the galvanometer is 20Ω?
A2ΩB3ΩC4ΩD6ΩA galvanometer has a current sensitivity of 5 divisions per milliampere and voltage sensitivity of 1 division per millivolt. The galvanometer has 30 divisions and it is to be used as an ammeter to read 6 A. This requires a shunt of value
A5999ΩB1333ΩC1111ΩD7999Ω
A galvanometer having 50 divisions provided with a variable shunt S is used to measure the current when connected in series with a resistance of 90Ω and a battery of internal resistance 10Ω. It is observed that when the shunt resistances are 10Oemga and 50Ω, the deflections are, respectively, 9 and 30 divisions. What is the resistance of the galvanometer
View SolutionThe combinant resistance of a galvanometer of resistance500Ωand its shunt is 25Ω. What is the value of the shunt?
View SolutionThe deflection in a galvanometer decreases to 1/5th of the original deflectioon, if it is shunted by a resistance of 5Ω. The resistance of the galvanometer is
View SolutionWhen a moving coil galvanometer is shunted with a resistance of 10Ω,the deflection in the galvanometer reduces from 30 divisions to 6 divisions. The resistance of the galvanometer is
View SolutionThe Senstivity of a galvanometer is 60div/Ampere. When a shunt is used, its sensitivity becomes 10div/Ampere. If the resistance of the galvanometer is20Ω,then the value of the shunt used is
View Solution
