Calculate the period of oscillations of block of mass m attached with a set of springs as shown
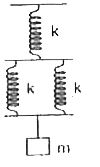
2π√m3k
2π√3m2k
2π√2m3k
2π√3km
The correct Answer is:B
Step by step video, text & image solution for Calculate the period of oscillations of block of mass m attached with a set of springs as shown by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-I) (Assertion Reasoning type)3videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)20videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Subjective) (Level-II & III)13videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I20videos
SEMICONDUCTOR AND DEVICE
- BOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS747videos
TEST PAPERS
Similar Questions

The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks isView Solution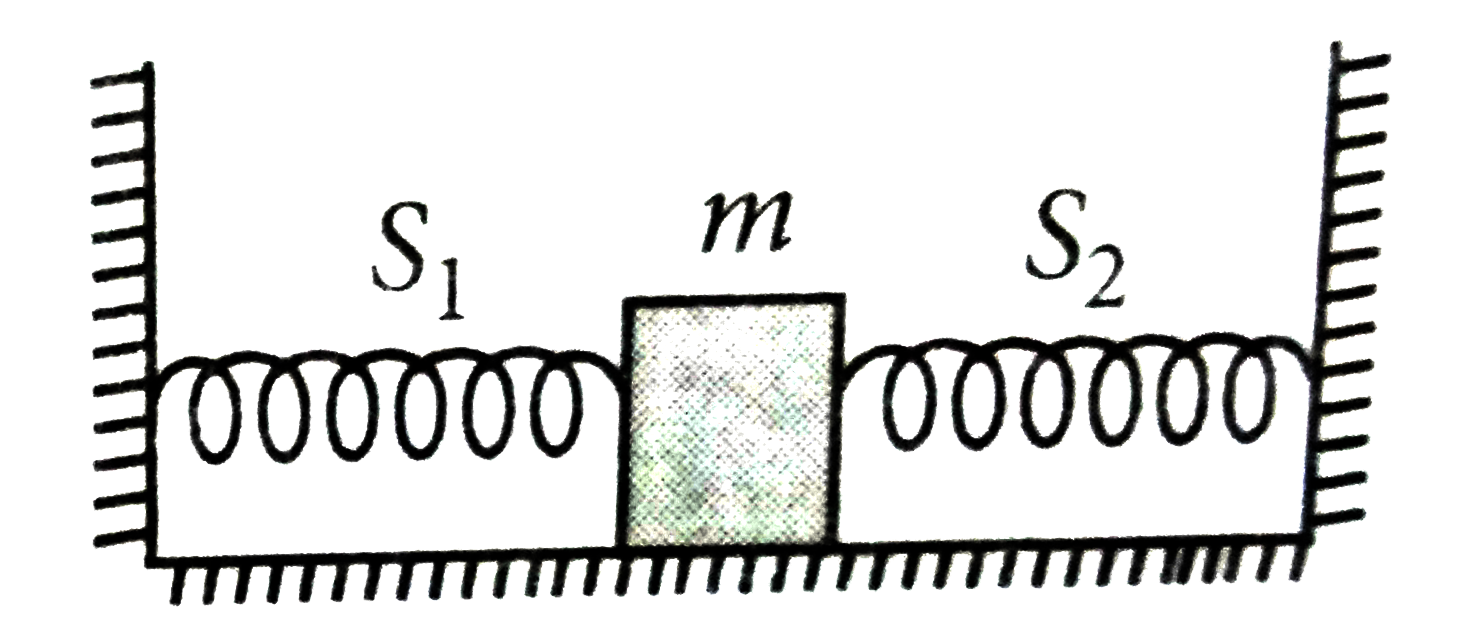
When a mass m is connected individually to two springs S1andS2, the oscillation frequencies are υ1andυ2. If the same mass is attached to the two springs as shown in figure, the oscillation frequency would beView Solution
Knowledge Check
- Question 1 - Select One
Find the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
 A2π√mkBπ√mkC4π√mkD2π√m2k
A2π√mkBπ√mkC4π√mkD2π√m2k - Question 2 - Select One
The graph between period of oscillation (T) and mass attached (m) to a spring will be
A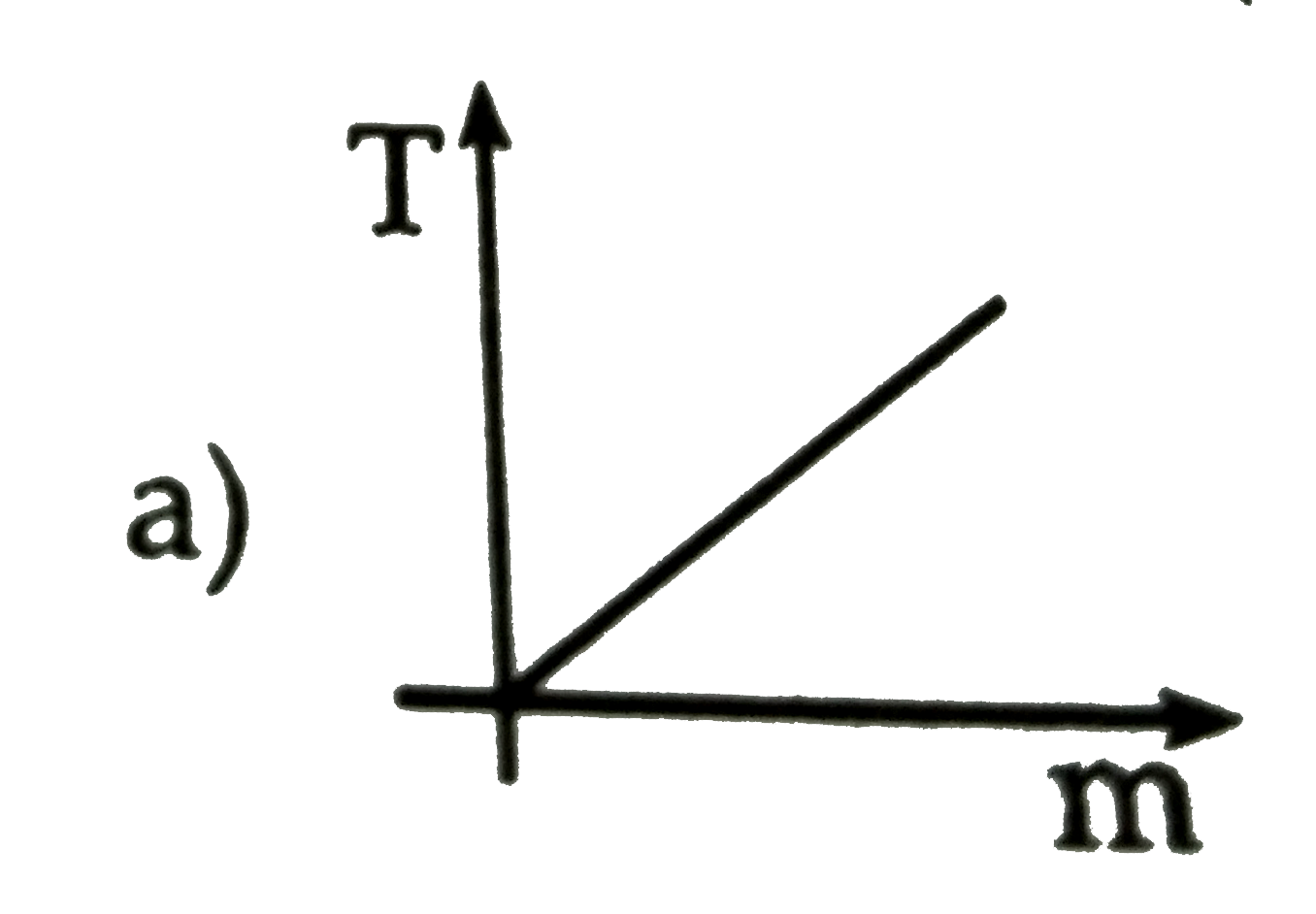 B
B C
C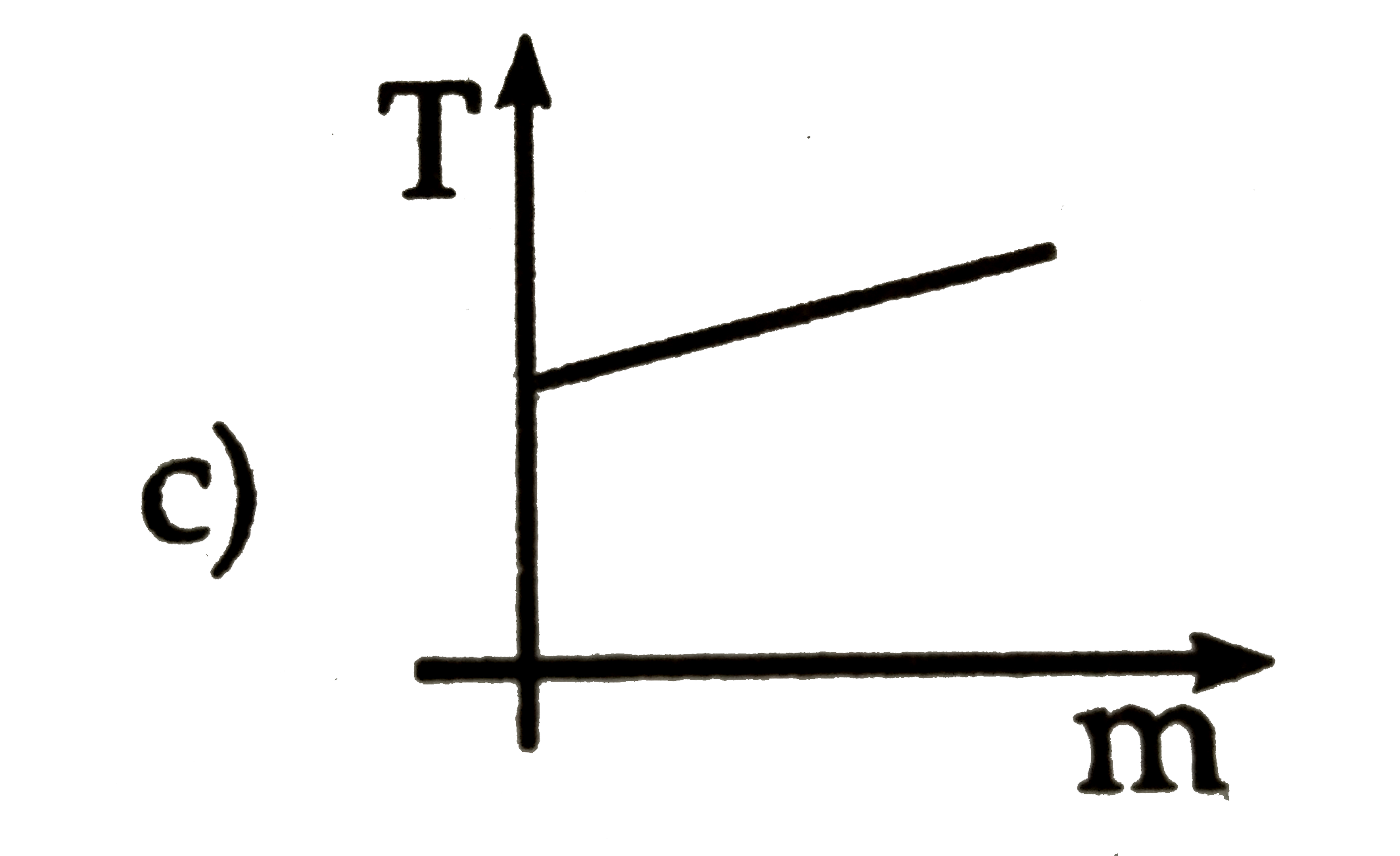 D
D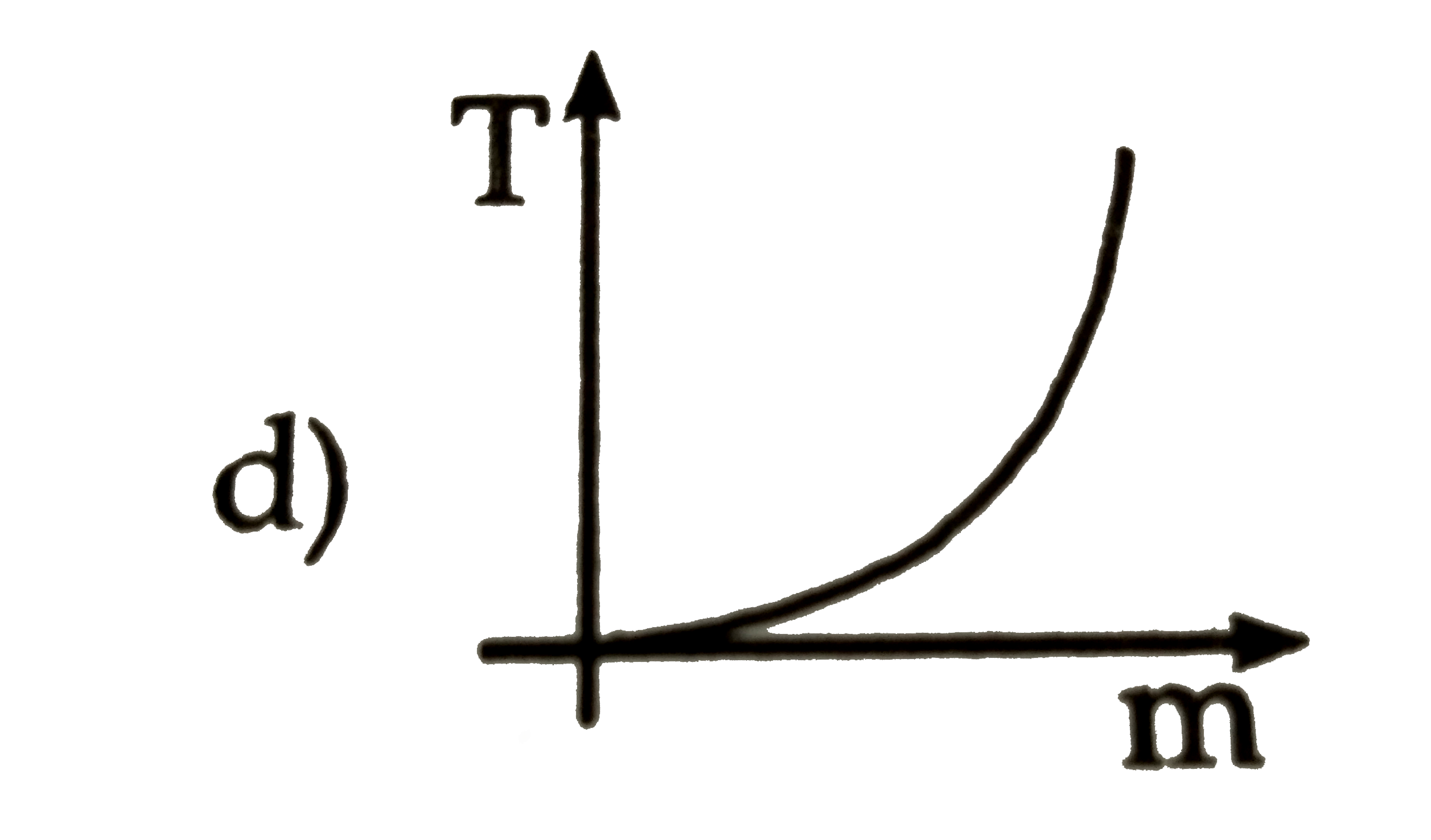
- Question 3 - Select One
The time period of oscillations of a block attached to a spring is t1. When the spring is replaced by another spring, the time period of the block is t2. If both the springs are connected in series and the block is made to oscillate using the combination, then the time period of the block is
AT=t1+t2BT2=t21+t22CT−1=t−11+t−12DT−2=t−21+t−22
A mass m is suspended from a weightless spring. The time period of oscillation of mass is 3 s . Calculate the value of m if on suspending an additional mass of 3kg, time period increases by 2 s.
View SolutionThree arrangements are shown in figure.
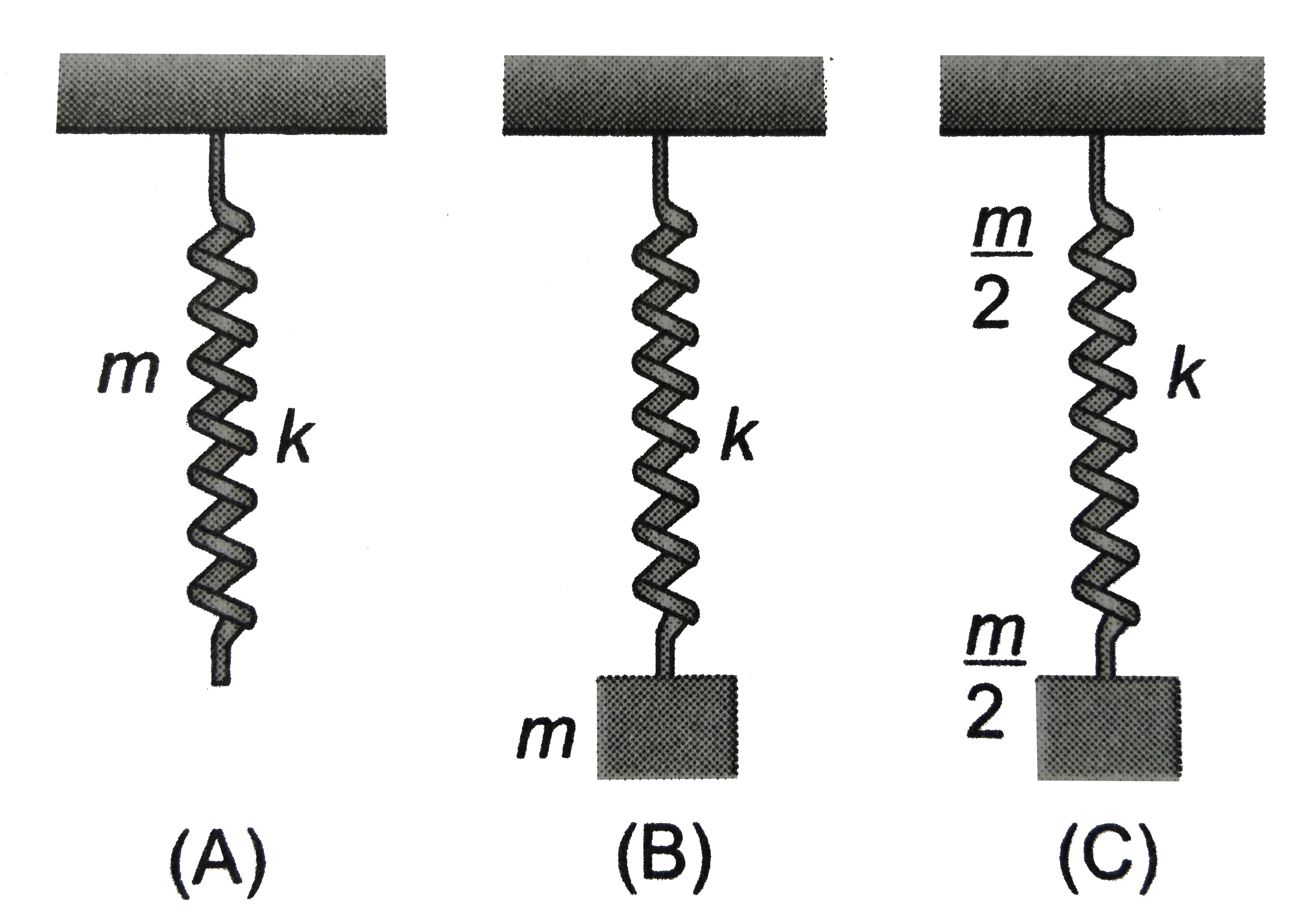
(a) A spring of mass m and stiffness k
(b) A block of mass m attached to massless spring of stiffness k
( c) A block of mass m2 attached to a spring of mass m2 and stiffness k
If T1, T2 and T3 represent the period of oscillation in the three cases respectively, then identify the correct relation.View SolutionOn a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has force constant K , the period of oscillation of the body (assuming the springs as massless) is
 View Solution
View SolutionOn a smooth inclined plane a body of mass M is attached between two springs. The other ends of the spring are fixed to ffirm supports. If each spring has a force constant k, the period of oscillation of the body is: (assuming the spring as massless)
 View Solution
View SolutionA block of mass m is placed on a smooth block of mass M=m with the help of a spring as shown in the figure. A velocity v0 is given to upper block when spring is in natural length. Find maximum compression in the spring.
 View Solution
View Solution

