In ΔABC,∣∣¯¯¯¯¯¯CB∣∣=a,∣∣¯¯¯¯¯¯CA∣∣=band∣∣¯¯¯¯¯¯AB∣∣=c.CD is the median through the vertex C. Then ¯¯¯¯¯¯CA.¯¯¯¯¯¯CD=
Step by step video & image solution for In DeltaABC, |bar(CB)| = a, |bar(CA)| = b and |bar(AB)| =c. CD is the median through the vertex C. Then bar(CA).bar(CD)= by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
If G is the centroid of Δ ABC, then ¯¯¯¯¯¯CA+¯¯¯¯¯¯CB =
A3 ¯¯¯¯¯¯GCB3 ¯¯¯¯¯¯CGC3 ¯¯¯¯¯¯ABD3 ¯¯¯¯¯¯GAIf AD , BE and CF are medians of ΔABC, then ¯¯¯¯¯¯AD+¯¯¯¯¯¯BE+¯¯¯¯¯¯CF =
A¯¯¯¯¯¯BD+¯¯¯¯¯¯EA+¯¯¯¯¯¯FBB0C¯¯¯¯¯¯AE+¯¯¯¯¯¯DB+¯¯¯¯¯¯FAD¯0If ABCD is a square, then
¯¯¯¯¯¯AB+2¯¯¯¯¯¯BC+3¯¯¯¯¯¯CD+4¯¯¯¯¯¯DA =A4 ¯¯¯¯¯¯ACB3 ¯¯¯¯¯¯ACC2 ¯¯¯¯¯¯CAD¯¯¯¯¯¯AC
In the given figure ¯¯¯¯¯¯AB=¯¯¯¯¯¯BC and ¯¯¯¯¯¯AC=¯¯¯¯¯¯CD if ∠BAD=y and ∠ADB=x then ∠y=
View Solution
In the figure above, ¯¯¯¯¯¯AB||¯¯¯¯¯¯CD. Find the value of x.
View Solution
In the figure above, ¯¯¯¯¯¯AB||¯¯¯¯¯¯CD. Find the value of x.
View SolutionIf ABCD is a square then,
2¯¯¯¯¯¯AB+4¯¯¯¯¯¯BC+5¯¯¯¯¯¯CD+7¯¯¯¯¯¯DA=
View SolutionIn the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
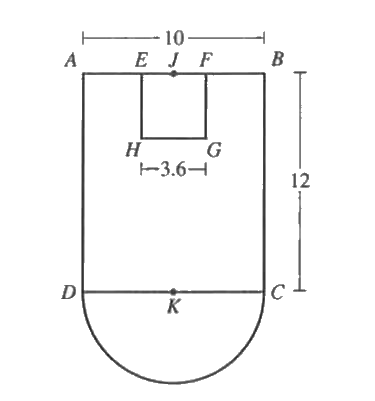
What is the length, in meters, of are ¯¯¯¯¯¯CD?
View Solution
