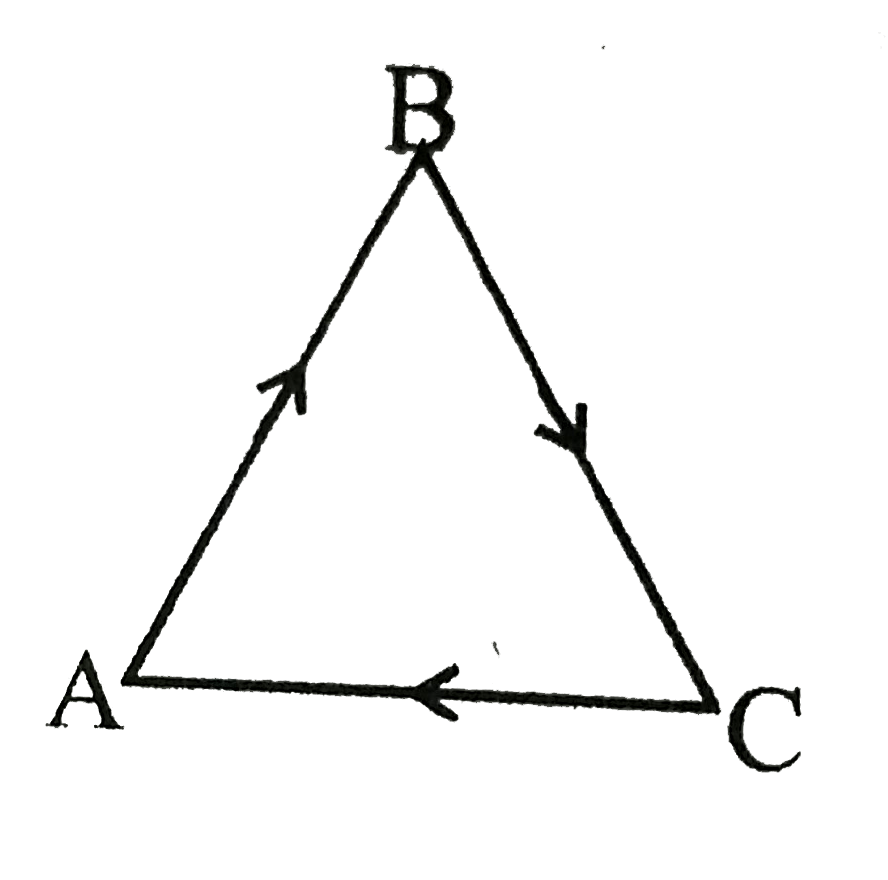
ABC is an equilateral triangle of side ‘a'. Then ¯¯¯¯¯¯AB.¯¯¯¯¯¯BC+¯¯¯¯¯¯BC.¯¯¯¯¯¯CA+¯¯¯¯¯¯CA.¯¯¯¯¯¯AB=
Step by step video & image solution for ABC is an equilateral triangle of side ‘a'. Then bar(AB).bar(BC) +bar(BC).bar(CA)+ bar(CA).bar(AB) = by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
If ABCDE is a pentagon, then ¯¯¯¯¯¯AB+¯¯¯¯¯¯AE+¯¯¯¯¯¯BC+¯¯¯¯¯¯DC+¯¯¯¯¯¯ED=
A¯¯¯¯¯¯ACB2¯¯¯¯¯¯ACC2¯¯¯¯¯¯ADD3¯¯¯¯¯¯AD - Question 2 - Select One
If ABCDE is a regular penatagon then :
¯¯¯¯¯¯AB+¯¯¯¯¯¯BC+¯¯¯¯¯¯AD+¯¯¯¯¯¯ED+¯¯¯¯¯¯AE=A¯¯¯¯¯¯AC−2¯¯¯¯¯¯DCB3¯¯¯¯¯¯AC−2¯¯¯¯¯¯DCC¯¯¯¯¯¯CA−¯¯¯¯¯¯DCD3¯¯¯¯¯¯AC−¯¯¯¯¯¯DC - Question 3 - Select One
If ABCD is a square, then
¯¯¯¯¯¯AB+2¯¯¯¯¯¯BC+3¯¯¯¯¯¯CD+4¯¯¯¯¯¯DA =A4 ¯¯¯¯¯¯ACB3 ¯¯¯¯¯¯ACC2 ¯¯¯¯¯¯CAD¯¯¯¯¯¯AC
A,B,C,D are four points in space and ∣∣¯¯¯¯¯¯ABׯ¯¯¯¯¯CD+¯¯¯¯¯¯BCׯ¯¯¯¯¯AD+¯¯¯¯¯¯CAׯ¯¯¯¯¯BD∣∣=λ (area ΔABC) then value of λ is _____
View SolutionABC is an equilateral triangle. P and Q are two points on ¯¯¯¯¯¯AB and ¯¯¯¯¯¯AC respectively such that ¯¯¯¯¯¯PQ∣∣¯¯¯¯¯¯BC. If ¯¯¯¯¯¯PQ=5cm, then area of ΔAPQ is :
View SolutionIf ABCD is a square then,
2¯¯¯¯¯¯AB+4¯¯¯¯¯¯BC+5¯¯¯¯¯¯CD+7¯¯¯¯¯¯DA=View SolutionIf D is the mid -point of side AB of ΔABC, then ¯¯¯¯¯¯AB+¯¯¯¯¯¯BC+¯¯¯¯¯¯AC=
View SolutionΔABC is an isosceles triangle and ¯¯¯¯¯¯AB=¯¯¯¯¯¯AC=2aunit, ¯¯¯¯¯¯BC = a unit. Draw AD⊥BC, and find the length of ¯¯¯¯¯¯AD .
View Solution