Base of a triangle is 9 and height is 5. Base of another triangle is 10 and height is 6. Find the ratio of areas of these triangles.
Let the base height and area of the first triangle be b1,h1 and A1 respectively. Let the base, height and area of the second triangle be b2,h2 and A2 respectively.
b1=9,h1=5,b2=10 and h2=6.
The ratio of areas of two triangles is equal to the ratio of the products of their bases and corresponding heights.
A1A2=b1×h1b2×h2
∴A1A2=9×510×6∴A1A2=34
The ratio of the areas of the triangles is 3:4.
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - CHALLENGING QUESTIONS8videos
SIMILARITY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - MCQ TYPE15videos
SIMILARITY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - 2.5 (4 mark each)3videos
SIMILARITY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNEMENT 2.48videos
QUADRATIC EQUATIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - STATISTICSEXERCISE - EXAMPLES FOR PRACTICE (MCQs)35videos
STATISTICS
Similar Questions
The height of a triangle is 2 cm less than twice its base. If the base of the triangle is 6 cm, then what is the area of the triangle?
View SolutionThe ratio of the areas of two triangles with equal height is 3 : 4. Base of the smaller triangle is 15 cm. Find the corresponding base of the large triangle.
View Solution
Knowledge Check
- Question 1 - Select One
The base of a triangle is 14 cm and its height is 8 cm. The area of the triangle is
A112cm2B56cm2C122cm2D66cm2 - Question 2 - Select One
The base of a triangle is 12cm and height is 8cm then area of triangle is
A48cm2B24cm2C96cm2D56cm2 - Question 3 - Select One
The base of a triangle is 15cm and height is 12cm. The height of another triangle of double the area having the base 20cm is (a) 8cm (b) 9cm (c) 12.5cm (d) 18cm
A8 cmB9 cmC12.5 cmD18 cm
The height of a triangle is x4+y4 and its base is 14xy. Find the area of the triangle.
View SolutionThe height of a triangle is 10 cm and its base is 5 cm. Find its area
View SolutionThe given figure shows a triangle of 18 m height. The base of the triangle is 20 m long.
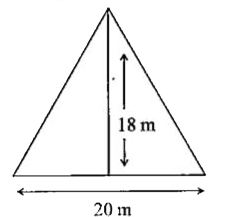
What is the area of the triangle?View SolutionRatio of areas of two triangles with equal height is 2:3. If base of the smaller triangle is 6 cm, the what is the corresponding base of the bigger triangle?
View SolutionEach of the equal sides of an isosceles measures 2 cm more than its height , and the base of the triangle measures 12 cm. Find the area of the triangle.
View Solution

