The corresponding medians of two similar triangles are in the ratio 4:7. Let their respective areas be A1 and A2.A1:A2=…
0.70069444444444
0.17152777777778
0.29444444444444
2.0527777777778
The correct Answer is:A
NA
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - SUBJECTIVE TYPE20videos
SIMILARITY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - CHALLENGING QUESTIONS8videos
SIMILARITY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNEMENT 2.48videos
QUADRATIC EQUATIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - STATISTICSEXERCISE - EXAMPLES FOR PRACTICE (MCQs)35videos
STATISTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
A uniform magnetic field passes through two areas, A1 and A2. The angles between the magnetic field and the normals of areas A1 and A2 are 30.0° and 60.0°, respectively. If the magnetic flux through the two areas is the same, what is the ratio A1/A2?
A0.577B1C0.816D1.23 - Question 2 - Select One
Let A0A1A2A3A4A5 be a regular hexagon inscribed in a circle of unit radius. Then the product of the lengths of the line segments A0A1,A0A2andA0A4 is
A34B3√3C3D√32 - Question 3 - Select One
The spectrum of a black body at two temperatures 27∘C and 327∘C is shown in the figure. Let A1 and A2 be the areas under the two curves respectively. Find the value of A2A1
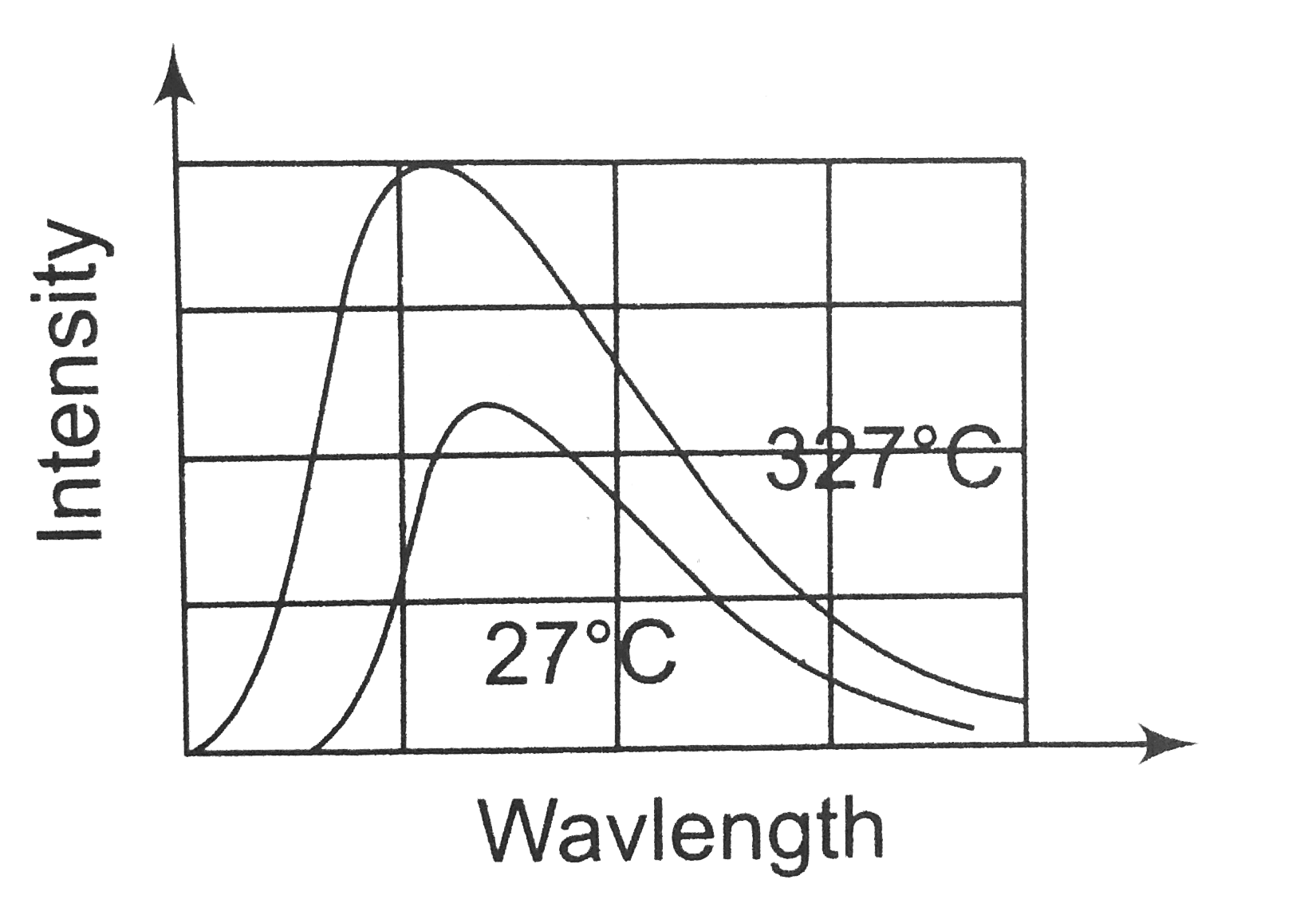 A16:1B8:1C9:4D16:9
A16:1B8:1C9:4D16:9
Let A0A1A2A3A4A5 be a regular hexagon inscribed in a circle of unit radius. Then the product of the lengths the line segments A0A1,A0A2 and A0A4 is
View SolutionTwo blocks are arranged as shown in figure. Find the ratio of a1/a2. (a1 is acceleration of m1 and a2 that of m2)
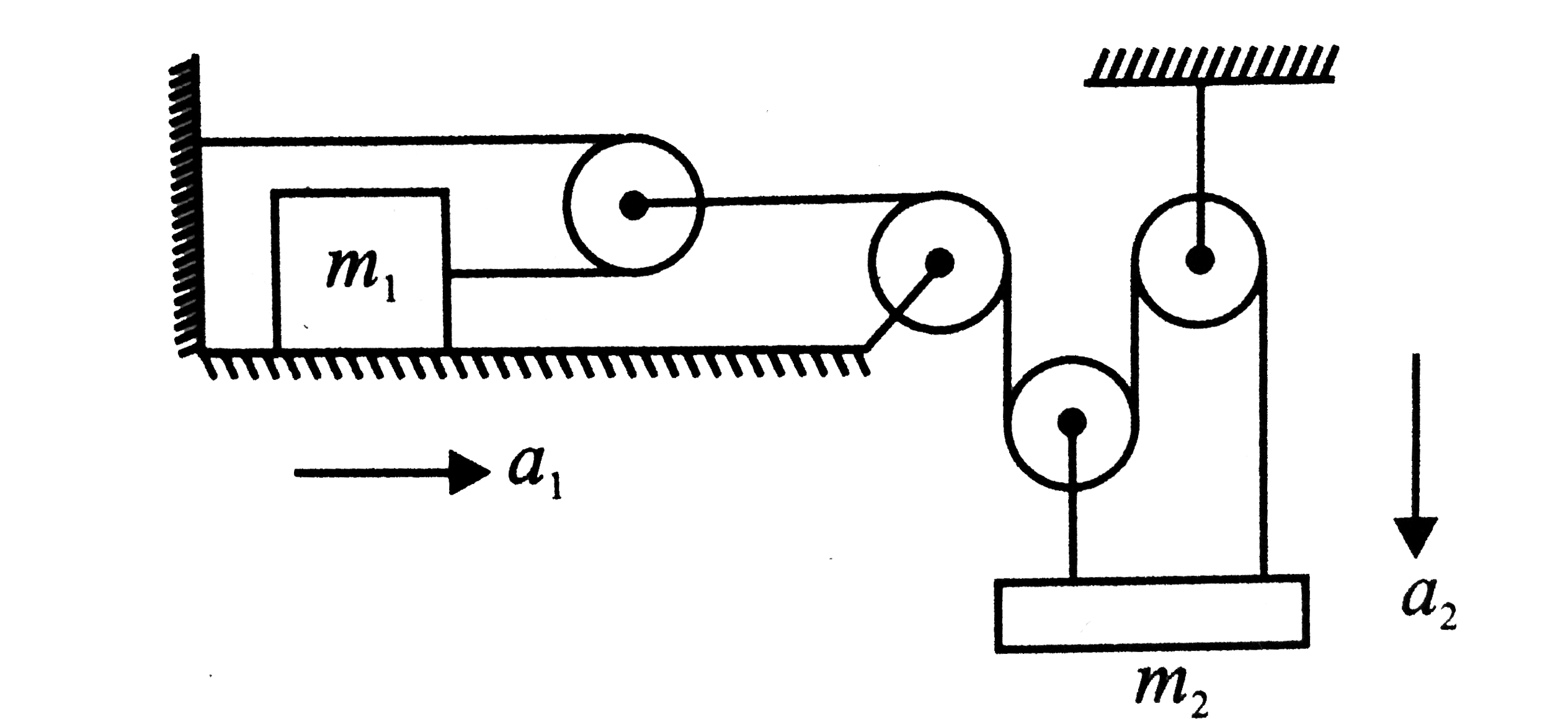 View Solution
View SolutionIn an acute angled triangle ABC,AA1 and AA2 are the medians and altitudes respectively. Length A1A2 is equal to
View SolutionLet A1A2A3……………….A14 be a regular polygon with 14 sides inscribed in a circle of radius 7 cm. Then the value of (A1A3)2+(A1A7)2+(A3A7)2 (in square cm) is……………..
View SolutionThe ratio of the areas of two triangles A1:A2 is 3:2. The corresponding bases are b1 and b2. The height of the triangles are equal. If b2=12cm. Find b1.
View Solution

