If the area of the circle is A1 and the area of the regular pentagon inscribed in the circle is A2, then find the ratio A1A2.
Step by step video & image solution for If the area of the circle is A_1 and the area of the regular pentagon inscribed in the circle is A_2, then find the ratio (A_1)/(A_2)dot by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
A regular pentagons is inscribed in a circle. If A1 and A2 represents the area of circle and that of regular pentagon respectively, then A1:A2 is
Aπ5cos(2π)5B2π5sin(2π)5C2π5 cosec 2π5D2π5cos(2π)5In the circuit of figure A1 and A2 are ideal ammeters. Then the reading in ammeter A2 is
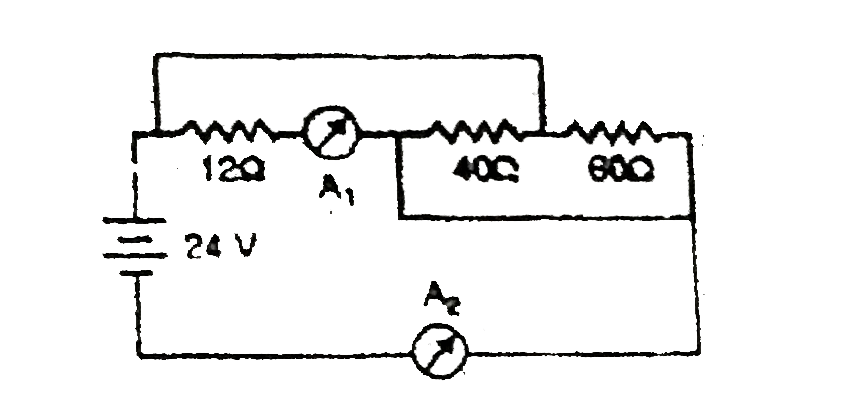 A0.4AB0.6AC2.0AD3.0A
A0.4AB0.6AC2.0AD3.0AThe capacitance of the capacitors of plate areas A1 and A2(A1<A2) at a distance d is
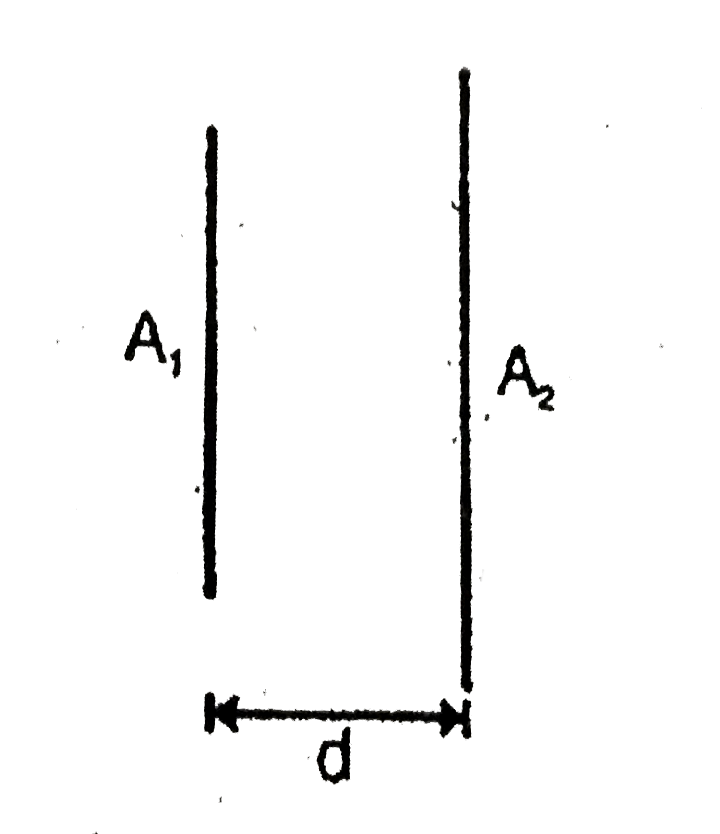 Aε0A1dBε0A2dCε0(A1+A2)2dDε0√A1A2d
Aε0A1dBε0A2dCε0(A1+A2)2dDε0√A1A2d
A circle is inscribed inside a regular pentagon and another circle is circumscribed about this pentagon.Similarly a circle is inscribed in a regular heptagon and another circumscribed about the heptagon. The area of the regions between the two circles in two cases are A1andA2, respectively. If each polygon has a side length of 2 units then which one of the following is true?
View SolutionIf the number of sides of two regular polygons having the same prerimeter be nand2n respectiely, prove that their areas are in the ratio 2cosπn:(1+cosπn)
View SolutionTwo parallel plate vacuum capacitors have areas A1 and A2 and equal plate spacing d. Show that when the capacitors are connected in parallel, the equivalent capacitance is the same as for a single capacitor with plate area A1+A2 and spacing d.
View SolutionTwo solid conductors are made up of same material have same length and same resistance . One of them has circular crosssection of area A1 and other one has square cross section of area A2. RATIO A1A2
View SolutionAtomic masses of two heavy atoms are A1 and A2. Ratio of their respective nuclear densities will be approximately
View Solution
