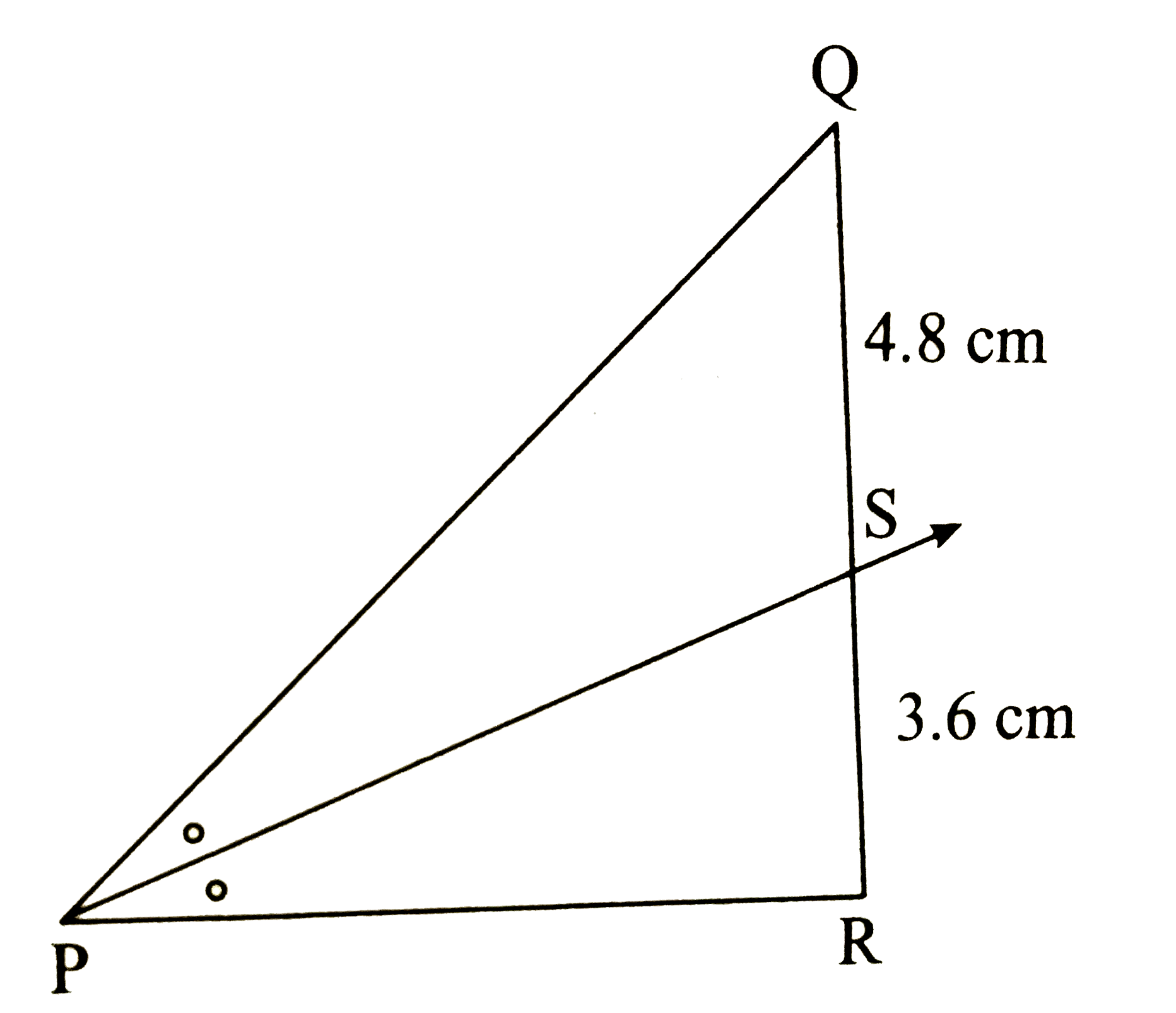
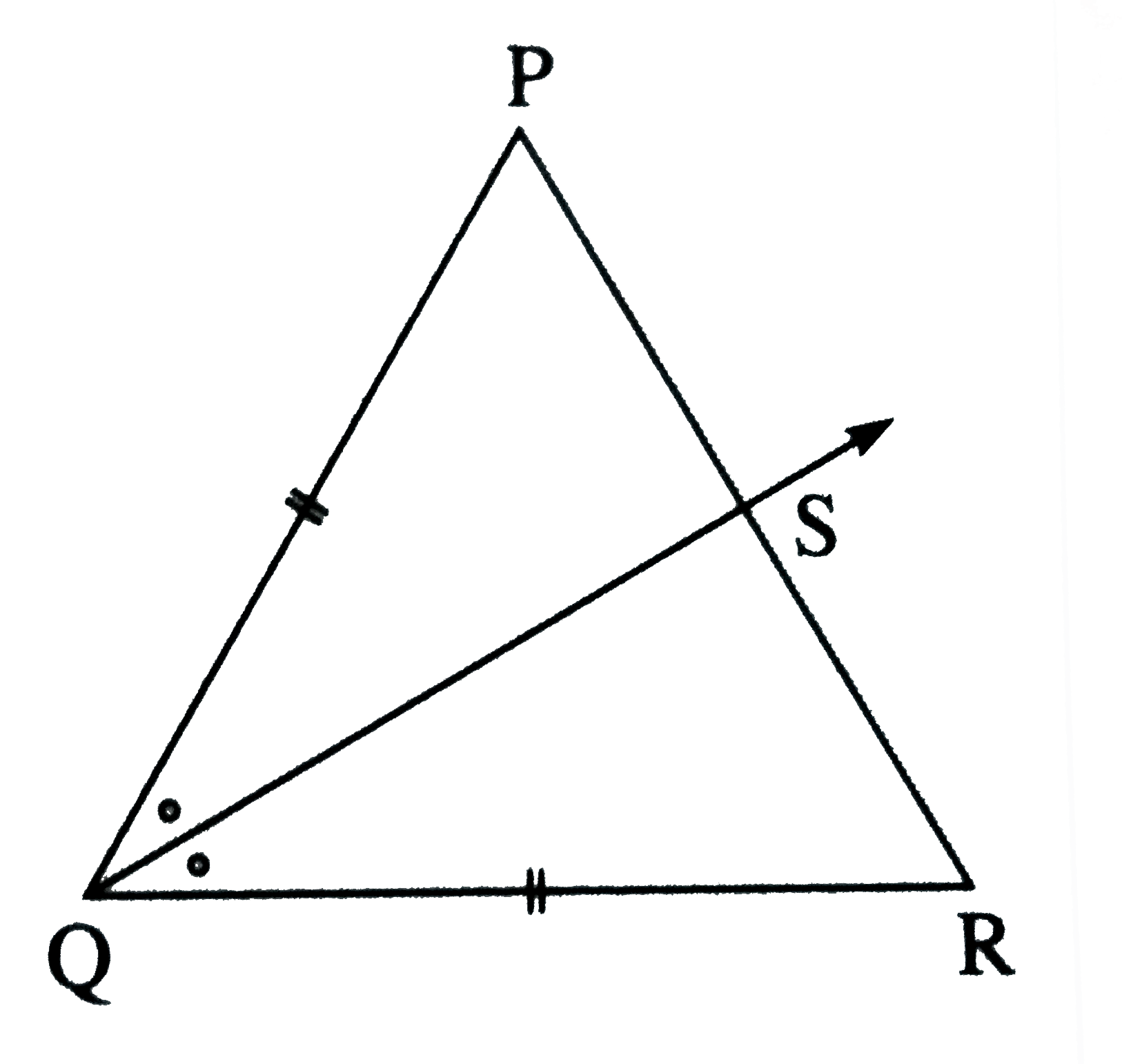
In ΔPQR, ray PS is the bisector of ∠QPR.
Q−S−R. If QS=4.8cm,SR=3.6cm then find PQ:PR.
The correct Answer is:PQ:PR=4:3
To solve the problem, we will use the Angle Bisector Theorem, which states that the ratio of the lengths of the two segments created by an angle bisector is equal to the ratio of the lengths of the other two sides of the triangle.
1. Identify the Given Information:
- In triangle PQR, ray PS is the bisector of angle QPR.
- Lengths given: QS=4.8cm and SR=3.6cm.
2. Apply the Angle Bisector Theorem:
- According to the Angle Bisector Theorem:
QSSR=PQPR
- Substituting the given values:
4.83.6=PQPR
3. Simplify the Ratio:
- To simplify 4.83.6, we can eliminate the decimals by multiplying both the numerator and the denominator by 10:
4836
- Now, simplify 4836 by dividing both the numerator and denominator by their greatest common divisor (GCD), which is 12:
48÷1236÷12=43
4. Express the Ratio:
- Therefore, we have:
PQPR=43
- This can be expressed as:
PQ:PR=4:3
5. Final Answer:
- The required ratio PQ:PR is 4:3.
- In triangle PQR, ray PS is the bisector of angle QPR.
- Lengths given: QS=4.8cm and SR=3.6cm.
- According to the Angle Bisector Theorem:
QSSR=PQPR
- Substituting the given values:
4.83.6=PQPR
- To simplify 4.83.6, we can eliminate the decimals by multiplying both the numerator and the denominator by 10:
4836
- Now, simplify 4836 by dividing both the numerator and denominator by their greatest common divisor (GCD), which is 12:
48÷1236÷12=43
- Therefore, we have:
PQPR=43
- This can be expressed as:
PQ:PR=4:3
- The required ratio PQ:PR is 4:3.
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - MCQ TYPE15videos
SIMILARITY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNEMENT 2.48videos
QUADRATIC EQUATIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - STATISTICSEXERCISE - EXAMPLES FOR PRACTICE (MCQs)35videos
STATISTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
In ΔPQR,∠Q>∠R PS is the bisector of ∠P and PT⊥PQ. If ∠SPT=28∘ and ∠R=23∘ then the measure of ∠Q is
A89∘B82∘C79∘D74∘
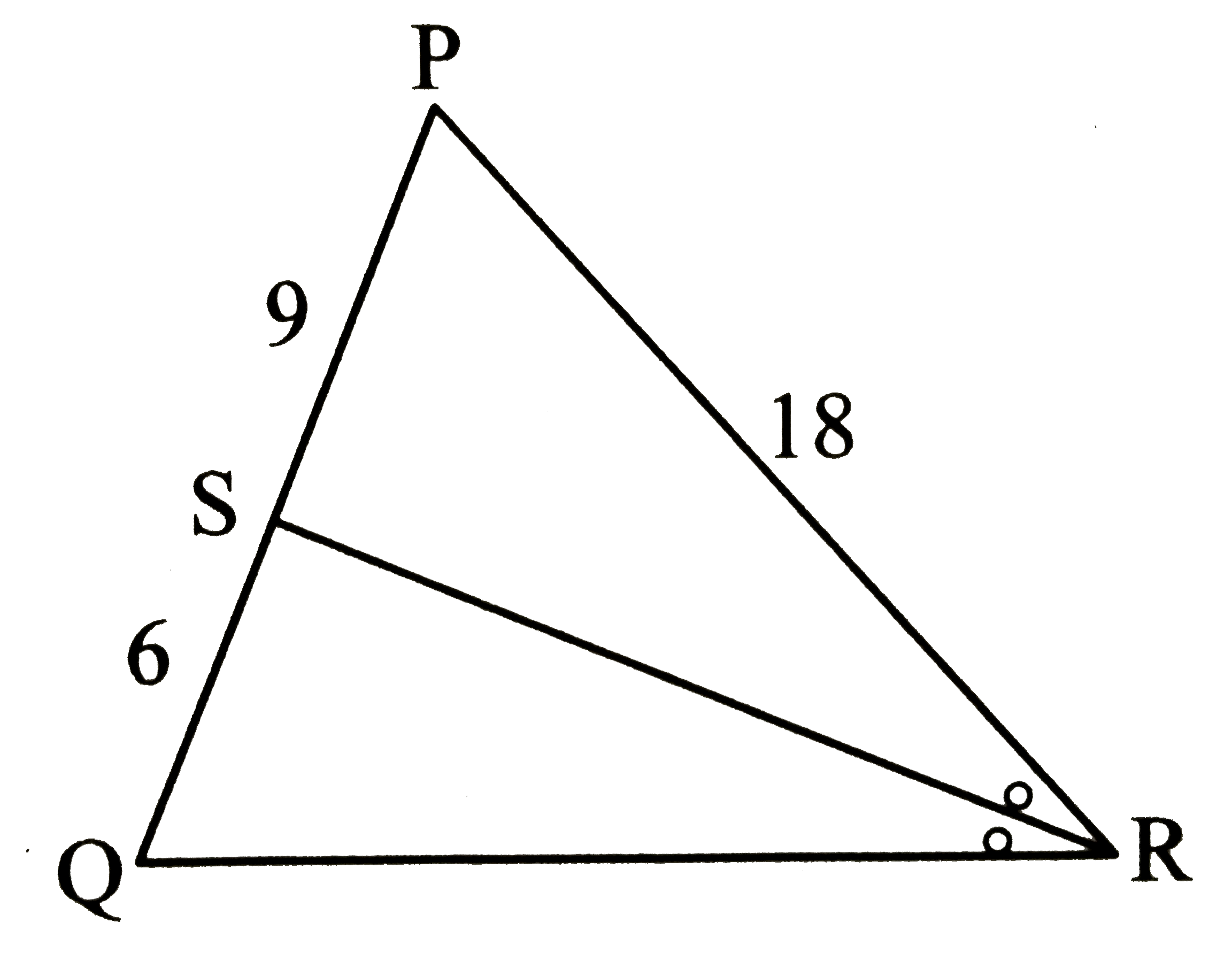
In the following figure, in ΔPQR,seg RS is the bisector of ∠PRQ,PS= 6, SQ=8, PR = 15, Find QR.
 View Solution
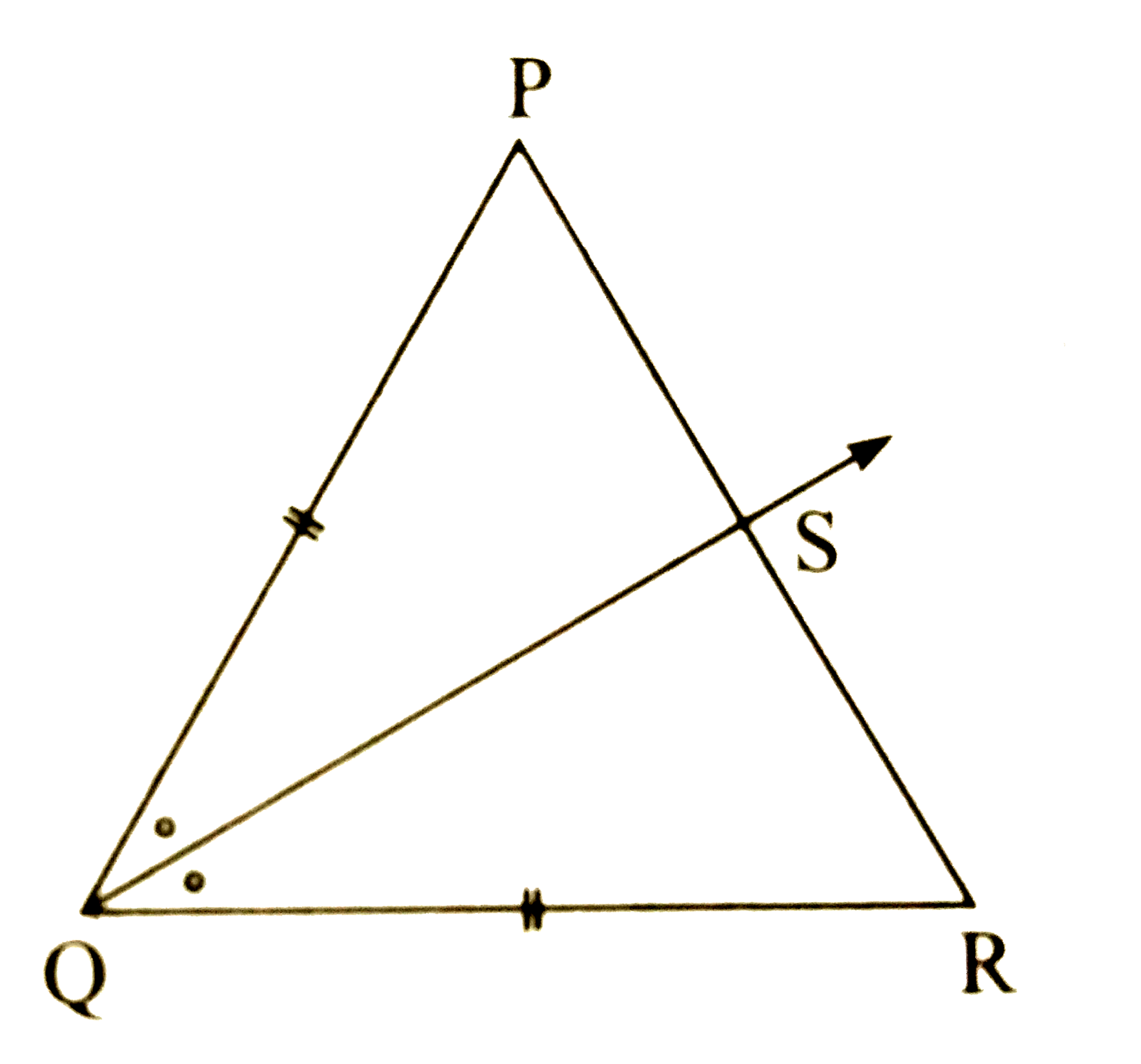
View SolutionIn the figure, ray QS is the bisector of ∠PQR and PQ=QR.
Then PSSR=………..
 View Solution
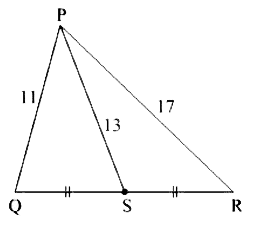
View SolutionIn ΔPQR, point S is the midoint of side QR. If PQ=11,PR=17,PS=13, Find QR.
 View Solution
View SolutionIn the figure ray QS is the bisector of ∠PQR and PQ=QR, then PSSR=………..
 View Solution
View SolutionIn △PQR, PS is the internal bisector of ∠P meeting QR at S, PQ =16cm, PR = 22.4 cm and QR = 9.6cm. The length of SR(in cm) is:
△PQR में, PS, ∠P , का आंतरिक द्विभाजक है जो QR से S पर मिलता है l यदि PQ = 16cm, PR = 22.4 cm और QR = 9.6 cm तो SR (सेमी में) की लंबाई हैView SolutionIn ΔPQR, point S is the midpoint of side QR. If PQ =11, PR =17 PS =13 , find QR.
View SolutionIn the following figure, in ΔPQR, seg RS is the bisector of ∠PQR,PS=6,SQ=8,PR=15.
Find QR.
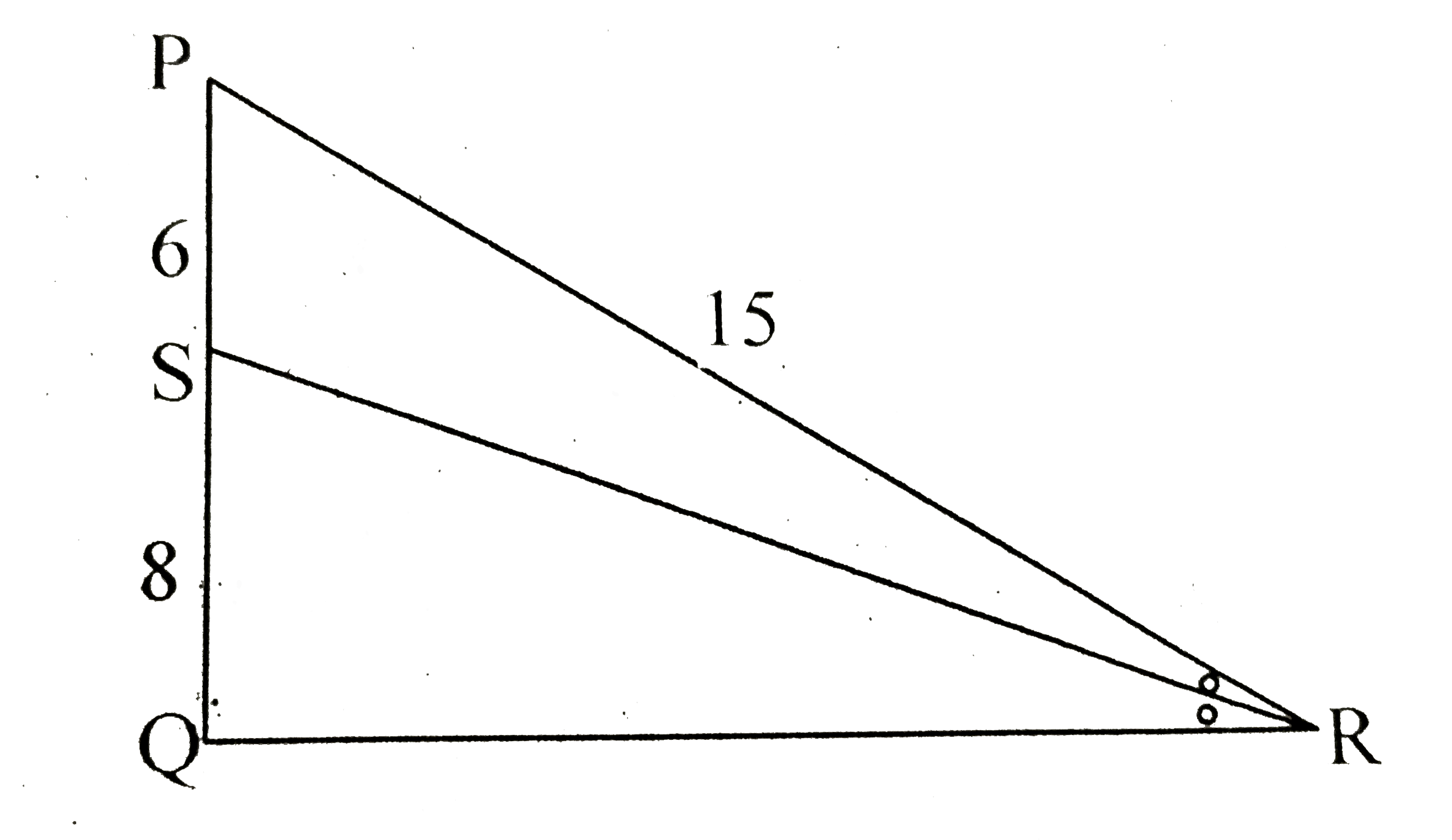 View Solution
View Solution