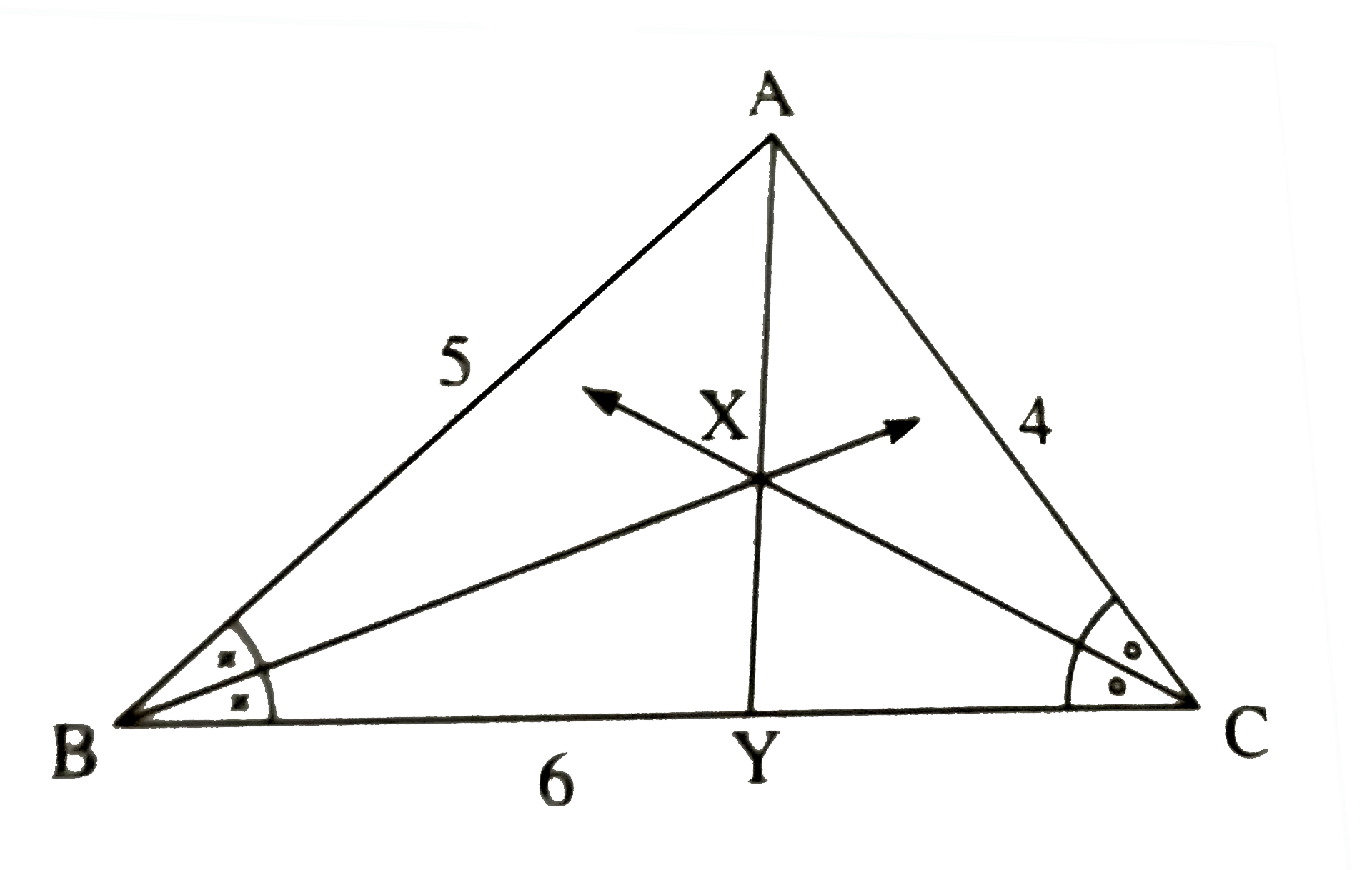
Bisector of ∠B and ∠C in ΔABC meet each other at P. Line AP cuts the sides BC at Q.
Prove: APPQ=AB+ACBC.
NA
Topper's Solved these Questions
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - MCQ TYPE
15 Videos
- QUADRATIC EQUATIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNEMENT 2.4
8 Videos
- STATISTICSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - STATISTICSEXERCISE - EXAMPLES FOR PRACTICE (MCQs)
35 Videos
Similar Questions
Knowledge Check
The mid points of AB and AC of the ΔABC are P and Q respectively. If PQ=6cm, then the side BC is
A10 cm.B12 cm.C8 cm.D14 cm.
ΔABC is an isosceles, with AB=AC. If P be any point on the side BC. Prove that AP<AB.
View SolutionA line cuts two sides AB and AC of ΔABC at points P and Q respectively. Prove A(ΔAPQ)A(ΔABC)=AP×AQAB×AC.
View SolutionInternal bisector of ∠A of triangle ABC meets side BC at D. A line drawn through D perpendicular to AD intersects the side AC at E and the side AB at F. If a, b, c represent sides of ΔABC, then
View SolutionIn △ ABC, the bisectors of ∠B and ∠ C intersect at I. A line drawn through I and parallel to BC intersects AB at P and AC at Q. Prove that PQ = BP + CQ.
View SolutionΔABC is a right triangle right angled at A such that AB=AC and bisector of ∠C intersects the side AB at D. Prove that AC+AD=BC.
View SolutionIn the given figure ,P is a point on the side BC of △ABC.Prove tat (AB+BC+AC)GT2AP
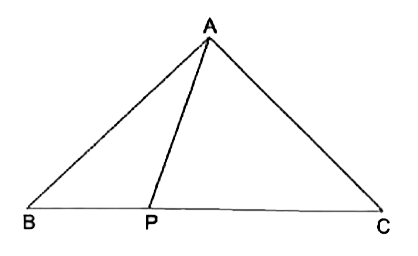
View SolutionThe side BC of ΔABC is product to N. bisector of angle meets BC at M. Prove that ∠ABC+∠ACN=2∠AMC
View Solution