The tangent drawn at points P and Q on the circumference of a circle intersect at A. If ∠PAQ=60∘, find the value of ∠APQ. Solution in Bengali
Let P and Q be any two points on the circle with centre O. Two tangents AP and AQ drawn at the points P and Q intersect each other at the point A. Let us join P, Q and O, A
Given that ∠PAQ=60∘.
Now, Ap is a tangent to the circle with centre O and OP is the radius passing through the point of contact P.∴OP⊥AP,∴∠OPA=90∘.
Similarly, ∠OQA=90∘
In Δ'sPOAandΔQOA,
∠OPA=∠OQA[∵ each is a right-angle]
OP=OQ[∵ radius of same circle] and hypotenuse OA is common to both
∴ΔPOA≡ΔQOA [by the R-H-S condition of congruency ]
therefero∠OAP=∠OAQ [similar angles of congurent triangles ]
Given that ∠PAQ=60∘or,∠PAO+∠QAO=60∘
or, ∠PAO=60∘∠QAO=∠PAO]
or, 2∠PAO=60∘or,∠PAO=60∘2=30∘
Then, ∠PAO90∘−∠OAP=90∘−30∘=60∘[∵∠OAP=∠PAO=30∘]
∴∠APQ=∠APO−∠OPQ=90∘−30∘=60∘
∴ value of ∠APQ=60∘.

Topper's Solved these Questions
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.120videos
THEOREMS RELATED TO TANGENT IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.223videos
THEOREMS RELATED TO TANGENT IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.3 (Long Answer Type Questions)14videos
THEOREMS RELATED TO ANGLES IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES EXERCISE - EXERCISE66videos
TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES
Similar Questions
PR and PS are two tangents drawn from a extental point P of the Circle with centre at O. If PR=8cmand∠RPO=60∘, then the length of PS=
05:08View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
02:46View SolutionProve that angle in the segment of a circle which is greater than a semi-circle is an acute angle.
01:54View SolutionIf tanθ=pq, what is the value of psecθ−q cosecθpsecθ+q cosecθ=
03:15View SolutionA pair of tangents are drawn to a unit circle with centre at the origin and these tangents intersect at point P enclosing an angle of 60^(@) . The area enclosed by the tangents and the arc of the circle is,
02:27View SolutionP केंद्र वाले, वृत्त के व्यास AB के अंतिम बिन्दुओ पर दो स्पर्श रेखाएं खींची गई। यदि बिंदु C से वृत्त पर खींची गई स्पर्श रेखा, अन्य दो स्पर्श रेखाओ को Q तथा R पर प्रतिछेदित करती है। ∠QPR का मान ज्ञात करे?
03:41View Solutionमाना कि केंद्र बिन्दु O वाले वृत्त पर P और Q दो बिन्दू है । यदि वृत्त के दो बिन्दू P और Q से होकर खींची गई स्पर्श रेखाएं A पर मिलती है, तो ∠PAQ=48∘,then ∠APQ कितना होगा ?
05:17View Solutionदो सर्वांगसम वृत्त परस्पर बिंदुओं A और B पर प्रतिच्छेद करते है । A से होकर कोई रेखाखंड PAQ इस प्रकार खींचा गया है कि P और Q दोनों वृत्तों पर स्थित है । सिद्ध कीजिए कि BP=BQ है ।
09:02View Solutionदिये गए चित्र में O केन्द्र वाले एक वृत्त के बिन्दु A पर PAQ एक स्पर्शी है तथा ∠BAQ=60∘ तब ∠ABC का मान ज्ञात कीजिए ।
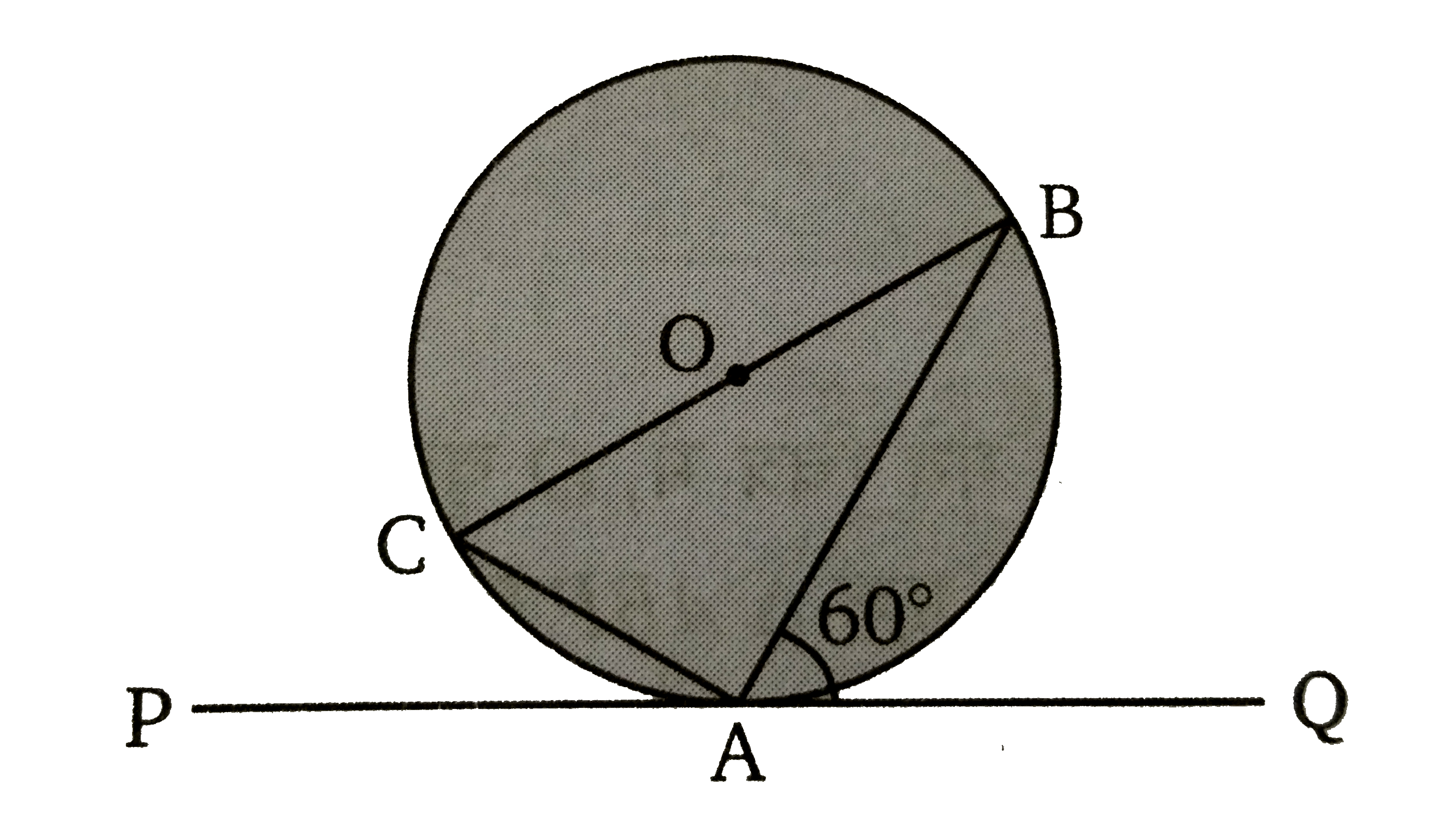 03:53View Solution
03:53View Solutionदिये गए चित्र में, O वृत्त का केन्द्र है तथा वृत्त के बिन्दु P पर T'PT एक स्पर्शी है। इसके अन्दर एक △ABP खींचा गया है। यदि ∠BPT=60∘ तब ∠BAP का मान ज्ञात कीजिए ।
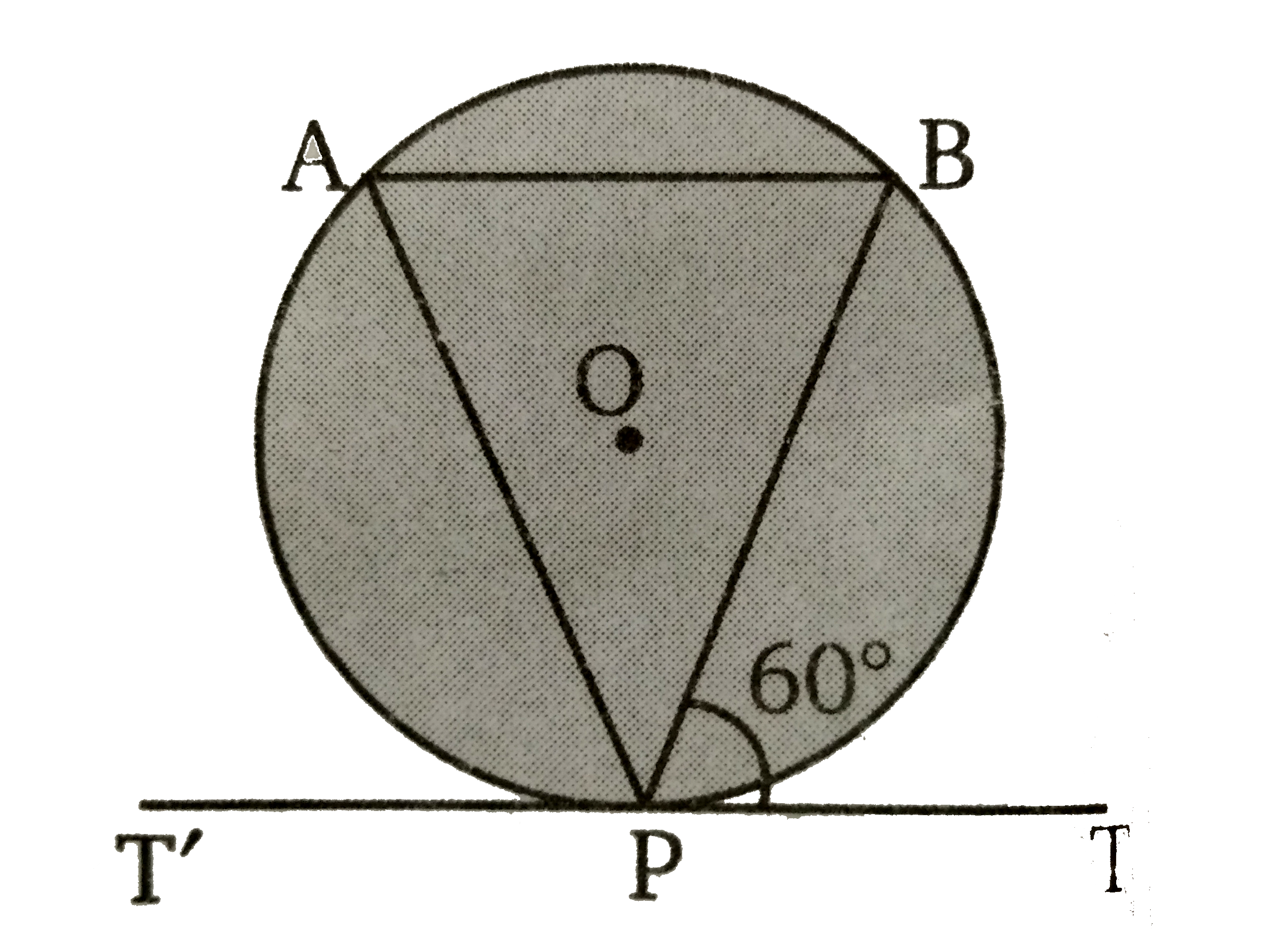 02:06View Solution
02:06View SolutionXY is a diameter of a circle. PAQ is a tangent to the circle at the point A lying on the circumference. The perpendicular drawn on the tangent to the circle from X intersects PAQ at Z. Prove that XA is a bisector of ∠YXZ. [GP−X]
02:44View SolutionTwo chords AC and BD of a circle intersect each other at the point O. If two tangents drawn at the points A and B intersect each other at the point P and two tangents drawn at the points C and D intersect at the point Q, prove that ∠P+∠Q=2∠BOC.[GP−X]
02:17View SolutionIn the figure, O is the centre and BOA is a diameter of the circle. A tangent drawn to the circels at the point P intersects the extended BA at the point T. If ∠PBO=30∘, find the value of ∠PAT.
03:16View SolutionTwo tangents drawn at the point A and B on a circle intersect each other at the point P. If ∠APB=60∘, then ∠PAB=
02:44View Solutionयदि O केन्द्र और a त्रिज्या के वृत्त पर बाह्य बिन्दु P से खींची गई दो स्पर्श रेखाओं के मध्य कोण 60∘ है, तो OP की लम्बाई ज्ञात कीजिए।
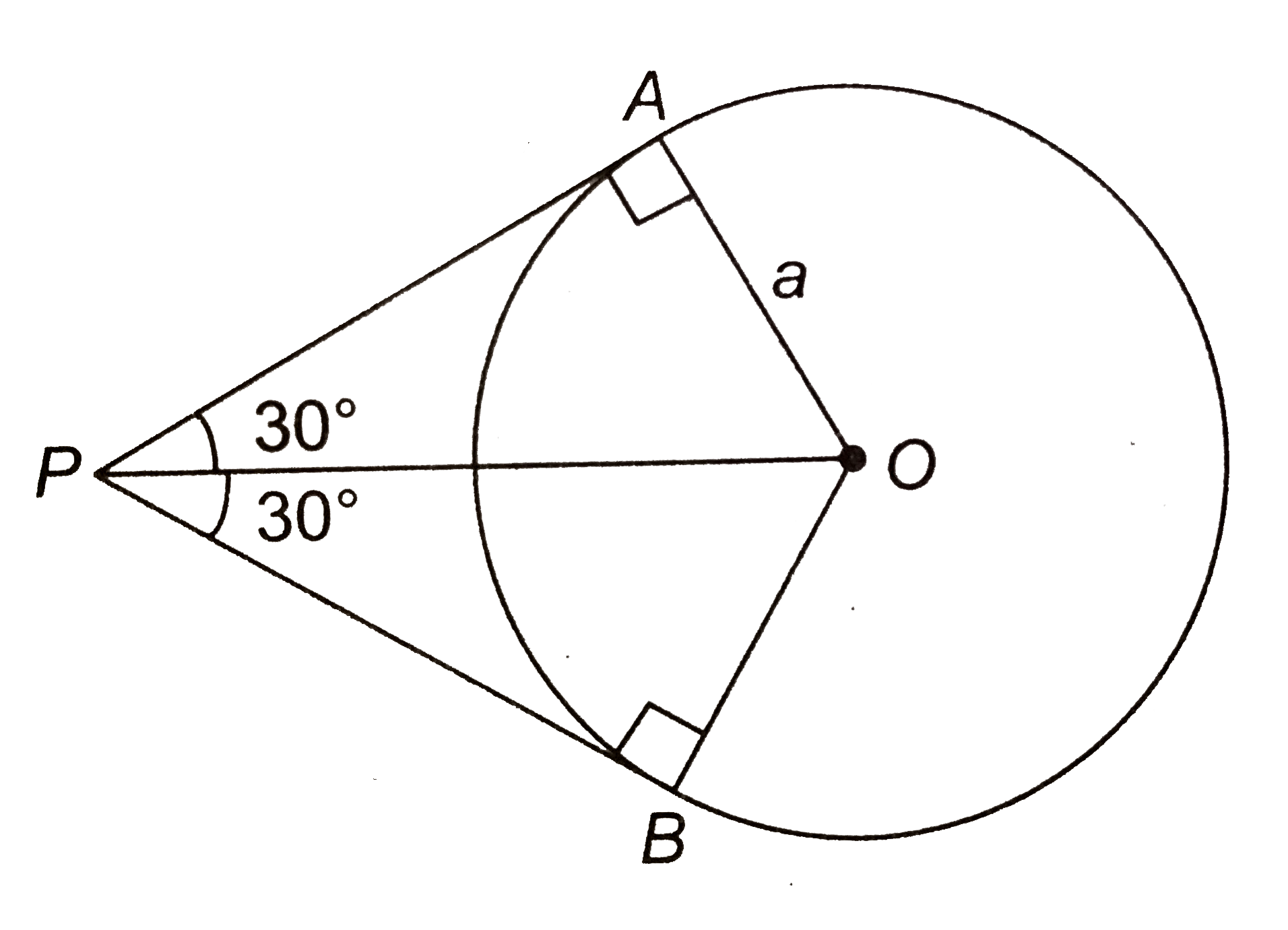 09:10View Solution
09:10View SolutionTwo tangent are drawn from external point P to circle of radius 3 , such that angle between them is 60^@ , then length of tangents is
02:44View Solution

