If the medians of a △ABC intersect at G, show that
ar(△AGB)=ar(△AGC)=ar(△BGC)
=13ar(△ABC).
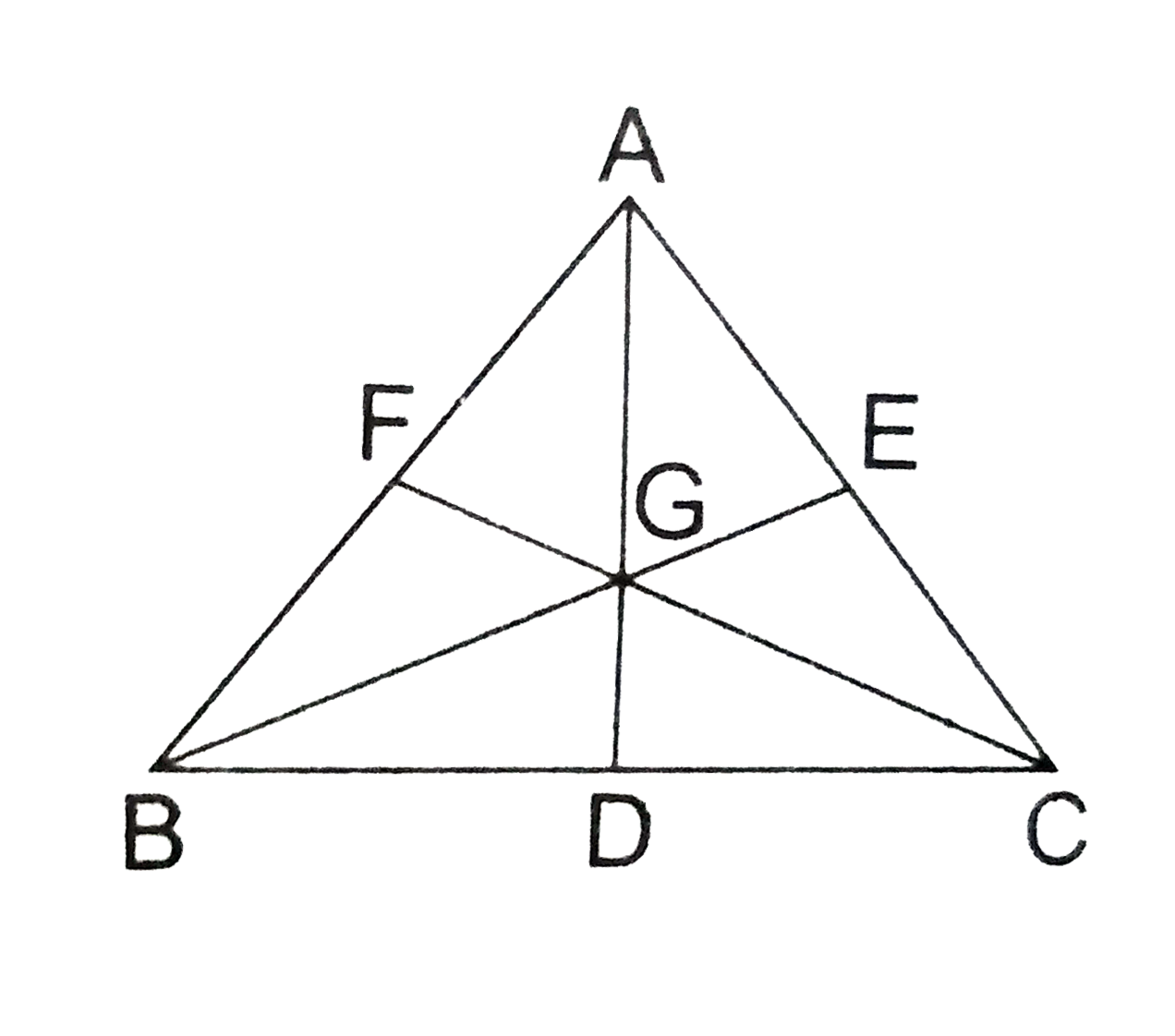
GIVEN:
A △ABC. Its medians AD,BE and CF intersect at G.
TO PROVE ar(△AGB)=ar(△AGC)=ar(△BGC)=13ar(△ABC)
PROOF:
We know that a median of a triangle divides it into two triangle of equal area.
In △ABC ,AD is the median.
∴ar(△ABD)=ar(△ACD). ...(i)
In △GBC, GD is the median.
∴ar(△GBD)=ar(△GCD). ...(ii)
From (i) and (ii), we get
ar(△ABD)−ar(△GBD)=ar(△ACD)−ar(△GCD)
⇒ar(△AGB)=ar(△AGC).
Similarly, ar(△AGB)=ar(△BGC).
⇒ar(△AGB)=ar(△AGC).
But, ar(△ABC)=ar(△AGB)+ar(△AGC)+ar(△BGC)
=3ar(△AGB) [using (iii)].
∴ar(△AGB)=13ar(△ABC).
Hence, ar(△AGB)=ar(△AGC)=ar(△BGC)=13ar(△ABC).
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - Exercise 1138videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)32videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)16videos
AREAS OF TRIANGLES AND QUADRILATERALS
Similar Questions
In the adjoining figure, ABC and BDE are two equilateral triangle such that D is the midpoint of BC. If AE intersects BC at F, show that
(i)ar(△BDE)=14ar(△ABC)
(ii)ar(△BDE)=12ar(△BAE)
(iii)ar(△ABC)=2ar(△BEC)
(iv)ar(△BFE)=ar(△AFD)
(v)ar(△BFE)=2ar(△FED)
(vi)ar(△FED)=18ar(△AFC).
 View Solution
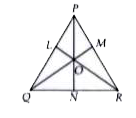
View SolutionIf the medians of ΔPQR intersect at O, then ar (ΔPOQ) =
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
If ABCD is a tetrahedron such that each △ABC,△ABDand△ACD has a right angle at A. If ar(△(ABC))=k1,ar(△ABD)=k2,ar(△BCD)=k3, then ar(triangleACD) is
A√k21+k22+k23B√k1k2k3k21+k22+k23C√∣∣(k21+k22−k23)∣∣D√∣∣(k21−k22−k23)∣∣ - Question 2 - Select One
ABCD is a tetrahedron such that each of the △ABC, △ABD and △ACD has a right angle at A. If ar(△ABC)=k1.ar(△ABD)=k2,ar(△BCD)=k3, then ar(△ACD) is
A√k21+k22+k23B√k1k2k3k1+k2+k3C√∣∣k21+k22−k23∣∣D√∣∣k22−k21−k23∣∣ - Question 3 - Select One
In △ABC, P is the mid-point of BC and Q is the mid-point of AP. Find the ratio of the area of △ABQ and the area of ∠ABC. The following are the steps involved in solving the above problem.
A) We know that a a median of a triangle divides a triangle into two triangles of equal area.
B) ⇒Ar(△ABP)=12[Ar(△ABC)]
C) Ar(△ABQ)=12[Ar(△ABP)]=14[Ar(△ABC)]
D) ⇒(△ABQ):Ar(△ABC)=1:4AABCDBADBCCABCDDADCB
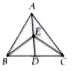
In the figure, E is any point on median AD of a △ABC. Show that ar(△ABE)= ar(△ACE).
 View Solution
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar(△BED)=14ar(△ABC).
View SolutionIn the figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar(△APB)+ar(△PCD=12ar(ABCD)
(ii) ar(△APD)+ar(△PBC)=ar(△APB)+ar(△PCD)
 View Solution
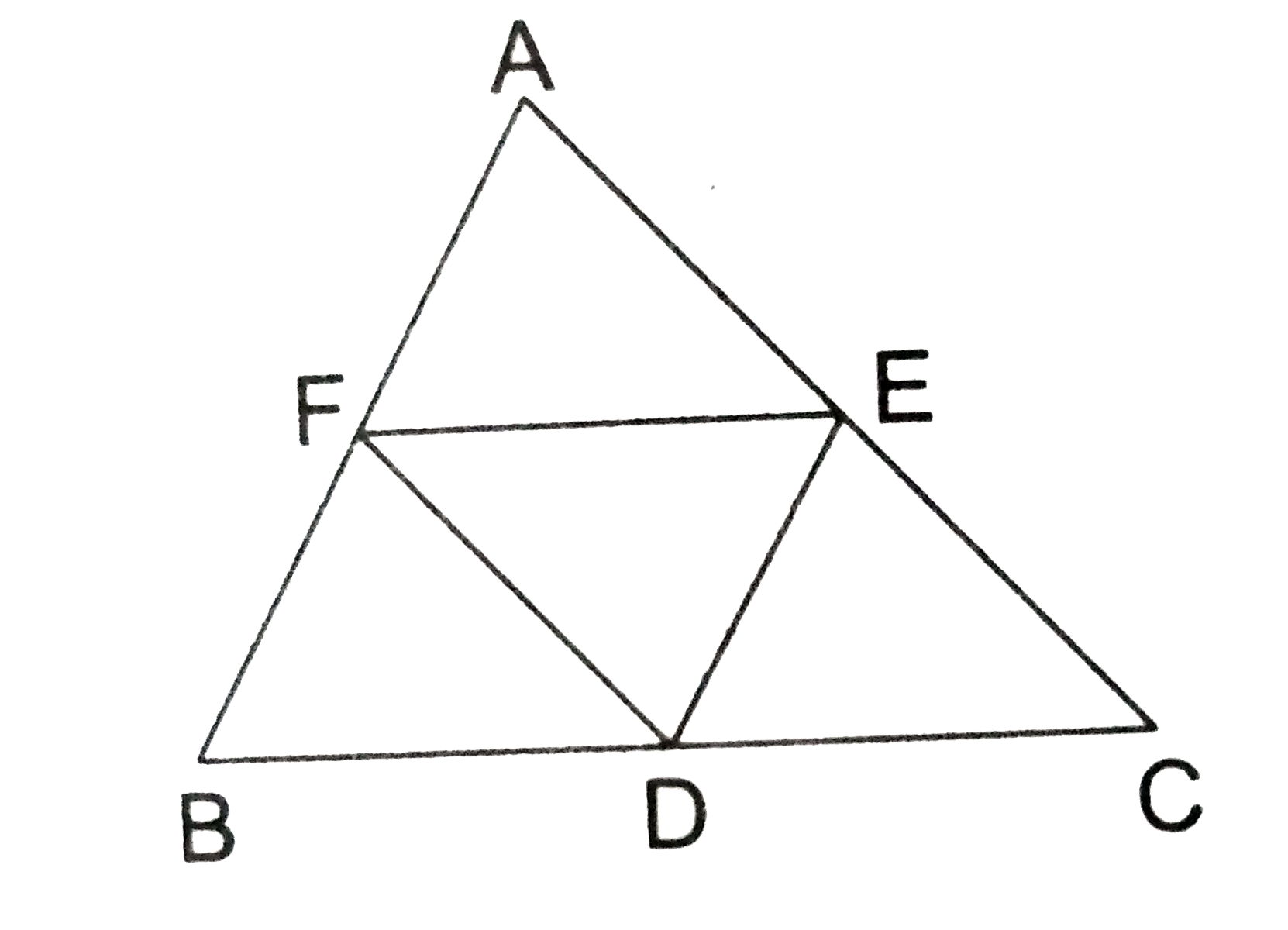
View SolutionD, E, F are the midpoints of the sides BC, CA and AB respectively of △ABC. Prove that
(i) BDEF is a ||gm,
(ii) ar(△DEF)=14ar(△ABC)and
(iii) ar(||gm BDEF)=12ar(△ABC)
 View Solution
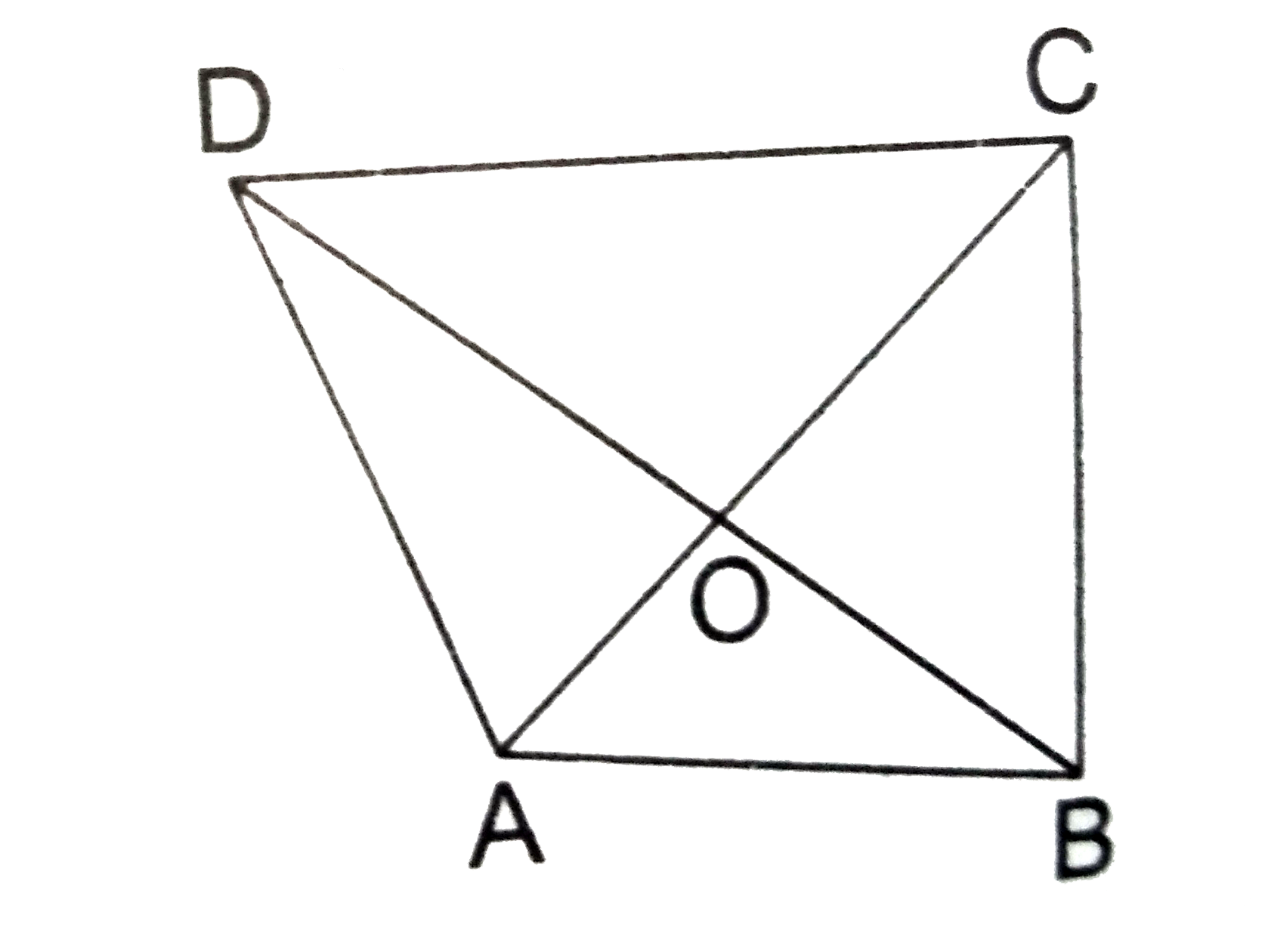
View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O.
If BO=OD, prove that
ar(△ABC)=ar(△ADC).
 View Solution
View Solution
