Using the method of integration, show that the volume of a right circular cone of base radius r and height h is V=13πr2h.
Video Solution
Text Solution
Let ABC be the right circular cone. Consider a circular secition of the cone DE, with plane parallel to its base, of thickness dx, at a distance of x from the apex A.
If y be its radius, then from similar triangles, AOC and AO′E, we have
yx=rh⇒y=rxh
Therefore, area of the circular section DE=πy2=πr2x2h2
Therefore, volume of the circular section DE=πr2x2dxh2
i.e., dV=πr2x2dxh2
Now, the total volume of the cone can be obtained as the summation (integration) of the volumes of each circular sections such as DE, i.e.,
V=∑dV=h∫0πr2x2dxh2=πr2h2[x33]h0
=πr23h2[h3−0]=πr2h3

|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.12videos
BASIC MATHEMATICS
- BOOK - CENGAGE PHYSICSCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.23videos
BASIC MATHEMATICS
- BOOK - CENGAGE PHYSICSCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.620videos
BASIC MATHEMATICS
- BOOK - CENGAGE PHYSICSCHAPTER - ARCHIVES 2 VOLUME 6EXERCISE - Integer4videos
ARCHIVES 2 VOLUME 6
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
The volume of a right circular cone of height 12cm and base radius 6cm, is
A(12π)cm3B(36π)cm3C(72π)cm3D(144π)cm3 - Question 2 - Select One
The ratio of the volume of a right circular cylinder and a right circular cone of the same base and height will be :
A2:3B1:3C3:1D9:1
Determine the coordinates of the centre of mass of a right circular soild cone of base radius R and height h.
View SolutionDetermine the coordinate of the centre of mass of a right circular solid cone of base radius R and height h.
View SolutionFind the total surface area of a wooden right circular cylinder of base radius 'r' and height 'h'
View SolutionThe curved surface area of a cone of base radius r and height h is_______.
View SolutionShow that the volume of a segment of height h of a sphere of radius R is
V=13πh2(3R−h)
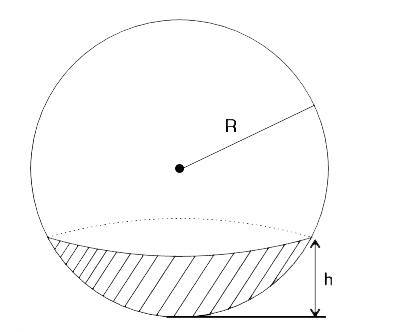 View Solution
View SolutionCurved surface area of a right circular cylinder is 4.4m2. If the radius of the base of the cylinder is 0.7 m, find its height.
View Solution

