Show that the volume of a segment of height h of a sphere of radius R is
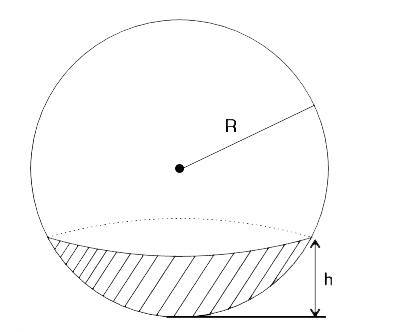
Step by step video & image solution for Show that the volume of a segment of height h of a sphere of radius R is V=(1)/(3)pi h^(2)(3R-h) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
If h is the height, I the slant height and r1,r2 radii of the circular bases of the frustum of a cone, then slant height of the frustum = √(r1−r2)2+h2. Height of the cone of which the frustum is a part = (hr1/(r1−r2).We have a bucket in the form of frustum of a cone in which h = 8 cm, r1 = 9 cm and r2 = 3 cm. Find its volume.
A321πcm3B312πcm3C108πcm3D324πcm3
Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is 2R√3. Also find the maximum volume.
View SolutionShow that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is 2R√3 . Also find maximum volume.
View SolutionTwo soap bubbles are stuck together with an intermediate film separating them. Compute the radius of curvature of this film given that the radii of the bubbles in this arrangement are r1 and r2 respectively. If r1>r2 state clearly which way the intermediate film will bulge.
For the case when r1=r2=2cm calculate he radius of the bubble formed by bursting the intermediate film. The volume of a spherical dome of radius R and height h is πb2(3R−b)/3.
View SolutionShow that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is 2R√3 .
View SolutionShow that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius R is 4R3.
View SolutionFrame the formula for the volume (v) of a cylinder given by the product of π, square of radius (r) and height (h).
View SolutionFrame the formula for the volume (v) of a cylinder given by the product of π, square of radius (r) and height (h).
View Solution