A cube is placed so that one corner is at the origin and three edges are along the x-,y-, and ,z-axes of a coordinate system (figure).Use vector to compute
a.The angle between the edge along the z-axis (line ab) and the diagonal from the origin to the opposite corner (line ad).
b. The angle between line ac (the diagonal of a face ) and line ad.

Video Solution

Text Solution

Verified by Experts

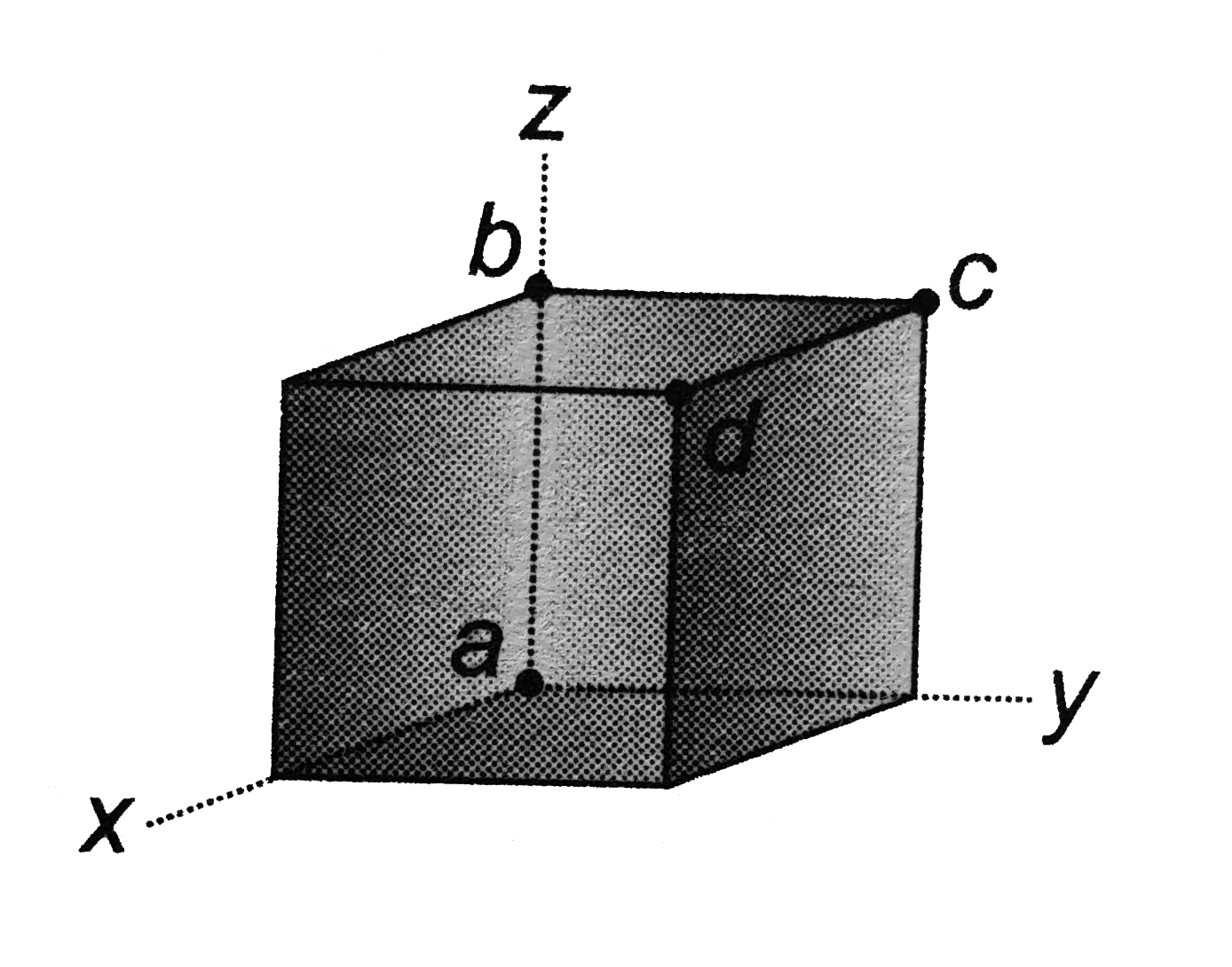
The correct Answer is:a. $\cos^{- 1} (\frac{1}{\sqrt{3}})$ ; b. cos^(-1)(sqrt(2)/sqrt(3))

a.Let side of the cube is $d$ ,then $\vec{a b} = d \hat{k}$ and $\vec{a d} = d \hat{i} + d \hat{j} + d \hat{k}$
$\cos θ = \frac{\vec{a b} . \vec{a d}}{| \vec{a b} | | \vec{a d} |} = \frac{d^{2}}{d \sqrt{3 d}} = \frac{1}{\sqrt{3}} \Rightarrow θ = \cos^{- 1} (\frac{1}{\sqrt{3}})$
$\vec{a c} = d \hat{j} + d \hat{k}$
$\cos θ = \frac{\vec{a c} . \vec{a d}}{| \vec{a c} | | \vec{a d} |} = \frac{2 d^{2}}{\sqrt{2 d \sqrt{3 d}}} = \frac{\sqrt{2}}{\sqrt{3}}$
$\Rightarrow \cos^{- 1} (\frac{\sqrt{2}}{\sqrt{2}})$

|

Updated on:21/07/2023

Class 11 PHYSICS VECTOR

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The direction rations of the diagonals of a cube which joins the origin to the opposite corner are (when the three concurrent edges of the cube are coordinate axes)
A $(\frac{2}{\sqrt{2}}, \frac{2}{\sqrt{3}}, \frac{2}{\sqrt{3}})$
B(1,1,1)
C(2,-2,1)
D(1,2,3)
Question 2 - Select One
Three thin uniform rods each of mass M and length L and placed along the three axis of a Cartesian coordinate system with one end of each rod at the origin. The M.I. of the system about z-axis is
A $\frac{M L^{2}}{3}$
B $\frac{2 M L^{2}}{3}$
C $\frac{2 M L^{2}}{6}$
D $M L^{2}$
Question 3 - Select One
Comprehesion-I
Let k be the length of any edge of a regular tetrahedron (all edges are equal in length). The angle between a line and a plane is equal to the complement of the angle between the line and the normal to the plane whereas the angle between two plane is equal to the angle between the normals. Let O be the origin and A,B and C vertices with position vectors $\to a, \to b$ and $\to c$ respectively of the regular tetrahedron.
The angle between any edge and a face not containing the edge is
A ${cos}^{- 1} (\frac{1}{2})$
B ${cos}^{- 1} (\frac{1}{4})$
C ${cos}^{- 1} (\frac{1}{\sqrt{3}}$
D ${cos}^{- 1} (\frac{\sqrt{3}}{2})$

CENGAGE PHYSICS-VECTORS-Exercise Subjective

Home
Ask Doubt
Profile