A cube of side l has one corner at the origin of coordinates and extends along the positive x−,y−andz−axes. Suppose that the electric field in this region is given by →E=(a+by)ˆj. Determine the charge inside the cube (a and b are some constants).
The faces adhe, bcgf, cdhg, and abfe will contribute zero flux because the area vector is normal to the electric field for these faces.

Flux through face efgh is
ϕ1=∫→E⋅d→A=a(ˆj)⋅l2(−ˆj)=−at2
The field at the face efgh (that lies in the yz- plane , y = 0) is →E=aˆj
and the area vector is l2(−ˆj) (direction outward normal). Flux through face abcd is
ϕ2=(a+bl)ˆj⋅l2ˆj=(al2+bl3) (for this y = l)
Net flux through the cube is ϕ1+ϕ2=bl3. From Gauss's law,
ϕ=Qenclosedε0orQenclosed=ε0ϕE=ε0bl3.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Example7videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Exercise 2.116videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger8videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.514videos
ELECTRIC POTENTIAL
Similar Questions
A cube has sides of length L=0.2 m It is placed with one corner at the origin as shown in figure The electric field in uniform and given by →E=(2.5ˆi−4.2ˆj)N/C .Find the electric flux through the entire cube.
 View Solution
View SolutionA cube is placed so that one corner is at the origin and three edges are along the x-,y-, and ,z-axes of a coordinate system (figure).Use vector to compute
a.The angle between the edge along the z-axis (line ab) and the diagonal from the origin to the opposite corner (line ad).
b. The angle between line ac (the diagonal of a face ) and line ad.
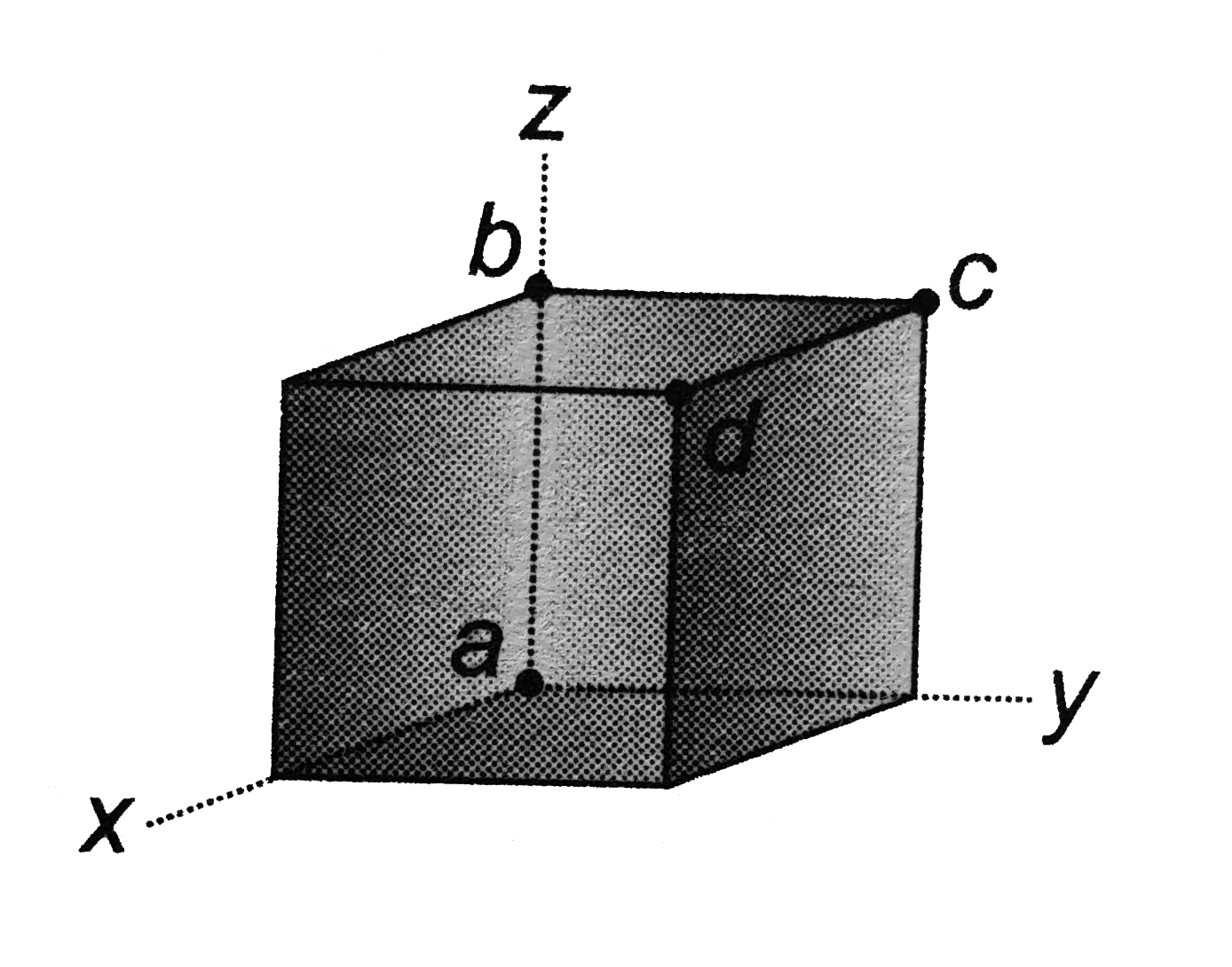 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Due to a charge inside the cube, the electric field is: Ex = 600x, Ey = 0, Ez = 0. The charge inside the cube is nearly -
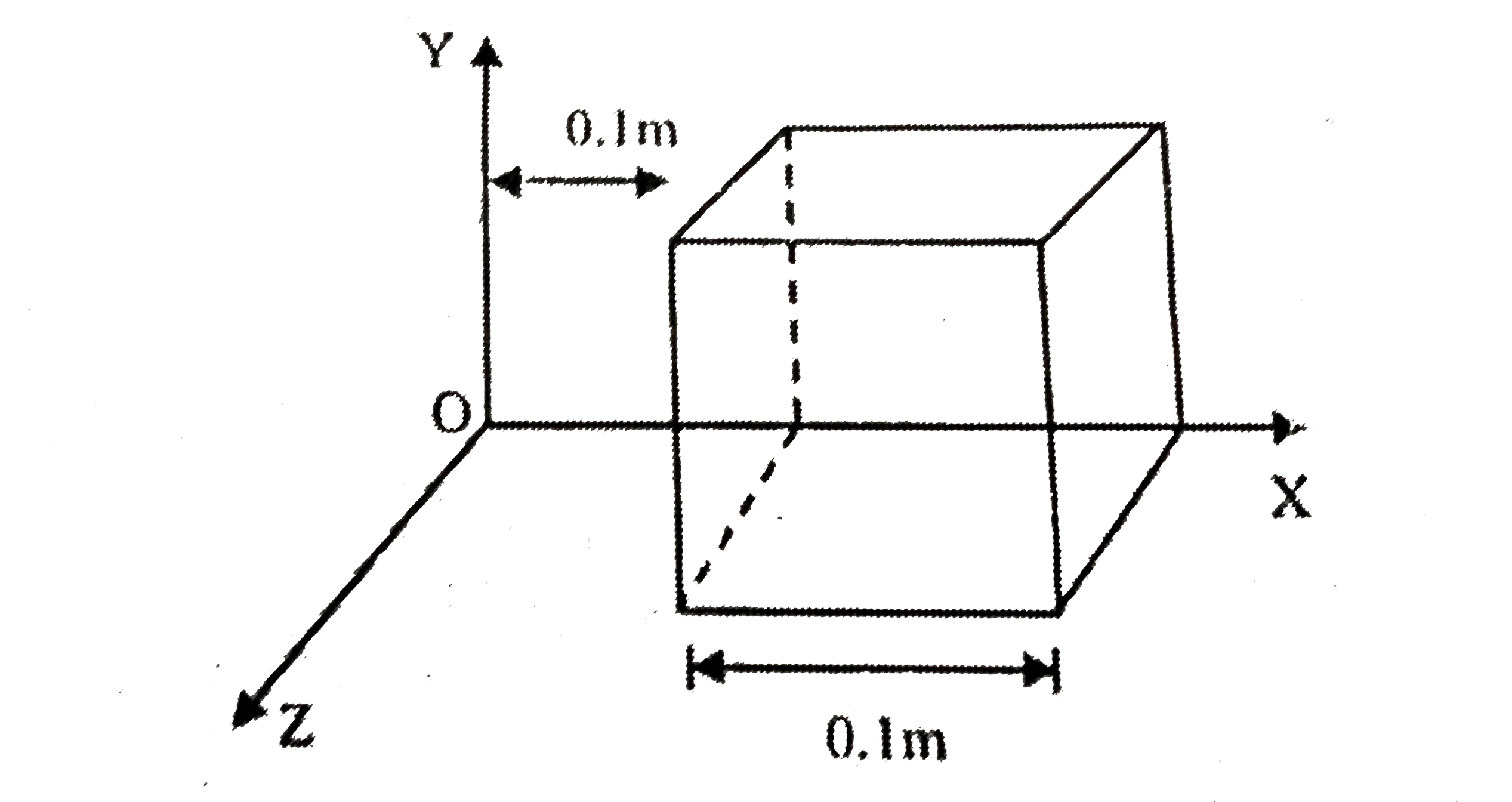 A600μCB60μCC53μCD6μC
A600μCB60μCC53μCD6μC - Question 2 - Select One
Three infinitely long thin conductors are joined at the origin of coordinates and lie along the x-y- and z-axes. A current i flowing along the conductor lying along the x-axis divides equally into the othere two at the origin. The magnetic field at the point (0,-a,0) has magnitude
Aμ0i4πaB3μ0i4√2πaC√5μ0i8πaD√3μ0i2πa - Question 3 - Select One
A cube has sides of length L. It is placed with one corner at the origin ( refer to Fig.2.119). The electric field is uniform and given by →€=−Bˆi+Cˆj−Dˆk , where B,C,andD are positive constants.
The total flux passing through the cube isA(B+C+D)L2B2(B+C+D)L2C6(B+C+D)L2Dzero
A cube has sides of length L=0.2m. It is placed with one corner at the origin as shown in figure. The electric field is uniform and given by E=(2.5N/C)ˆi−(4.2N/C)ˆj. Find the electric flux through the entire cube.
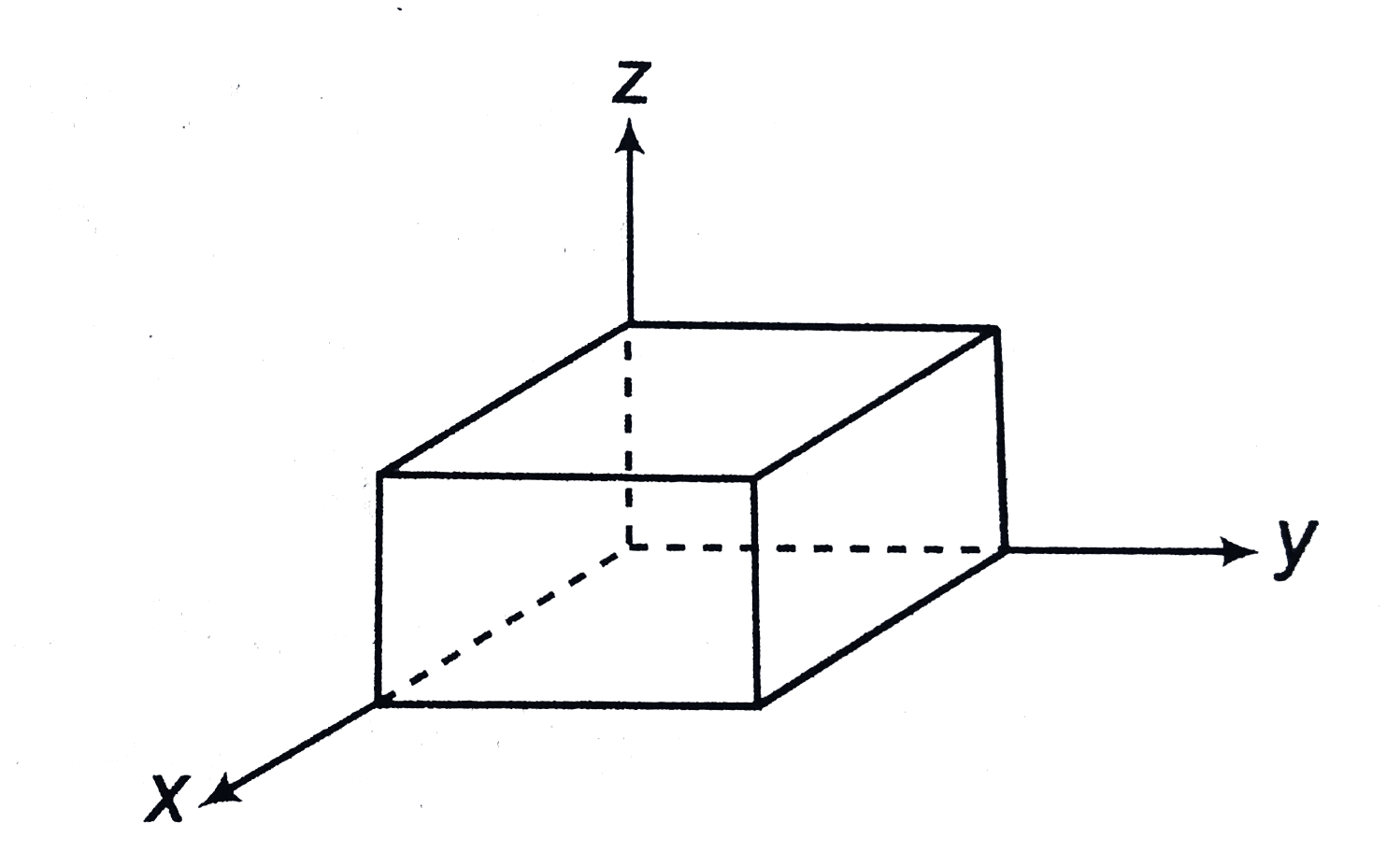 View Solution
View SolutionThe electric fields in a region is given by →E=E0xLˆi ,Find the charge contained inside a cubical volume bounded by the surface x=0,x=L,y=0,y=L,z=0,z=L.
View SolutionA cube is given and it has -q charge in one corner and +q charges in all the remaining 7 corners. Find the electric field at the center of the cube
View SolutionA cube of side b has a charge g at each of its vertices. Determine the potential and electric field due to this charge array at the centre of the cube.
View SolutionA cube of side b has a charge q at each of its vertices. Determine the potential and electric field due to this charge array at the center of the cube.
View Solution

