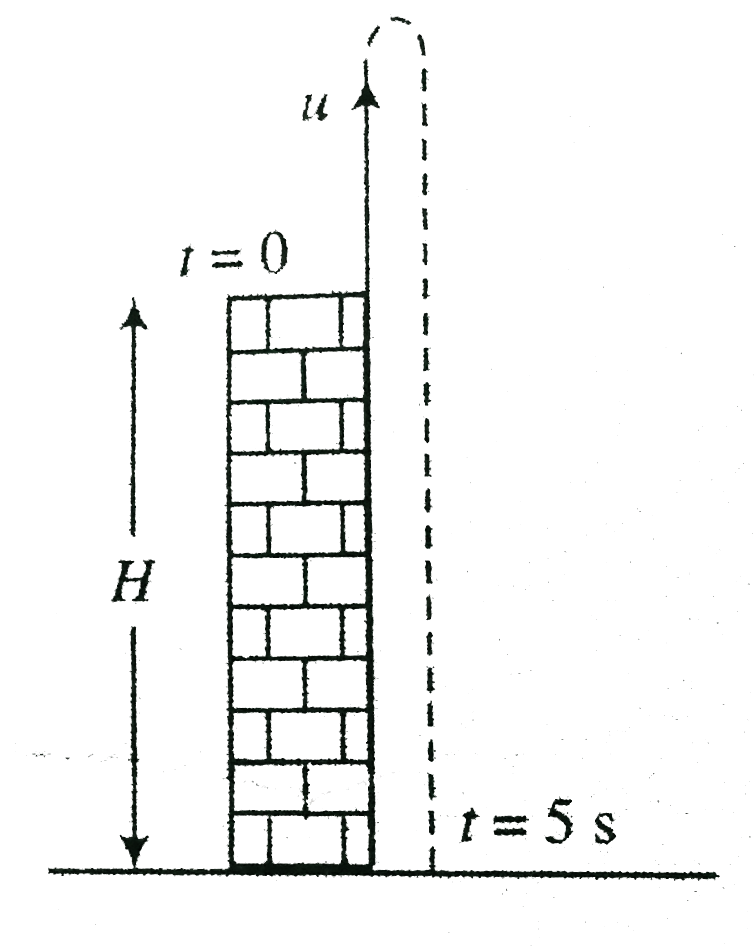
A particle is projected up with initial speed $u = 10 m s^{- 1}$ from the top of a building at time $t = 0$ . At time $t = 5 s$ the particle strikes the ground. Find the height of the building in meter.
.

Text Solution

Verified by Experts

First the particle moes up and reaches to highest point . Then the particle moves downward direction and finally strikes ground aftre $5 s$ .
At highest point the speed of the particle will be zero. Hence, speed is in upward direction and acceleration is in dounward direction. Hence, the sign of acceleration should be negative.
Using $v^{2} = u^{2} + 2 a s$
Hence, $0 = {(10)}^{2} - 2 \times 10 \times H_{1} \Rightarrow H_{1} = 5 m$

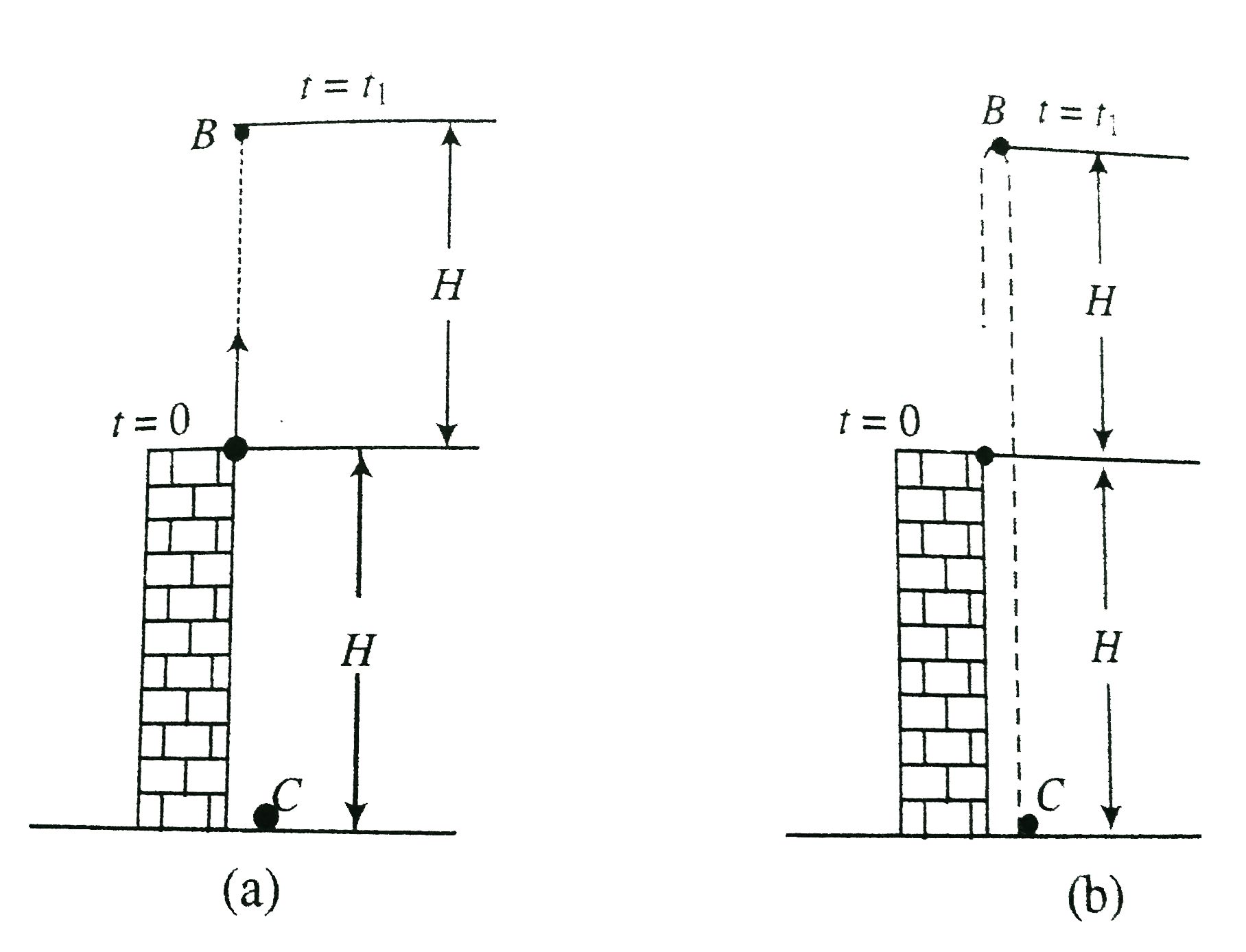
Using $v = u +$ at from $A$ to $B$ ,
$0 = 10 - 10 \times t_{1} \Rightarrow t_{1} = 1 s$
At higherst starts, the particle will be zero. The particle starts moving towards downward directon. Hene the velocity any acceleration both are in downward direction. Hence, the sing of acceleration should be pownward . The time taken by the particle from $B$ to $C$ will be $5 - 1 = 4 s$
Now using $s = u t + \frac{1}{{(2)}^{2}}$ from $B$ to $C$
$(H_{1} + H) = \frac{1}{2} \times 10 \times 4^{2} = 80 m$
$5 + H = 80 m$
$\Rightarrow$ Hence height of the bjjuilding $H = 75 m$
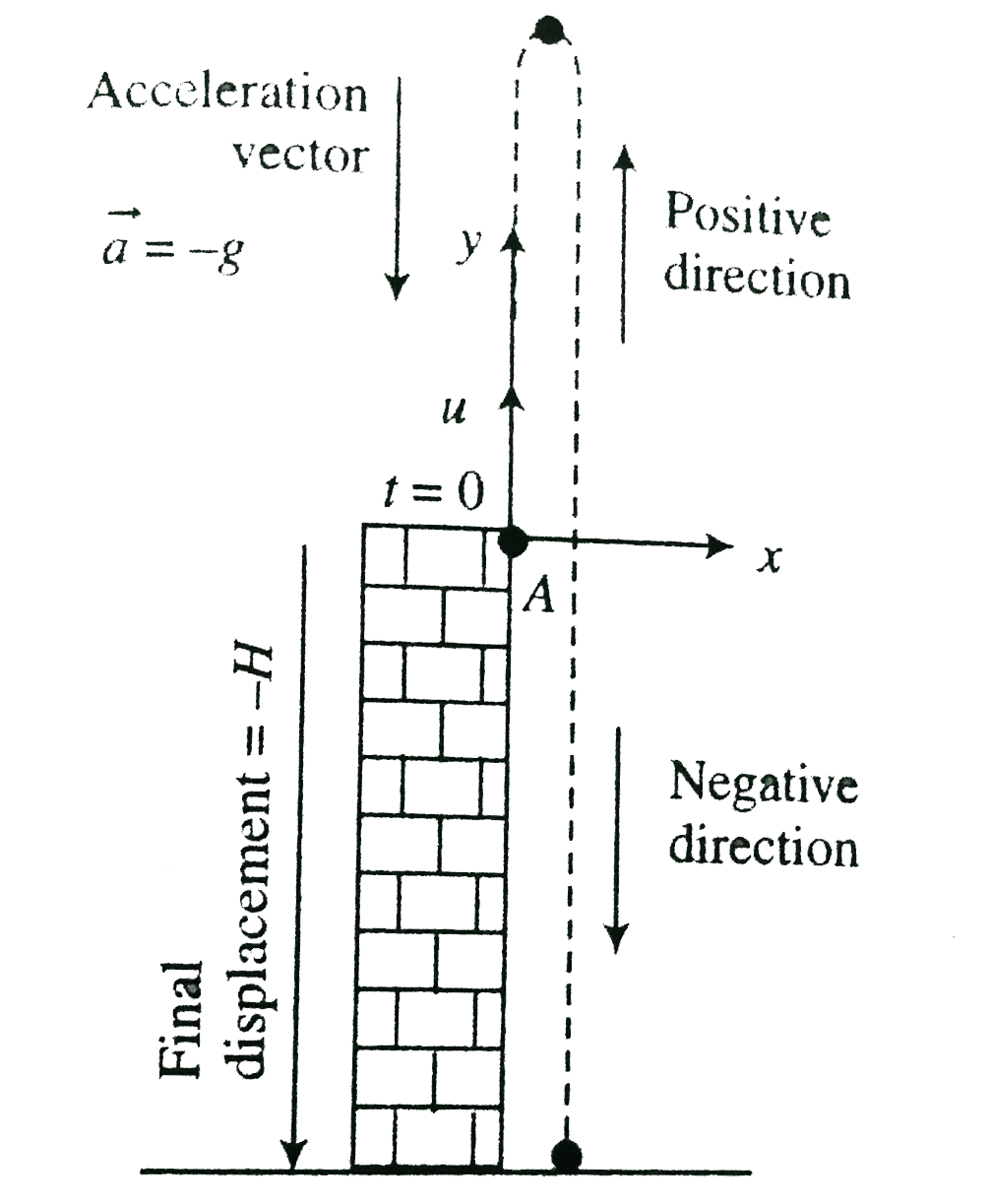
Using vector method
The particle starts from $A$ and finally reaches at $C$ .
Let us take the origin at $A$ . The upward direction is takenas positive and the downward dirction is toaen as netative.
.
The particle moves in gravitational field where acceleration due to gravity is always acting at downward direction whether it is moving upward or downward.
Hence, acceleration vector $\to a$ will always be $- 10 m s^{2}$ , as its marnitude as well as direction remain constant always throughout the motion.
Hence, acceleration $\to a = - 10 m s^{- 2}$
Initially at $t = 0$ , the oartucke is prouected in upward direction.
Hence, initial vellocity $\to u = 10 m s^{- 1}$
The particle moves from $A$ to $B$ (upward) and then $B$ to $C$ (upwnward).
The motion of the particle from $A$ and $B$ then again passes point $A$ . The net displacement of the particle upto this instant is zero. Then particle crosses Point $A$ and finally reaches to $C$ . We know net displacement is wqual to the difference of final position vector and initial postition vector. Hence, net displacemecnt of the particle during motion $t = 5 s$ is $- H m$ .
Using $\to s = \to u t + \frac{1}{2} \to a t^{2}$
$= (10) \times 5 + \frac{1}{2} (- 10) {(5)}^{2} = 50 - 125 = - 75 m$
Hence, $H = 75 m$ .

Updated on:21/07/2023

If a ball is thrown up with a velocity v from the top of a building the ball reaches the ground with a velocity 3u. Find the height of the building.
A $9 u^{2} / g$
B $6 u^{2} / g$
C $4 u^{2} / g$
D $3 u^{2} / g$
A particle is dropped from rest from the top of a building of height 100m. At the same instant another particle is projected upward from the bottom of the building What should be the speed of projection of the particle projected from the bottom of building so that the particle cross each other after 1s? Acceleration due to gravity is 10 $m / s^{2}$ .
A100m/s
B95m/s
C90m/s
D105m/s
A particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle $θ = 37^{\circ}$ to the horizontal $(g = 10 m / s^{2})$

Find the time taken by the particle to hit the plane.
A $\frac{3}{4} s$
B $3 s$
C $4 s$
D $\frac{4}{3} s$