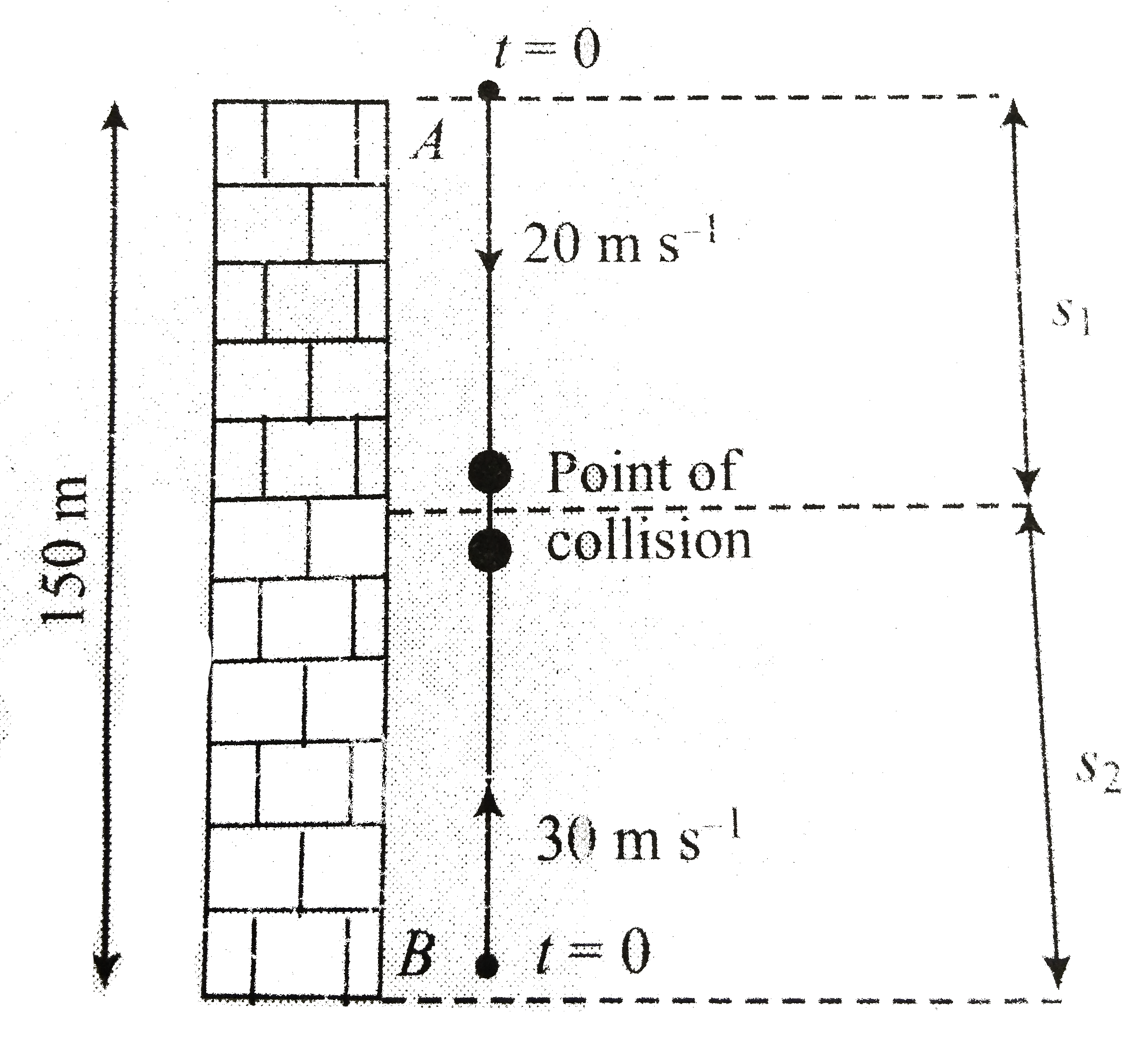
A ball is thrown downwards with a speed of $20 m s^{- 1}$ , from the top of a buling $150 m$ high and simultane-ously another ball is throun vertically upwrds wuth a speed of $30 m s^{- 1}$ from the foot ot the building . Find the time after wguch both the balls will meet. (g=10 m s^(-2))
.

Video Solution

Text Solution

Verified by Experts

Method-1: Let the first ball move distance $S_{1}$ and second ball moves up a distance $S_{2}$ before they meert.
Let us take downward direction as direction as positive.
Then $S_{1} = 20 t + 5 t^{2}$
$S_{2} = 30 t - 5 t^{2}$
But, $S_{1} + S_{2} = 150$
$\Rightarrow 150 = 50 t$
$\Rightarrow t = 3 s$
Method-2: Let us solve this pronlem by using the method of relative velocity .
Relative acceleration of both is zero since both have same acceleration is downward direction.
${\to a}_{A B} = {\to a}_{A} = - {\to a}_{B} = g - g = 0$
Initial relatie velocity,
${\to v}_{B A} = 30 - (- 20) = 50 m s^{- 1}$ .

Updated on:21/07/2023

A ball is thrown horizontally with a speed of $20 m / s$ from the top of a tower of height 100m
Time taken by the ball to strike the ground is
A $\sqrt{20} s$
B $2 \sqrt{20} s$
C $4 \sqrt{20} s$
D $10 s$
A ball is dropped from the top of a building 100 m high. At the same instant another ball is thrown upwards with a velocity of $40 m s^{- 1}$ form the bottom of the building. The two balls will meet after.
A5 s
B2.5 s
C2 s
D3 s
A ball is dropped from the top of a building of height 80 m. At same instant another ball is thrown upwards with speed 50 m/s from the bottom of the building. The time at which balls will meet is
A1.6 s
B5 s
C8 s
D10 s