You are on the roof of the phusics building, 46,0m above the ground (Fig.4.40). Your physics professor, who is 1.80m tall, is walking alongside the bulding at a constant speed of 1.10ms−1. If you wish to drop a flower on your professors head, where should the professor be when you release the flower? Assume that the flower is in free fall.
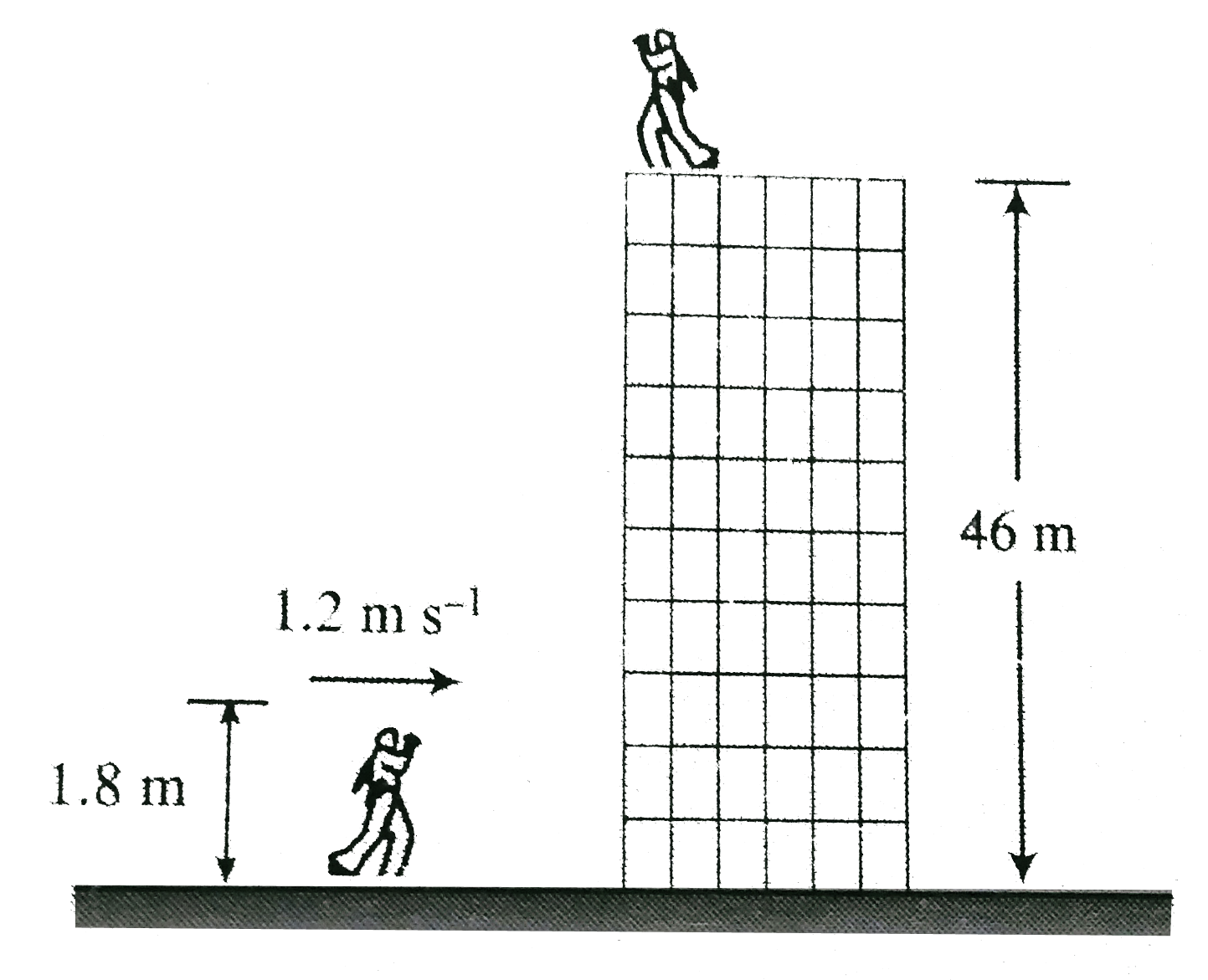 .
.
The time needed for the egg to fall is
t√2Δh9=√2(46.0m−1.89m)(9.80ms−2)=3.00s
and so the professor should be at a distance
vyt=(1.20ms−1)(3.00s)=3.60m.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.315videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.416videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.117videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer9videos
KINEMATICS-2
Similar Questions
You are on the roof of your school building 60m, high. You see your physics teacher 1.6 m tall walking directly towards the building at 2.m/s. You wish to throw an egg vertically down at a speed 5m/s on to your teacher's head. Where should your teacher be when you throw the egg. Neglect air resistance. Take g=10m/s2
View SolutionA skier is pulled by towrope up frictionless ski slope that makes an angle of 12∘ with the horizontal . The rope moves parallel to the slope with a constant speed of 1.0 m/s. The force of the rope does 880 J of work on the skier as the skier moves a distance of 7.0 m up the incline. (a) If the rope moved with a constant speed of 2.0 m/s, how much work would the force of the rope do on the skier as the skier moved a distance of 8.0 m up the incline ? At what rate is the force of the rope doing work on the skier when the rope moves with a speed of (b) 1.0 m/s and (c) 2.0 m/s ?
View Solution
Knowledge Check
- Question 1 - Select One
You step into an elevator, and it accelerates to a downward speed of 9.2 m/s in 2.1 s. How does your apparent weight during this acceleration compare with your actual weight? Apparent weight is
A55% of actualB155% of actualC100% of actualD30% of actual - Question 2 - Select One
A coolie 1.5 m tall raises a load of 80 kg in 2 sec from the ground to his head and then walks a distance of 40 m in another 2 second. The power developed by the coolie is : (g=10m/s2)
A0.2 kWB0.4 kWC0.6 kWD0.8 kW
A ball is thrown straight up from the edge of the roof of a building .A second ball is dropped from the roof 1.00s later. You may ignore air resistance.
a. If the height of the buliding is 20.0m, what must the initial speed be of the first ball if both are to hit the ground at the same time? Consider the same situation, but now let the initial speed v0 of the first ball be given and treat the height (h) of the building as an unknown.
b. What must the height of the building be for both balls to reach the ground at the same time for each of the following values of v0: (i) 6.0ms−1 (ii) 9.5ms−1?
c. If v0 is greater than some values vmax, a value of (h) does same time. Solve for vmax. The value vmin also has a simple physical interpretation. What is it?View SolutionA raindrop of radius 0.2 mm falls through air: If the viscosity of air is 18 ×10−6 Pl, find the viscous drag acting on the drop when its speed is 1 m s−1.
View SolutionA gun fires a large number of bullets upward. Due to shaking of hands some bullets deviate as much as 1° from the vertical. The muzzle speed of the gun is 150m/s and the height of gun above the ground is negligible. The radius of the head of the person firing the gun is 10cm. You can assume that acceleration due to gravity is nearly constant for heights involved and its value is g=10m/s2. The gun fires 1000 bullets and they fall uniformly over a circle of radius r. Neglect air resistance. You can use the fact sinθ≅θ when θ is small.
(a) Find the approximate value of r. (b) What is the probability that a bullet will fall on the person’s head who is firing?View SolutionA steel ball is dropped from th roof of a building. A man standing in front of a 1−m high window in the building notes tha the ball takes 0.1s to the fall from the top to the boottom of the window. The ball continues to fall and strikes the ground. On striking the ground, the ball gers rebounded with the same speed with which it hits the ground. If the ball reappears at the bottom of the window 2s after passing the bottom of the window on the way down, dind the height of the building.
View SolutionA moving sidewalk in an airport terminal building moves at a speed of 1.0ms−1 and is 35.0m relative to the moving sidewalk, then find the time that she requires to reach the opposite end a when she walks in the same direction the sidewalk is moving and b when she walks in the opposite derection.
View SolutionA ball (A) is thrown straight upfrom the edge the roof of a building. Another ball (B) is dropped from the of 1.00s later. You may ignore air resistance . (a) If the height of the building id 20.0m, what must the initial speed of ball (A) he if bothe are to hit the ground at the same time? (b) On the function of time, measured fro when the first ball is thrown and take origin at ground.
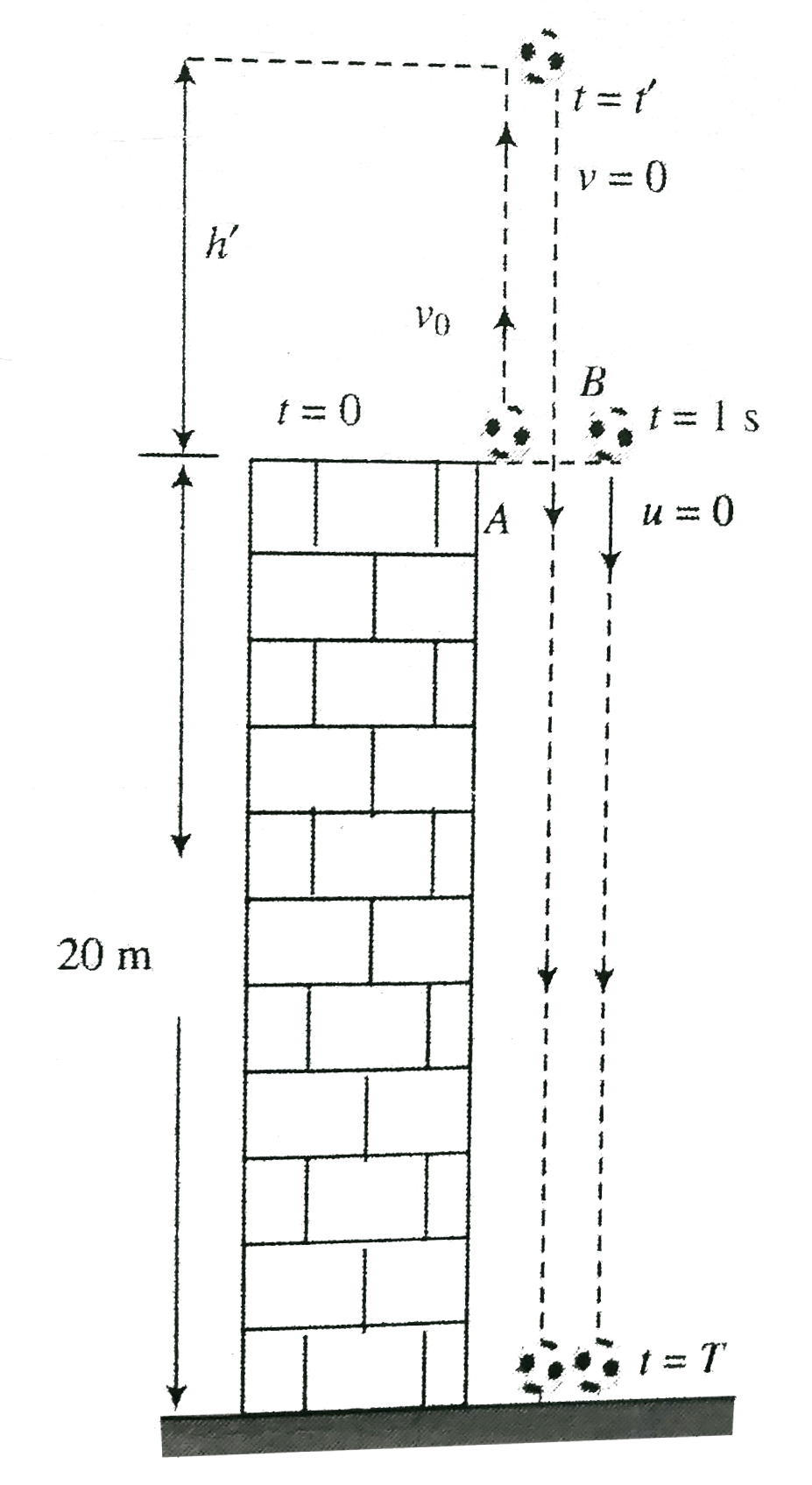 .View Solution
.View Solution

