(a) In which direction should the motorboat given in Illustration head in order to reach a point on the opposite bank directly east from the starting point ? The boat's speed relative to the water remains .
(b) What is the velocity of the boat relative to the earth ?
( c) How much time is required to cross the river ?
As the boat has to each exact opposite end to the point of start, the boat has to start (velocity ) at an angle aiming somewhat upstream. Taking into count the push given by the current,
Velocity of boat w.r.t. river,
Velocity of river w.r.t. Earth,
velocity of boat w.r.t. Earth,
(a) To find the direction of the boat in which the boat has to go,we need to find angle .
From
Hence, the motorboat has to head at north of east.
(b) To find the velocity of boat w.r.t. Earth, we can use pythagorous theorem again.
Fro , we have
( c) Time taken to cross the river is
(Width of river)/(Velocity of boat w.r.t Earth)
.
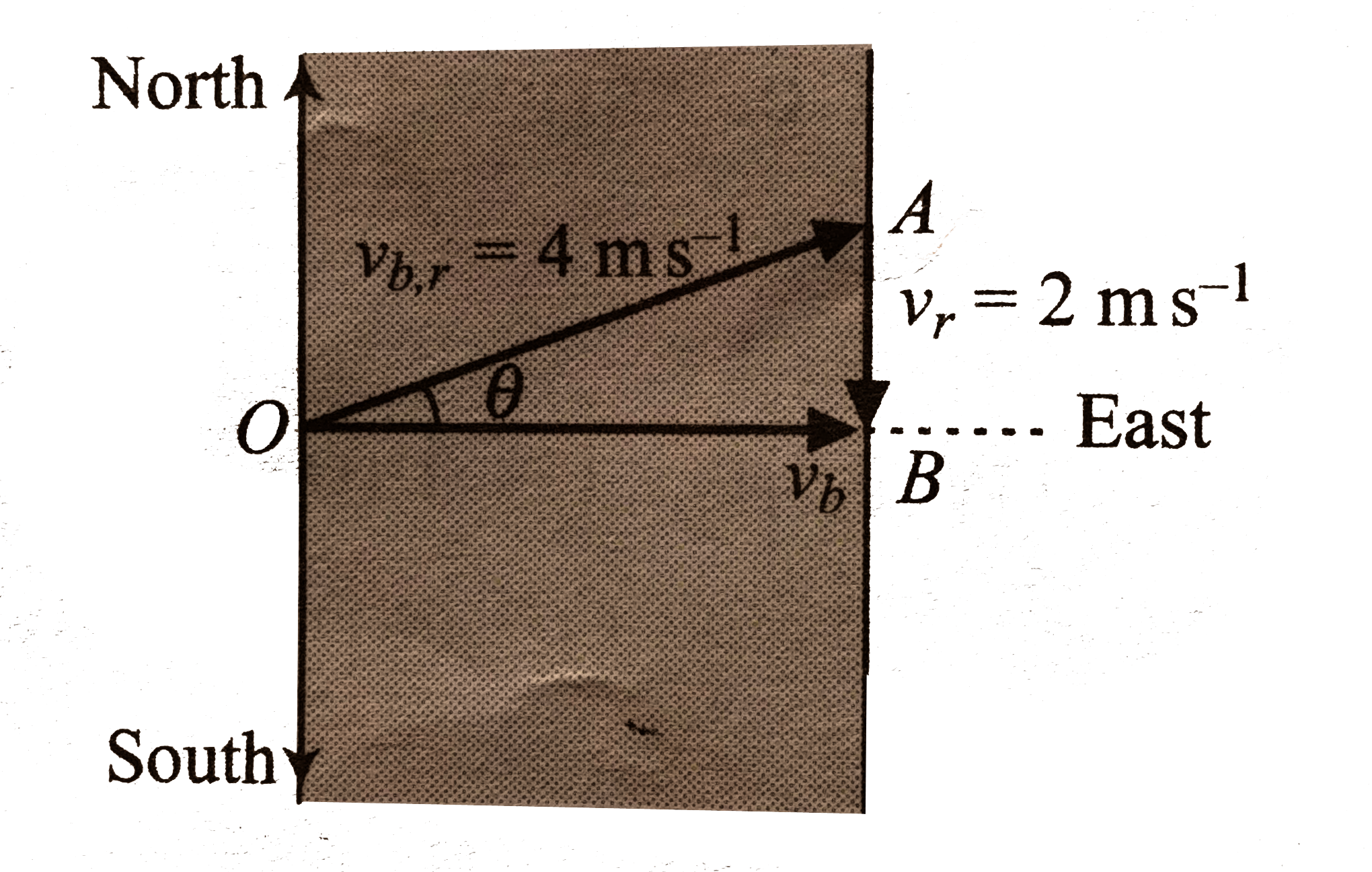 .
.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Solved Examples
7 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.1
15 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
A river flows due south with a speed of 2.0ms−1. A man strees a motorboat across the river , his velocity relative to the water is 4ms−1 due east. The river is 800m wide.
(a) What is his velocity (magnitude and direction) relative to the earth ?
(b) How much time is required to cross the river ?
( c) HOw far south of his starting points will he reach the opposite bank ?
View SolutionA river flows due south with a speed of 2.0ms−1. A man strees a motorboat across the river , his velocity relative to the water is 4ms−1 due east. The river is 800m wide.
(a) What is his velocity (magnitude and direction) relative to the earth ?
(b) How much time is required to cross the river ?
( c) HOw far south of his starting points will he reach the opposite bank ?
View Solution
Knowledge Check
A man wants to reach point B on the opposite bank of a river flowing at a speed 4m/s as shown in the figure. What minimum speed relative to water should the man have so that he can reach point B directly by swimming?
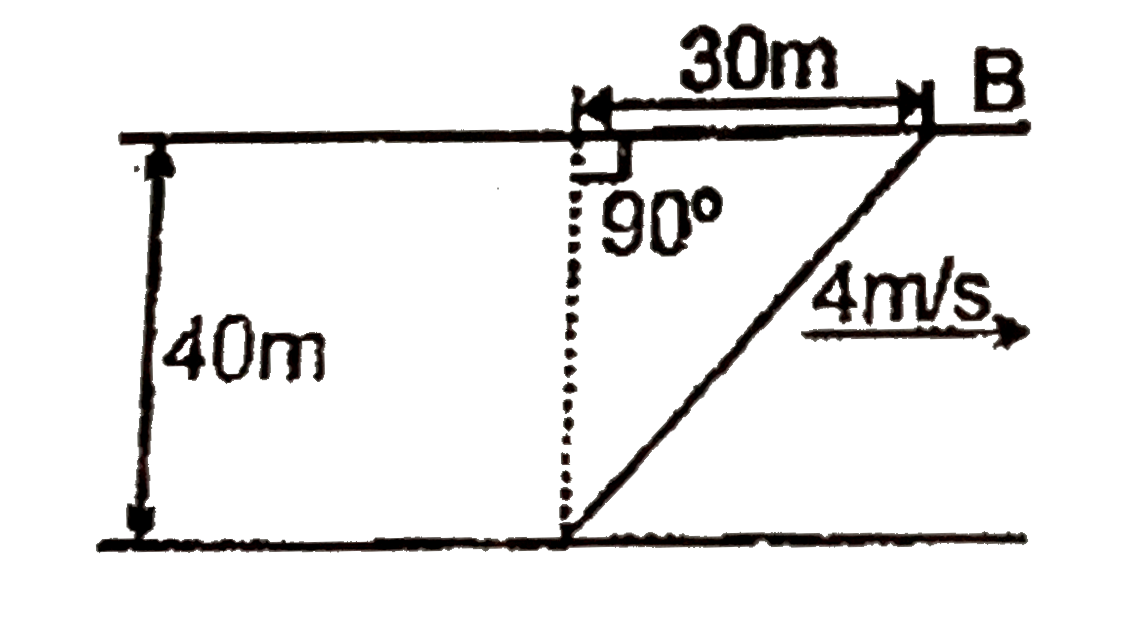 A8m/sB3.2m/sC6.5m/sD7√2m/s
A8m/sB3.2m/sC6.5m/sD7√2m/s
Two ports, A and B, on a north-south line ar separated by a river of width D. The river flows east with speed u. A boat crosses the river starting from port A. The speed of the boat relative to the river is v. Assume v=2u
Q. What is the direction of the velocity of boat relative to river θ, sothat it crosses directly on a line from A to B?A30∘ west of northB30∘ east of northC60∘ west of northD60∘ east of north
A man can row a boat with 4km/h in still water, if he is crossing a river where the current is 2 km/h.
(a) In what direction will his boat be holded, if he wants to reach a point on the other bank, directly opposite to starting point?
(b) If width of the river 4km, how long will the man take to cross the river, with the condition in part (a)?
(c) In what direction shou ld he heat the boat if he wants to cross the river in shorest time and what is this minimum time?
(d) How long will it take him to row 2 km up the stream and then back to his starting point?
View SolutionA man can row a boat with 4km/h in still water, if he is crossing a river where the current is 2 km/h.
(a) In what direction will his boat be holded, if he wants to reach a point on the other bank, directly opposite to starting point?
(b) If width of the river 4km, how long will the man take to cross the river, with the condition in part (a)?
(c) In what direction shou ld he heat the boat if he wants to cross the river in shorest time and what is this minimum time?
(d) How long will it take him to row 2 km up the stream and then back to his starting point?
View SolutionA man wants to reach point B on the opposite bank of a river flowing at a speed u as shown in (Fig. 5.193). What minimum speed relative to water to water should the man have so that he can reach directly to point B ? In which direction should he swim ?
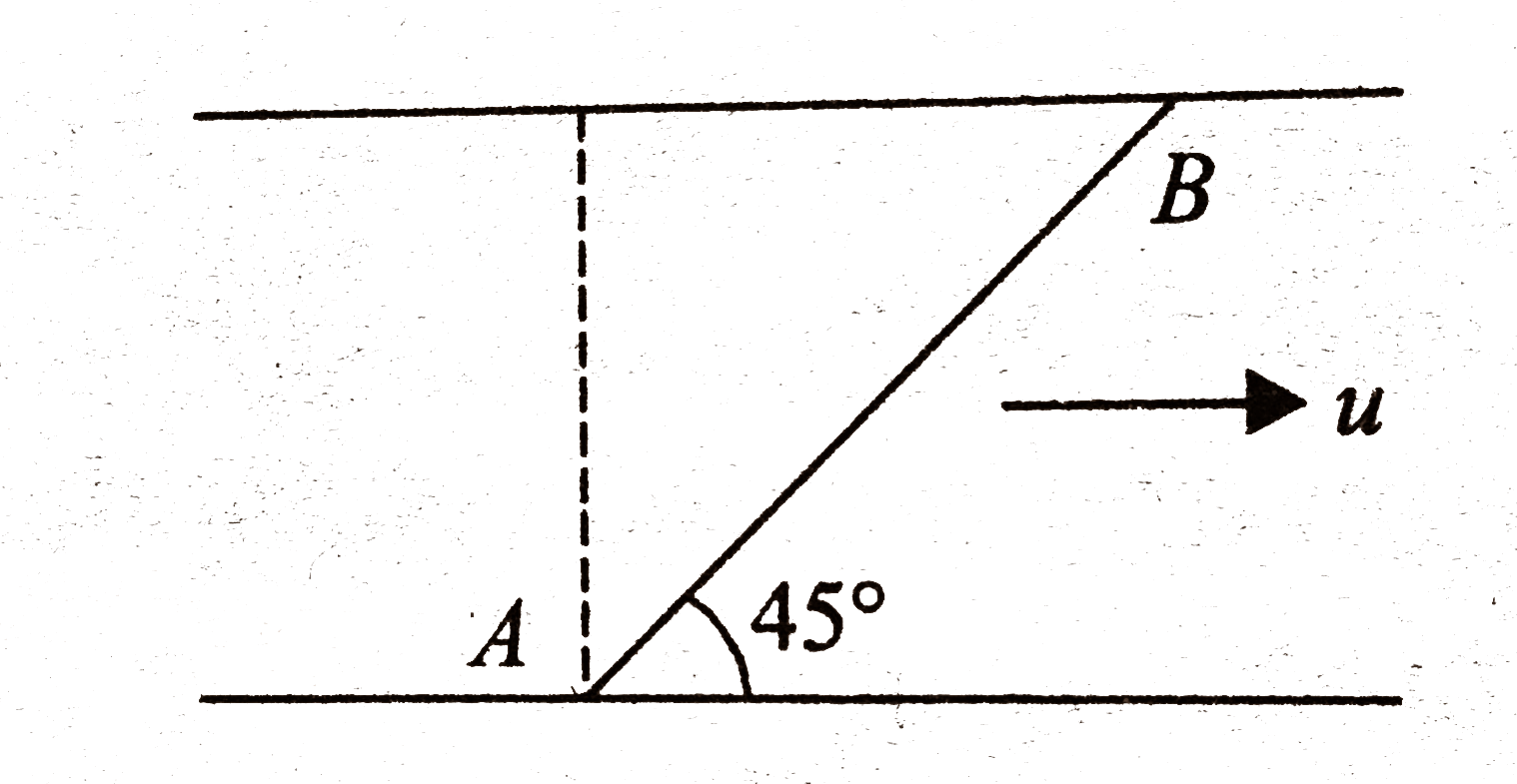 .
.
View SolutionGiven |Vbr|=4m/s= magnitude of velocity of boatman with respect to river, vr=2m/s in the directior shown. Boatman wants to reach from point A to point B. At what angle θ should he row his boat ?
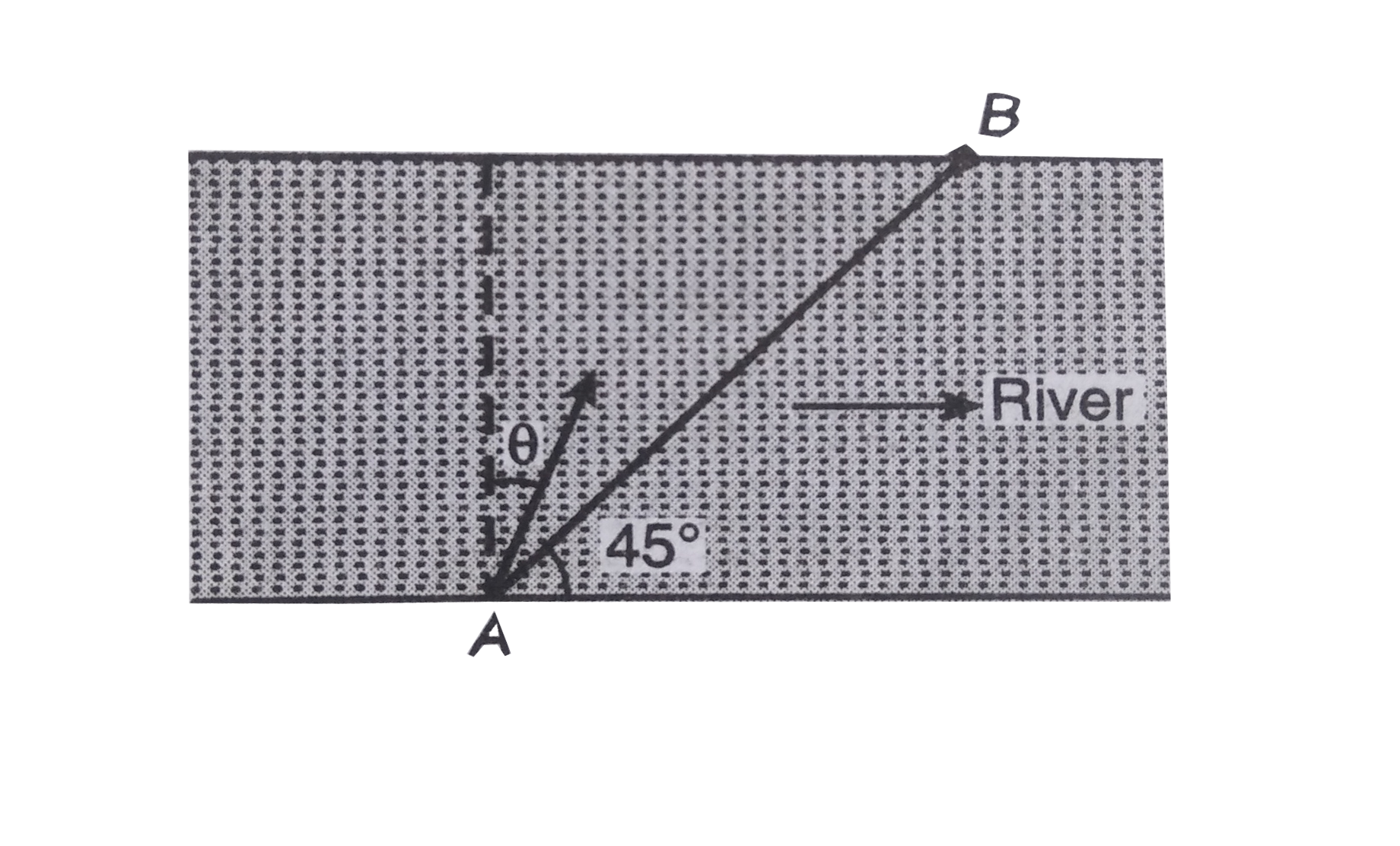
View SolutionA man wants to reach point B on the opposite bank of a river flowing at a speed as shown in figure. What minimum speed relative to water should the man have so that he can reach point B? In which direction should he swim?
View SolutionA man wants to reach point B on the opposite bank of a river flowing at a speed as shown in figure. What minimum speed relative to water should the man have so that he can reach point B? In which direction should he swim?
View Solution
