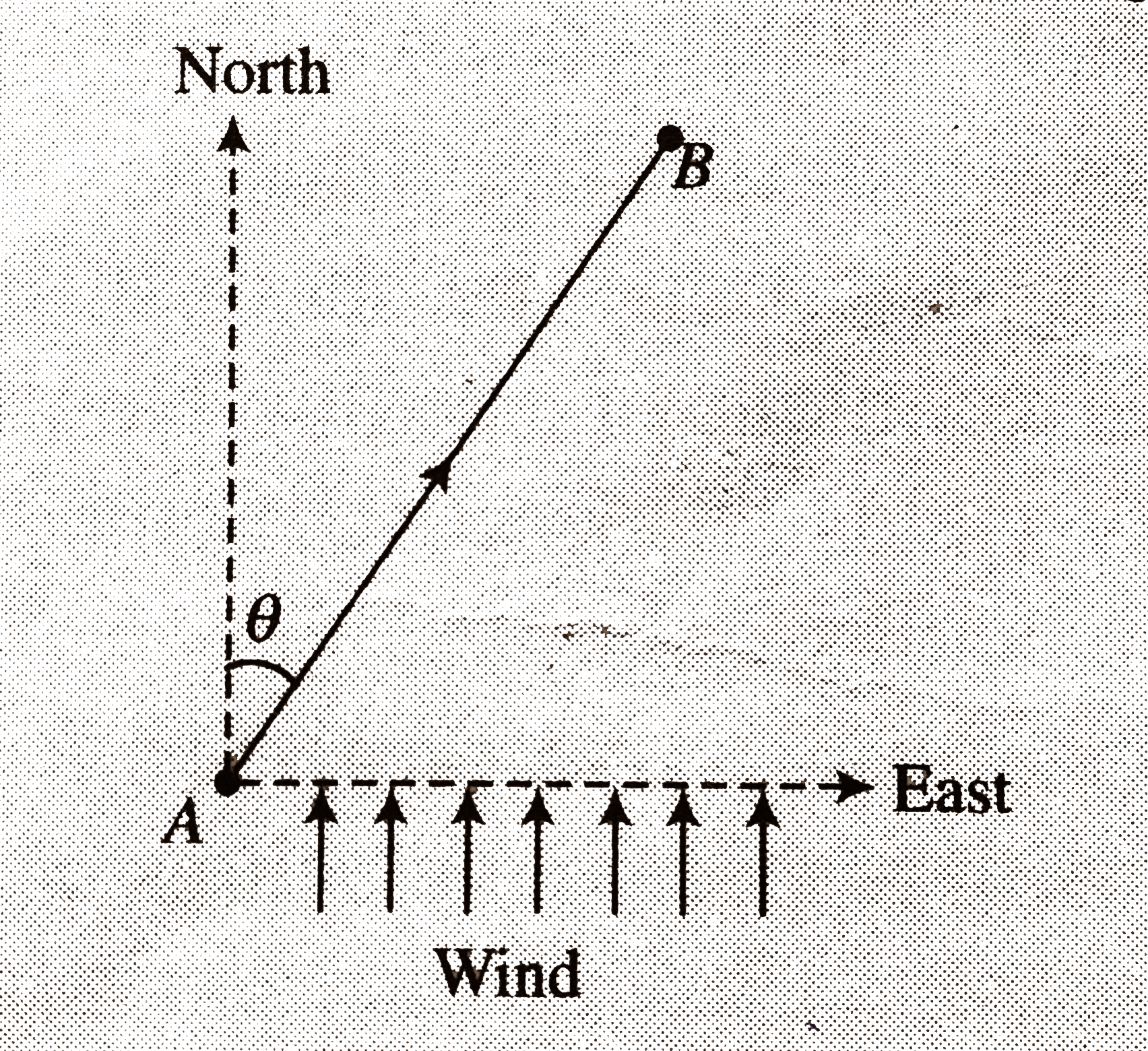
A helicopter files horizontally with constant velocity in a direction $θ$ east of north between two points $A and B$ , at distance $d$ apart. Wind is blowing from south with constant speed $u,$ the speed of helicopter relative to air is $n$ $u$ where $n > 1$ . find the speed of the helicopter along $A B$ . The helicopter returns from $B$ to $A$ with same speed nu relative to air in same wind. Find the total time for the journeys.
.

Text Solution

Verified by Experts

Velocity of helicopter w.r.t. groundn is given by
${\to V}_{H e l i c o p t e r, a i r} = {\to V}_{H e l i c o p t e r, a i r} + {\to V}_{A i r} = {\to V}_{A i r} + {\to V}_{H e l i c o p t e r, a i r}$
$∣ ∣ {\to V}_{H A} ∣ ∣ = n u, ∣ ∣ {\to V}_{A} ∣ ∣ = u, ∣ ∣ {\to V}_{H} ∣ ∣ = V$
Hence, the actual velocity of helicopter is the vector sum of its velocity of helicopter relative to air and velocity of air.
Using cosine rule, for motion from $A \to B$ ,
$n^{2} u^{2} = u^{2} + v^{2} - 2 u v cos θ$
or $v^{2} - 2 u v cos θ = u^{2} (n^{2} - 1)$
or ${(v - u cos θ)}^{2} = u^{2} (n^{2} - 1) + u^{2} {cos}^{2} θ$
= $u^{2} (n^{2} - {sin}^{2} θ)$
$v - u cos θ = \pm u \sqrt{n^{2} - {sin}^{2} θ}$
$v = u cos θ \pm u \sqrt{n^{2} - {sin}^{2} θ}$
As $n \geq 1$ ,
$n^{2} - {sin}^{2} θ \geq 1 - {sin}^{2} θ \geq {cos}^{2} θ$
Hence, speed of helicoper is $v = u cos θ + u \sqrt{n^{2} - {sin}^{2} θ})$
Now we consider motion from $B$ to $A$ .
Similar to first case, the helicopter will return to $A a l o n g B A$ when its velocity after being deflected by wind is along $B A$ .
Once again using consine rule inthe vector triangle, we get
$n^{2} u^{2} = u^{2} + V^{2} - 2 u V cos (180^{\circ} - θ)$
= $u^{2} + V^{2} + 2 u V cos θ$
$V = - u cos θ + u \sqrt{n^{2} - {sin}^{2} θ}$
The total time for motion $A$ to $B$ and $B$ to $A$ ,
$t = \frac{d}{v} + \frac{d}{V}$
= $\frac{d (u + V)}{u V}$
= $\frac{2 d u \sqrt{n^{2} - {sin}^{2} θ}}{u^{2} (n^{2} - {sin}^{2} θ) - u^{2} {cos}^{2} θ}$
= $\frac{2 d u \sqrt{n^{2} - {sin}^{2} θ}}{u^{2} (n^{2} - 1)} = \frac{2 d \sqrt{n^{2} - {sin}^{2} θ}}{u (n^{2} - 1)}$ .
, .

Updated on:21/07/2023

|

Class 11 PHYSICS PROJECTILE MOTION

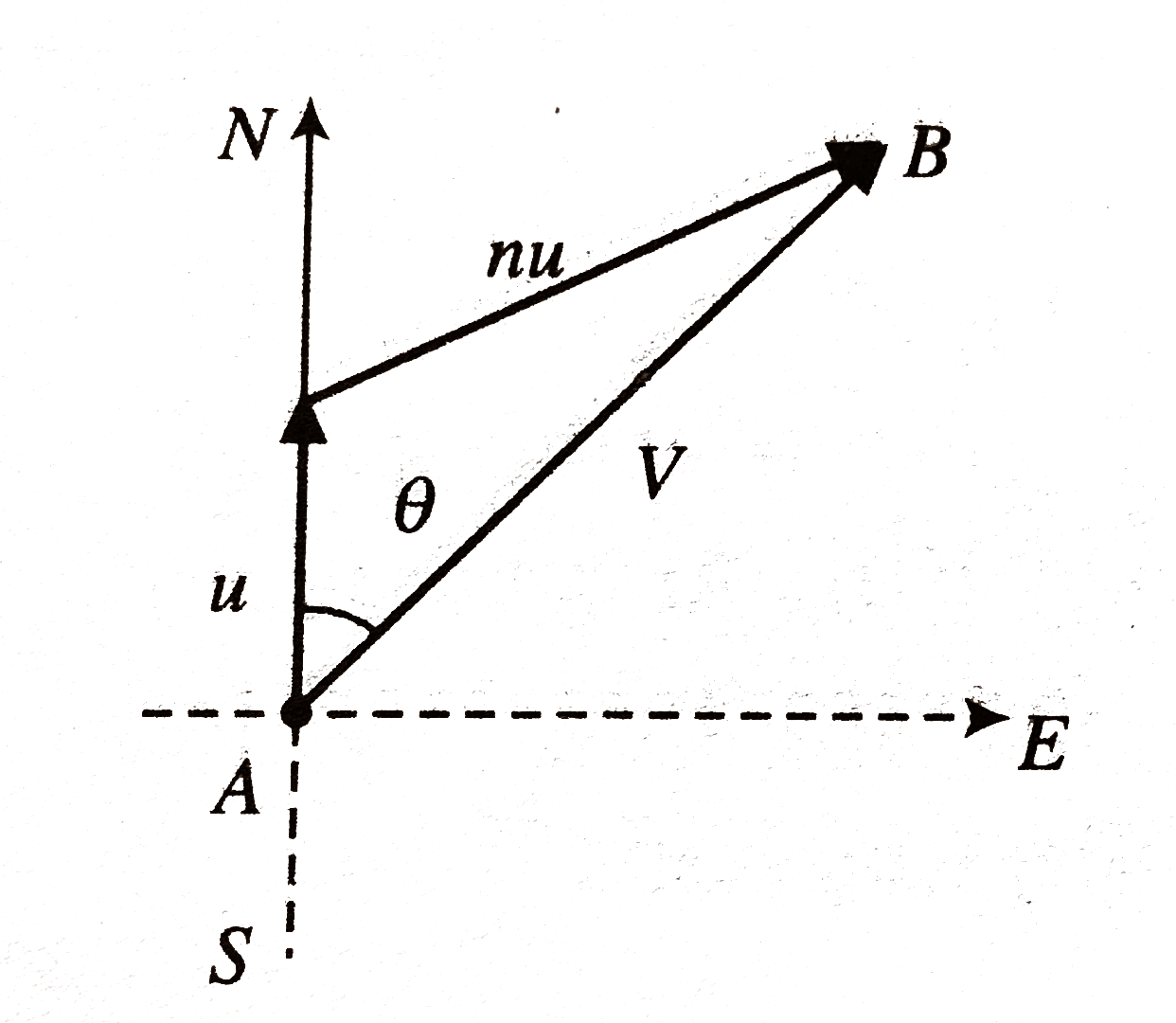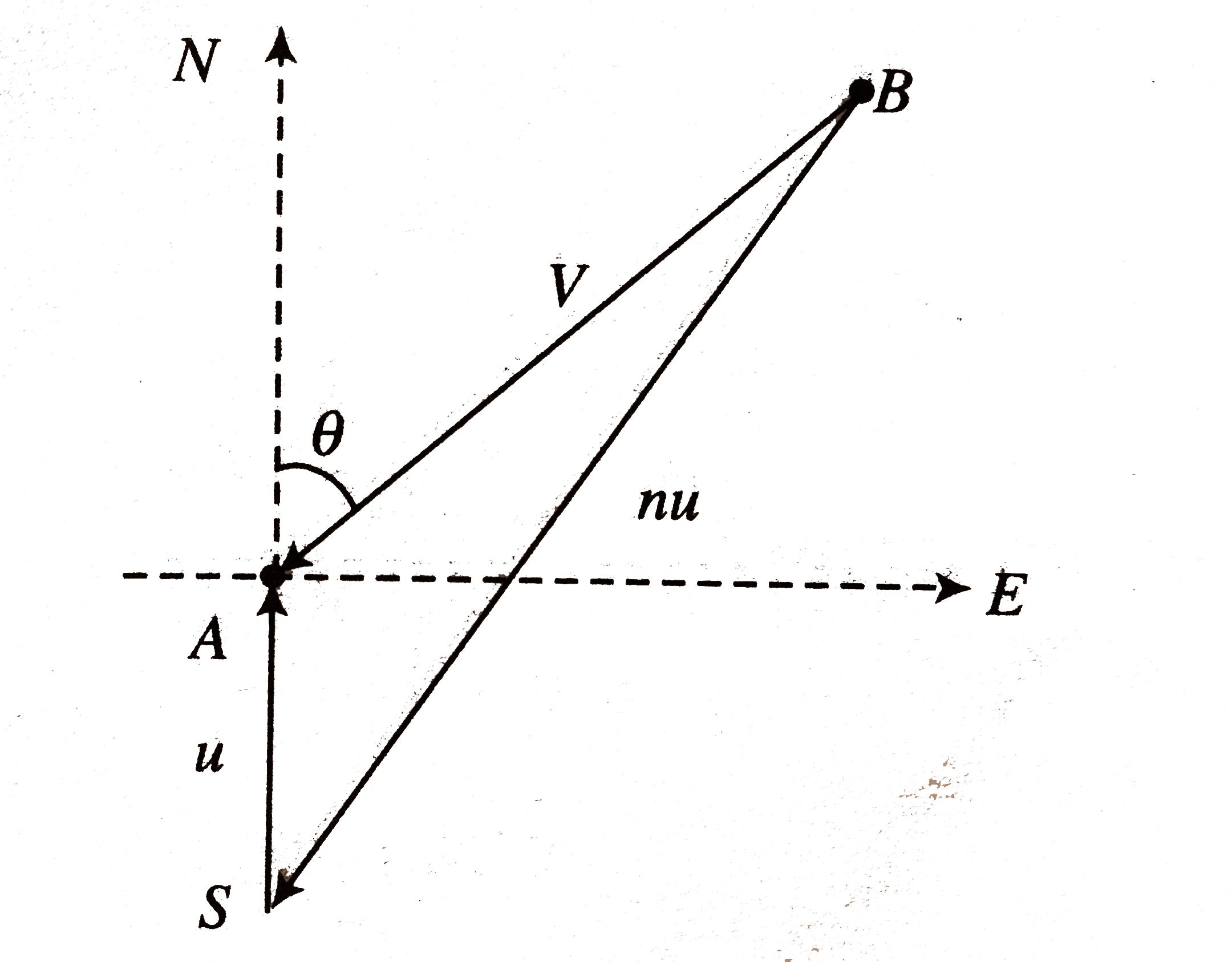Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS-KINEMATICS-2-Exercise Integer

Home
Ask Doubt
Profile