A particle is projected at angle θ with horizontal with velocity v0att=0. Find
(a) tangential and normal acceleration of the particle at t=0 and at highest point of its trajectory.
(b) the radius of curvature a=0 and highest point.
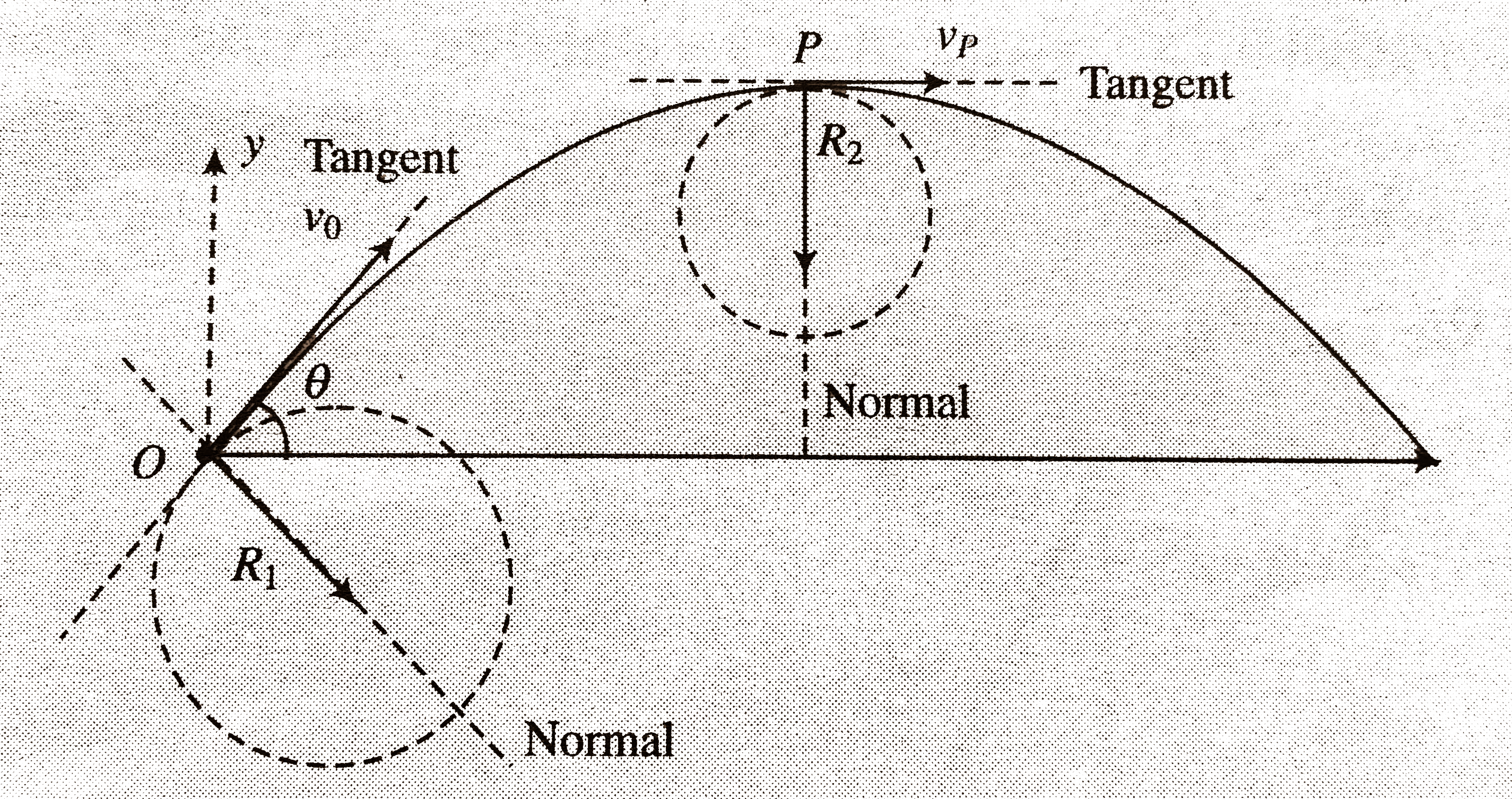 .
.
(a) The direction of tangential acceleration is in the line of velocity and the direction perpendicular to velocity direction. The tangential and normal directions at OandP are shown in (Figs. 161 and 5.162), respectively.
The net acceleration of the particle during motion is acceleration due to gravity, i.e., g is acting vertically downward.
At O(att=0) :
Tangential acceleration,
at=−gsinθ
Normal acceleration,
an=gcosθ
At P(at highest point) :
Tangential acceleration,
at=0andan=g
(b) Let the radius of curvature at O be R0. The normal acceleration at Obegcosθ.
an=v2R⇒R0=v20an=v20gcosθ
Radius of curvature at P :
Normal acceleration at P is g. Hence,
RP=v2an=(v0cosθ)2g=v20cos2θg.
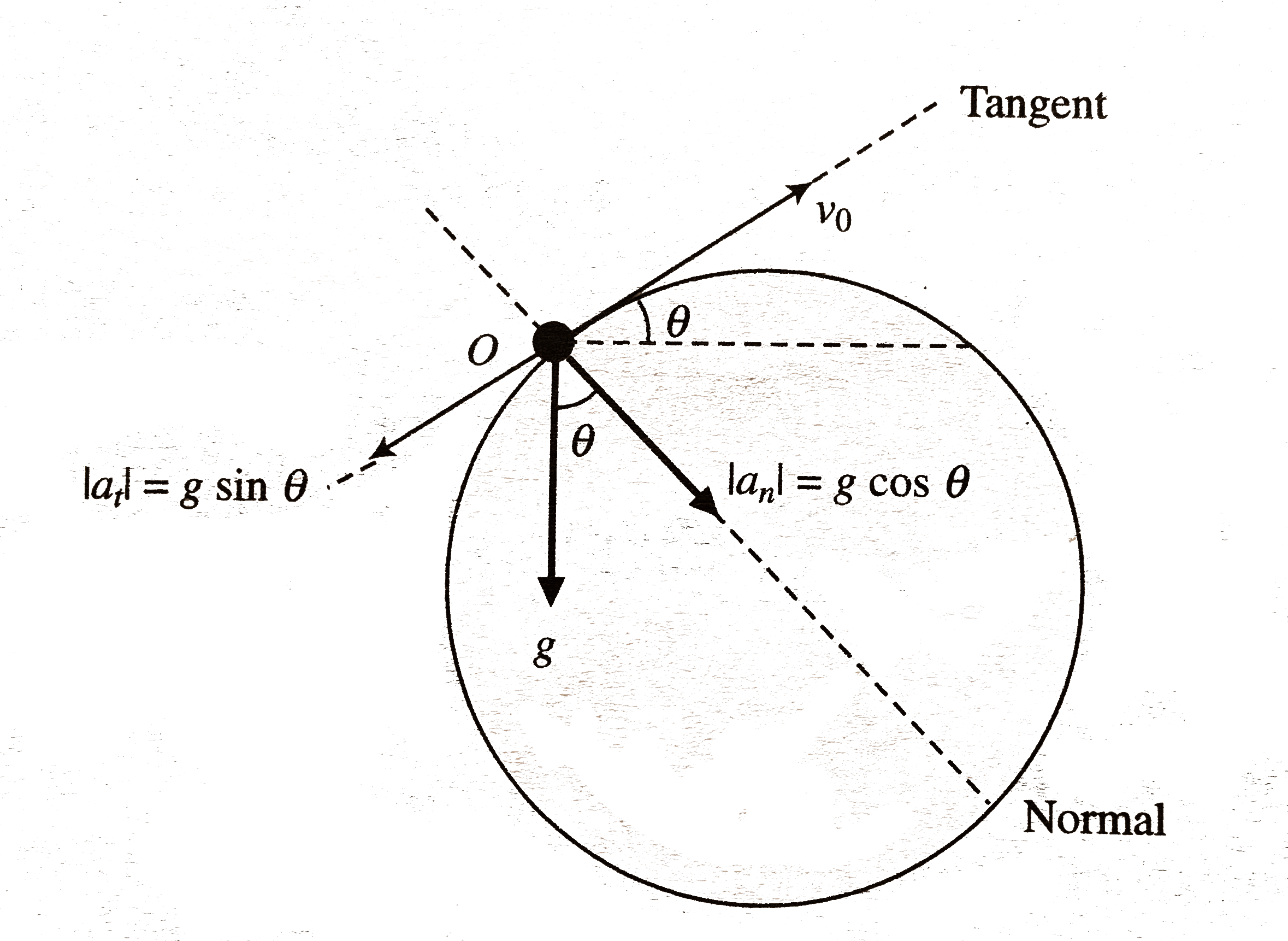 ,
,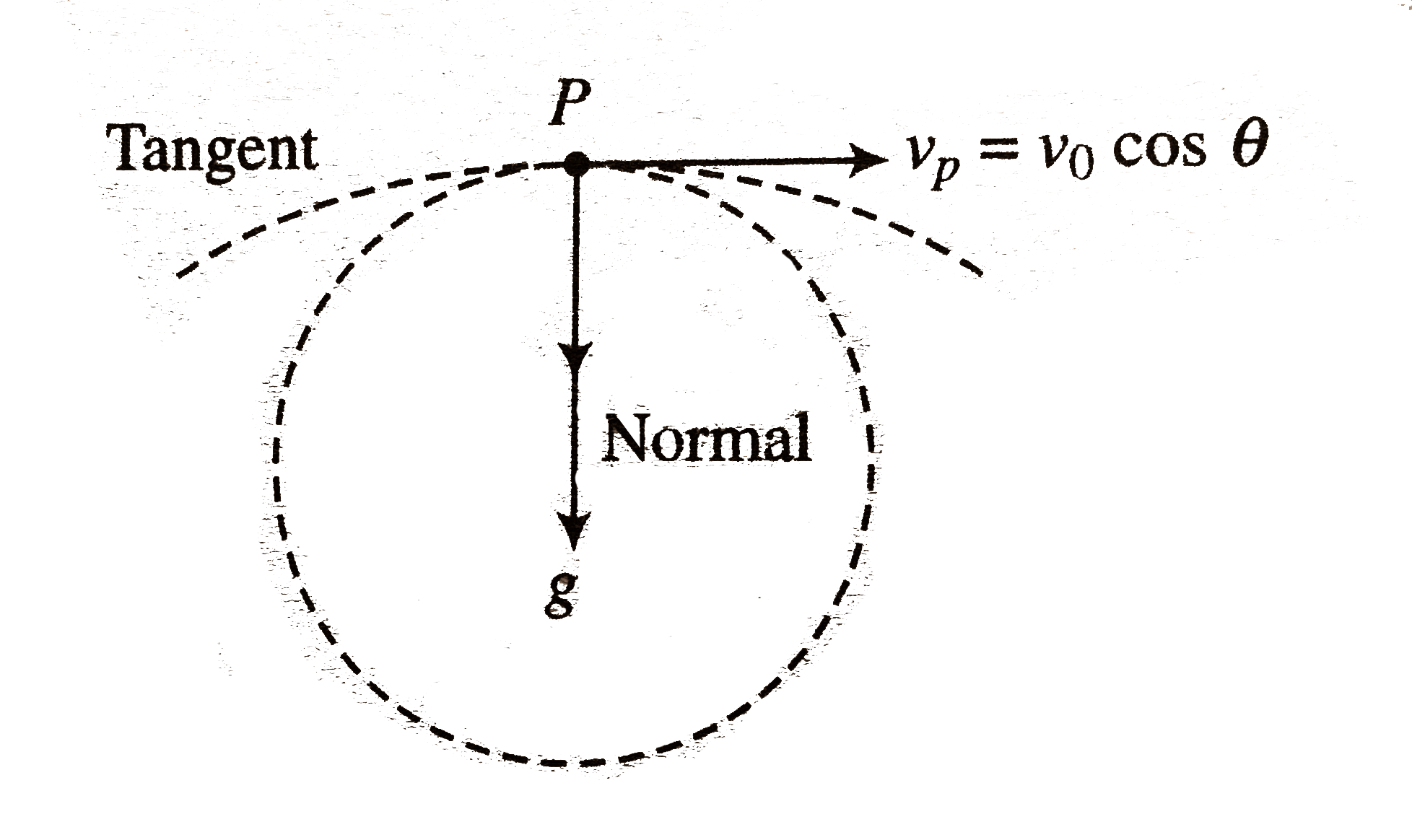 .
.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Solved Examples7videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.115videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
Similar Questions
A paricle is projected at an anged θ from the horizontal with kinetic energy (T). What is the kinetic energy of the particle at the highest point ?
View SolutionA particle is projected with velocity 20√2m/s at 45∘ with horizontal. After 1s , find tangential and normal acceleration of the particle. Also, find radius of curveture of the trajectory at that point. (Take g=10m/s2)
View Solution
Knowledge Check
- Question 1 - Select One
Acceleration of a particle under projectile motion at the highest point of its trajectory is :
AgBzeroCless than gDdependent upon projection velocity - Question 2 - Select One
A particle is projected at t=0 with velocity u at angle θ with the horizontal. Then the ratio of the tangential acceleration and the radius of curvature at the point of projection is :
Ag2sin2θu2B2g2sinθu2Cg2sinθu2Dg2sin2θ2u2 - Question 3 - Select One
A psrticle is projected at t=0 with velocity u at angle θ with the horizontal. Then the ratio of the tangential acceleration and the radius of curvature at the point of projection is :
Ag2sin2θu2B2g2sinθu2Cg2sinθu2Dg2sin2θ2u2
A particle of mass m is projected with velocity v at an angle θ with the horizontal. Find its angular momentum about the point of projection when it is at the highest point of its trajectory.
View SolutionA particle of mass m is thrown with speed v0 at angle 30∘ with horizontal. Find the angular momentum about the point of projection when the particle is at the highest point of its trajectory.
View SolutionA body is projected at angle of 45∘ to the horizontal . What is its velocity at the highest point ?
View SolutionA particle projected with velocity u at angle θ with horizontal at t=0. What is the magnitude of change in the velocity of the particle when it is at maximum height?
View SolutionWhen a projectile is at the highest point of its trajectory, the directions of its velocity and acceleration are
View Solution

