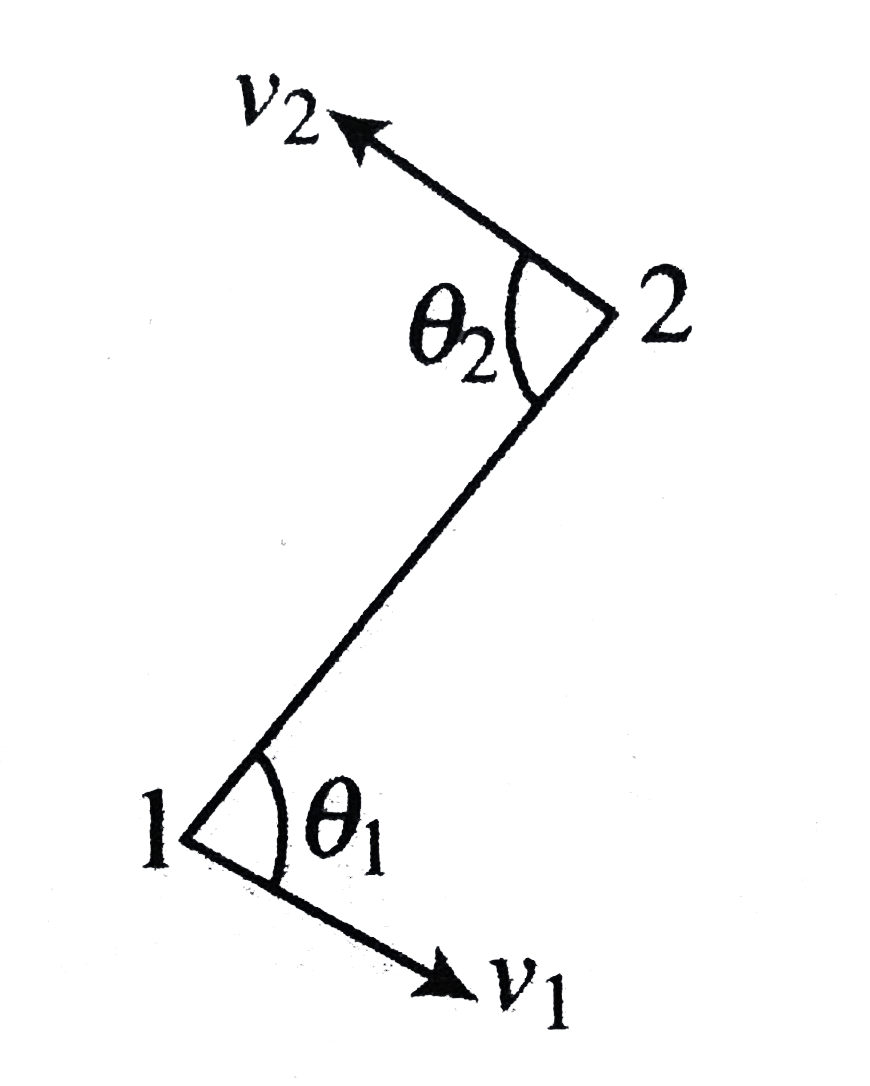
Two particles $1 and 2$ move with velocities ${\to v}_{1}$ and ${\to v}_{2}$ making the angles $θ_{1} and θ_{2}$ with the line joining them, respectively. Find angular velocity of $r e l a t i v e \to 1$ .
.

Video Solution

Text Solution

Verified by Experts

Let us find the relative velocity between the particles perpendicular to the line joining them, the velocity of $1$ relative to velocity of $2$ is
${\to v}_{12} = {\to v}_{1} - {\to v}_{2}$
Then, ${\to v}_{12_{y}} = {\to v}_{1_{y}} - {\to v}_{2_{y}} = - v_{1} {sin θ}_{1} ˆ j - v_{2} {sin θ}_{2} ˆ j$
Hence, $ω_{12} = \frac{∣ ∣ {\to v}_{12_{y}} ∣ ∣}{l}$
Substituting $∣ ∣ {\to v}_{12_{y}} ∣ ∣$ , we have
$ω_{12} = \frac{v_{1} {sin θ}_{1} + v_{2} {sin θ}_{2}}{l}$ .
,.

Updated on:21/07/2023

If two bodies are in motion with velocity ${\to v}_{1}$ and ${\to v}_{2}$ :
A $| v_{rel} | = \sqrt{v_{1}^{2} + v_{2}^{2}}$
B $| \to - - - (rel) | = v_{1} \pm v_{2} ∣$
C $v_{re} = 0$
D $v_{rel} > c$ (speed of light)
Two particle A and B, move with constant velocities $\to v_{1} and \to v_{2}$ . At the initial moment their position vectors are $\to r_{1}$ and $\to r_{2}$ respectively . The condition for particles A and B for their collision is
A $\to r_{1} \times \to v_{1} = \to r_{2} \times \to v_{2}$
B $\to r_{1} - \to r_{2} = \to v_{1} - \to v_{2}$
C $\frac{\to r_{1} - \to r_{2}}{∣ ∣ \to r_{1} - \to r_{2} ∣ ∣} = \frac{\to v_{2} - \to v_{1}}{∣ ∣ \to v_{2} - \to v_{1} ∣ ∣}$
D $\to r_{1} . \to v_{1} = \to r_{2} . \to v_{2}$
Two particles are moving with velocities $v_{1} and v_{2}$ . Their relative velocity is the maximum, when the angle between their velocities is
Azero
B $π / 4$
C $π / 2$
D $π$