Particles AandB move with constant and equal speeds in a circle as shown in (Fig. 5.164). Find the angular velocity of the particle A with respect to B, if the angular velocity of particle Aw.r.t.O is ω.
 .
.
Angular velocity of A with respect to O is
ωAO=(vAO)⊥rAO=vr=ω
Now, ωAB=(vAB)⊥rAB⇒vAB=2v
Since vAB is perpendicular to rAB⇒(vAB)⊥=vAB=2v,rAB=2r
⇒ωAB=(vAB)⊥rAB=2v2r=ω.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Subjective
40 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Single Correct
76 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.3
12 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
A particle is moving with constant speed in a circle as shown in (Fig. 5.163). Find the angular velocity of the particle A with respect to fixed point BandC if angular velocity with respect to Oisω.
 .
.
View SolutionA particle is moving in x-y plane as shown in the figure. Angular velocity of the particle with respect to the origin is
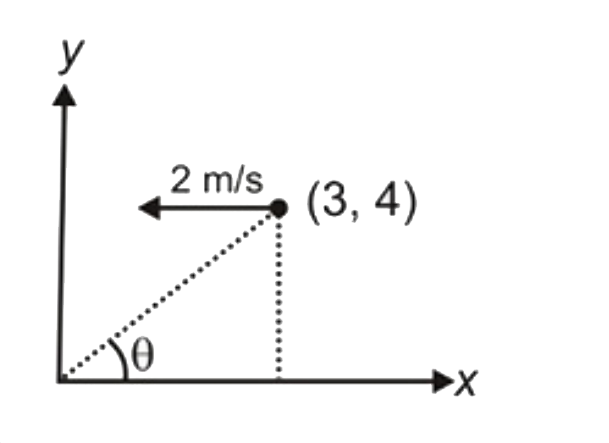
View Solution
Knowledge Check
A particle is moving with constant speed v in xy plane as shown in figure. The magnitude of its angular velocity about point O is
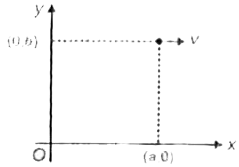 Av√a2+b2BvbCvb(a2+b2)Dva
Av√a2+b2BvbCvb(a2+b2)DvaA particle moves with constant angular velocity in a circle. During the motion its
AEnergy is conservedBMomentum is conservedCEnergy and momentum both are conservedDNone of the above is conserved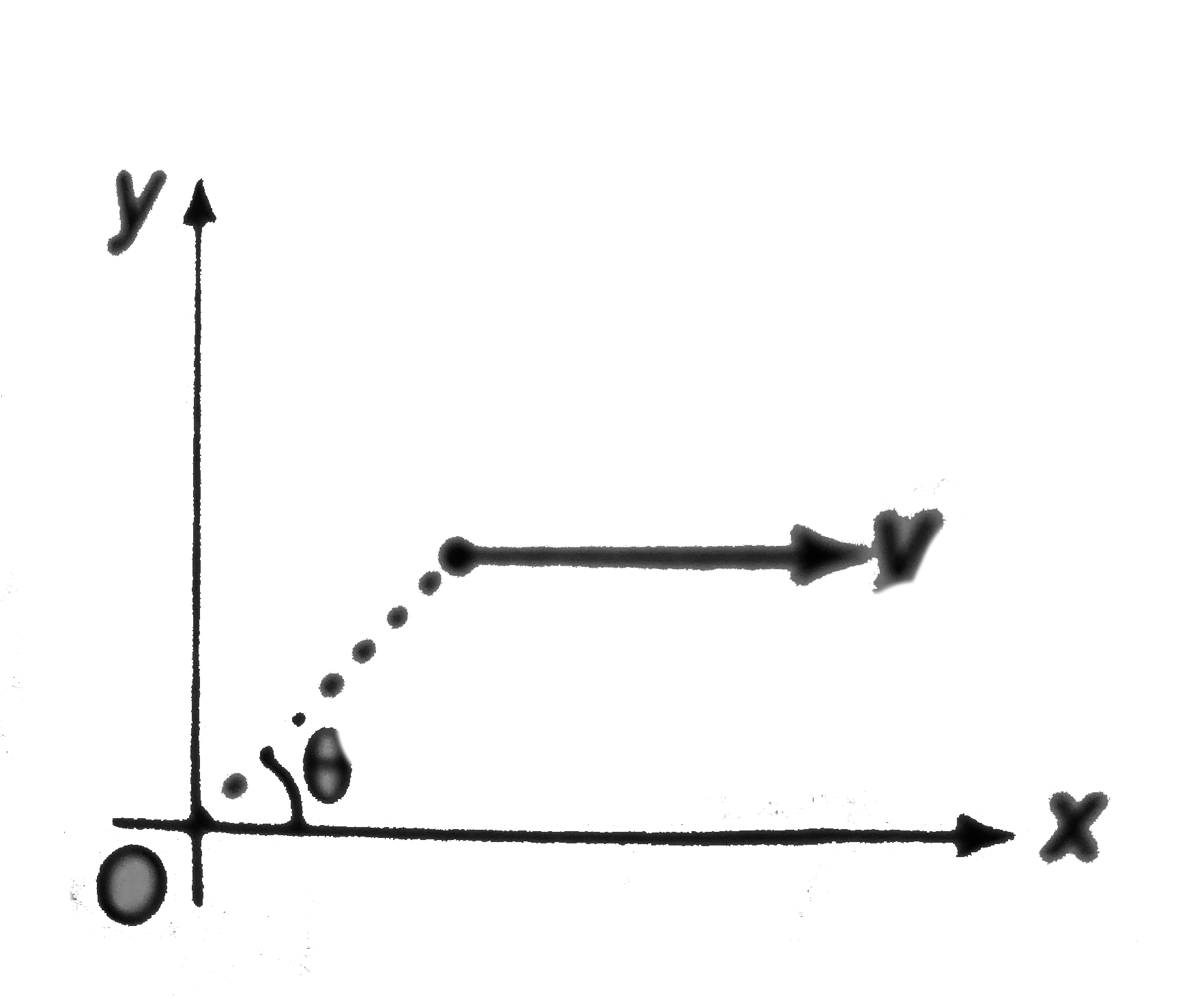
A particle mass parallel to x-axis with constant velocity v as shown in the figure. The angular velocity of the particle about the origin OAremains constantBcontinuously increasesCcontinuously decreasesDoscillates.
What is the angular acceleration of a particle moving with constant angular velocity ?
View SolutionFind the angular velocity of A with respect to O at the instant shown in (Fig. 5.165).
 .
.
View SolutionThe radius vector →r=2i+5k and the angular velocity of a particle is →w=3i−4k .Then the linear velocity of the particle is
View SolutionThe radius vector →r=2i+5k and the angular velocity of a particle is →w=3i−4k Then the linear velocity of the particle is
View SolutionA particle is moving with constant speed v along x - axis in positive direction. Find the angular velocity of the particle about the point (0, b), when position of the particle is (a, 0).
View Solution
