Question

An airplane is observed by two observers traveling at $60km{h}^{-1}$ in two vehicles moving in opposite directions on a straight road. To an observer in one vehicle, the plane appears to cross the road track at right angles while to the other appears to be ${45}^{\circ }$. At what angle does the plane actually cross the road track and what is its speed relative to ground ?

Answer

`134.16 km h^-1 ; tan^-1 2`.

Explanation

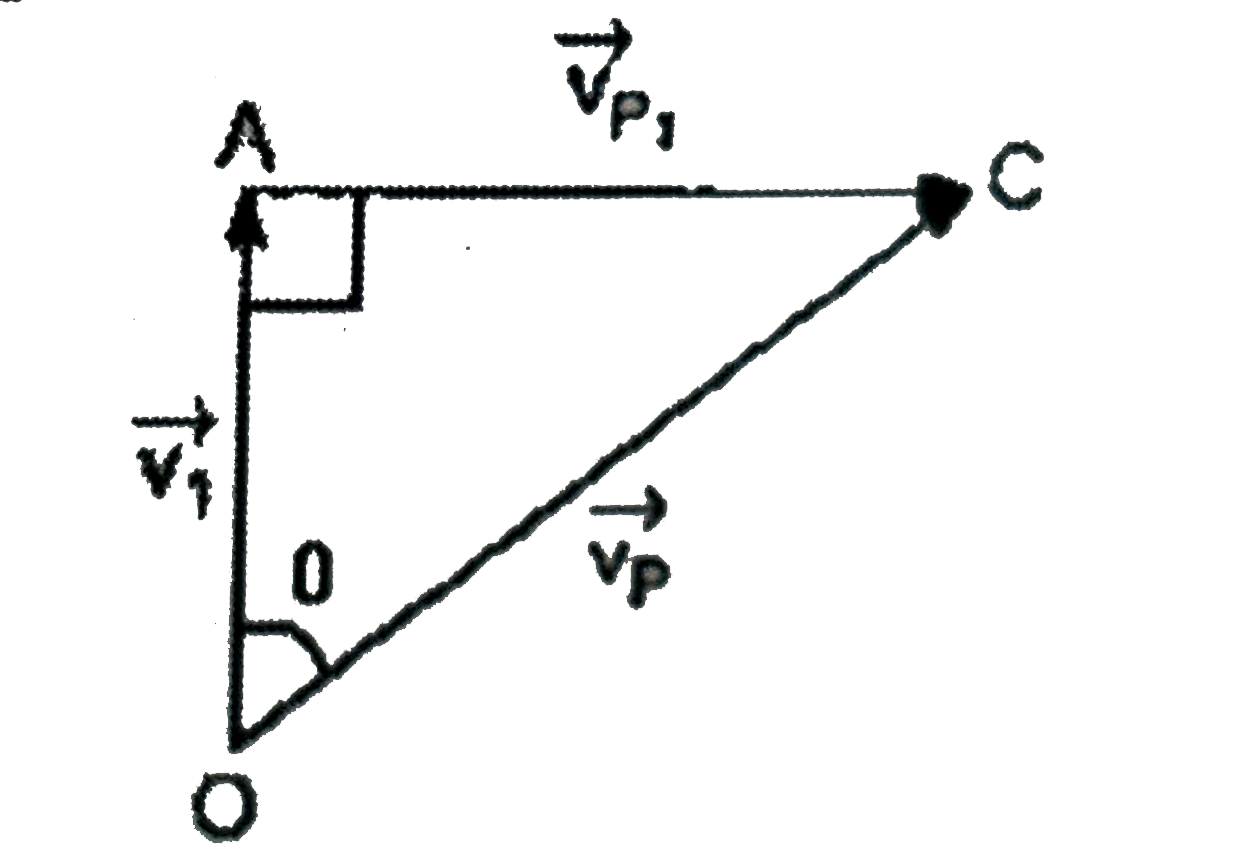
Let `v_p` be the velocity of plane relative to the ground, at angle `theta` to velocity `vec v_1` of observer in car `1`.
In case (i), `vec v_(P_1) = vec v_p - vec v_1`
`vec v_P = vec v_(P_1) + vec v_1`
Vector diagram is shown in (Fig. S5.46). Note that according to observer in car `1`, the plane crosses the road at right angles.
Similarly, in case `2 vec v_P = vec v_(p_2) + vec v_2`
We can combine (Figs S5.45) (a) and (S5.45) (b), `tan 45^@ = (AC)/(AB)`
`v_(P_1) = (v_1 + v_2) tan 45^@ = 120 xx 1 = 120 km h^-1`
`v_p = [60^2 +120]^(1//2) = 134.16 km h^-1`
`tan theta = (v_(P_1))/(v_1) = (120)/(60) = 2`
Hence, `theta = tan^-1 2`.
, .