All the particles thrown with same initial velocity would strike the ground.
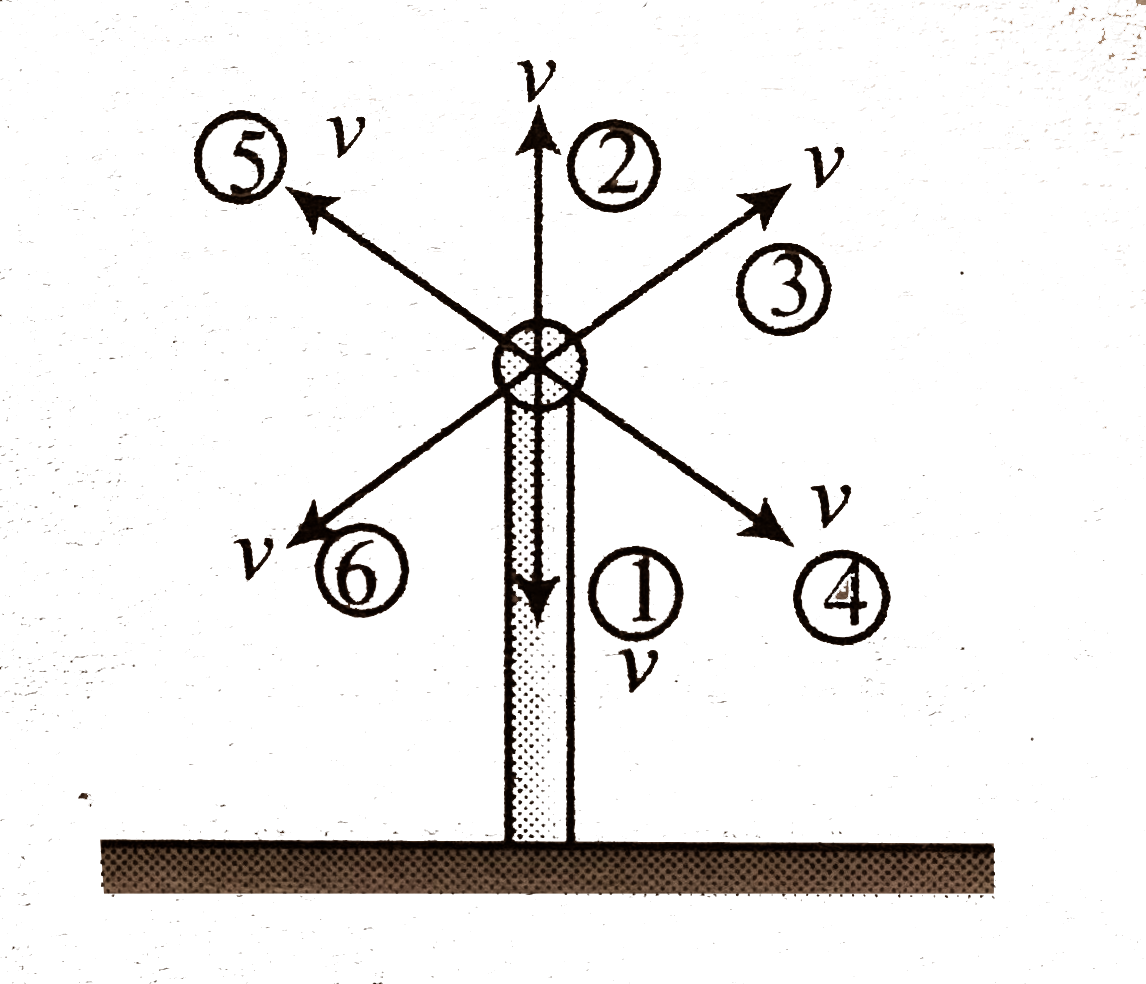 .
.
with same speed.
simultaneously
time would be least for the particle thrown with velocity v downward i.e., particle 1.
time would be maximum for the particle 2.
The correct Answer is:A, C, D
(a.,c.,d.) (KE+PE)f=(KE+PE)i in all situations.
Hence, KEf is also equal as PEf=0. Hence, all the particles collide with the same speed.
−h=vt1−12gt21 [for first particle] …(i)
−h=−vt2−12gt21 [for second particle] ...(ii)
From Eq. (i) and Eq. (ii), t2>t1
t2 = maximum, t1 = minimum
i.e., options ( c) and (d) are correct.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Assertion - Reasoning
5 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Comprehension
21 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Single Correct
76 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
A particle of mass m is released from a certain height h with zero initial velocity. It strikes the ground elastlcally (direction of its velocity is reversed but magnitude remains the same). Plot the graph between its kinetic energy and time till it returns to its initial position.
View SolutionA body is projected horizontally from the top of a tower with initial velocity 18ms−1. It hits the ground at angle 45∘. What is the vertical component of velocity when it strikes the ground ?
View Solution
Knowledge Check
A particle of mass m is connected with a string of length 2 meter. Other end of the string is fixed with a point O at a height 1 m above the ground. The particle is thrown from some point in such a way that it strikes the ground (perfectly inelastic) with velocity v0 at an angle 37∘ with vertical just below O.
 AP-2, Q-3, R-1, S-4BP-3, Q-2, R-4, S-1CP-4, Q-1, R-2, S-3DP-2, Q-3, R-4, S-1
AP-2, Q-3, R-1, S-4BP-3, Q-2, R-4, S-1CP-4, Q-1, R-2, S-3DP-2, Q-3, R-4, S-1Two bodies are thrown with the same initial velocity at angles θ and (90∘−θ) respectively with the horizontal, then their maximum height are in the ratio
A1 : 1Bsinθ:cosθCsin2θ:cos2θDcosθ:sinθA body dropped from a height h with initial velocity zero, strikes the ground with a velocity 3 m/s. Another body of same mass is thrown from the same height h with an initial velocity of 4 m/s. Find the final velocity of second mass, with which it strikes the ground.
A5 m/sB12 m/sC3 m/sD4 m/s
A particle is thrown with velocity u at an angle ∝ from the horizontal. Another particle is thrown with the same velocity at an angle ∝ from the verticle. What will be the ratio of times of flight of two particles ?
View SolutionA particle is thrown vertically upward from the ground with some velocity and it strikes the ground again in time 2 s. The maximum height achieved by the particle is : (g=10m/s2)
View SolutionAssertion: In projectile motion horizontal velocity remains same but vertical velocity continously change and particle strikes the ground with same vertical velocity with which the particle was thrwon in vertical direction.
View SolutionA stone is thrown upwards from the top of a tower with some initial speed and it reaches the ground in 16 seconds. Now it is thrown with the same initial speed downward and it reaches the ground in 9sec. In how much time will it reach the ground if the stone is allowed to fall freely under gravity from the same place ?
View SolutionAn object is thrown vertically upward with a certain initial velocity in a world where the acceleration due to gravity is 19.6m/s2. The height to which it rises is _____ that to which the object would rise if thrown upward with the same initial velocity on the Earth. Neglect air resistance.
View Solution
