A ball is thrown from a point in level with velocity u and at a horizontal distance r from the top os a tower of height h.
How must the speed and angle of the projection of the ball be related to r in order that the ball may just go grazing the top edge of the tower ?

gr=u2sin2θ
gr=u2sinθ
gr=u2cos2θ
gr=u2cosθ
The correct Answer is:C
( c) Here r will become range
r=u2sin2θg
⇒gr=u2sin2θ
h=usinθt+12gt2
x=ucosθt
t=xucosθ
h=usinθxucosθ+12g(x2)u2cos2θ
gx2+2u2sinθcosθx−2hu2cos2θ=0
x=ucosθg[√u2sin2θ+2gh−usinθ].
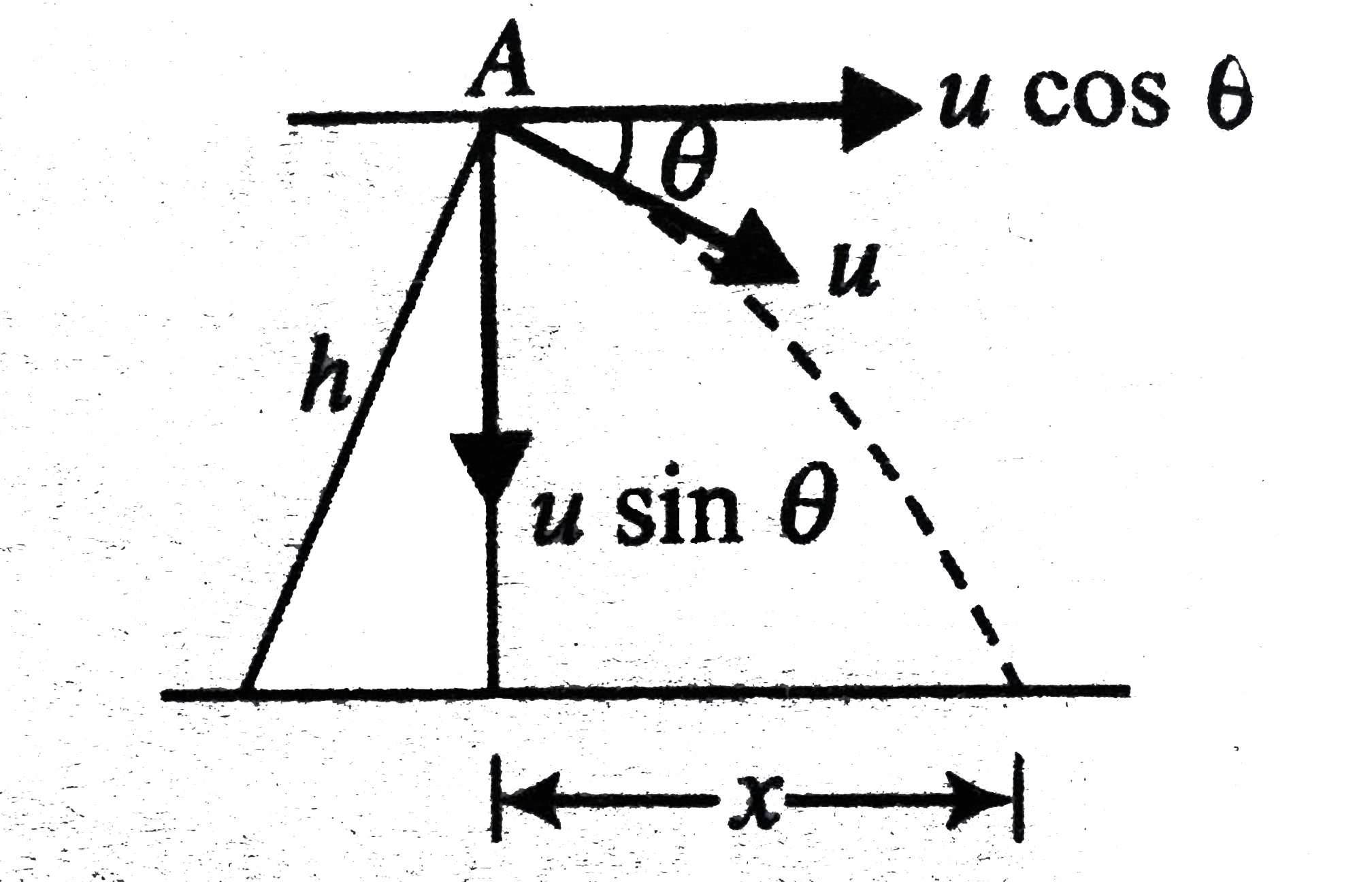 .
.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer9videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Assertion - Reasoning5videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
Similar Questions
A ball is thrown with velocity 40m/s at angle 30∘ with horizontal from the top of a tower of height 60m. At what horizontal distance from the foot of tower, the ball will strike the gorund ?
View SolutionIf the distance of a point from the tower is equal to the height of the tower , then find the angle of elevation of the top of the tower from that point .
View Solution
Knowledge Check
- Question 1 - Select One
A ball is thrown from a point in level with velocity u and at a horizontal distance r from the top of a tower of height h.
At what horizontal distance x from the foot of the tower does the ball hit the ground ? Aucosθg{(u2sin2θ+gh)1/2−usinθ}Bucosθg{(u2cos2θ+2gh)1/2−ucosθ}Cucosθg{(u2cos2θ+gh)1/2−ucosθ}Ducosθg{(u2cos2θ+gh)1/2−ucosθ}
Aucosθg{(u2sin2θ+gh)1/2−usinθ}Bucosθg{(u2cos2θ+2gh)1/2−ucosθ}Cucosθg{(u2cos2θ+gh)1/2−ucosθ}Ducosθg{(u2cos2θ+gh)1/2−ucosθ} - Question 2 - Select One
A ball is released from the top of a tower of height h metre. It takes T second to reach the ground. What is the position of the ball in T/3 sccond?
Ah/9 metre from the groundB7h/9 metre from the groundC8h/9 metre from the groundD17h/18 metre from the ground. - Question 3 - Select One
A ball is thrown with speed 40m/s at an angle 30∘ with horizontally from the top of a tower of height 60m. Choose the correct option
Athe vertical component of velocity first decreases to zero and then increasesBthe ball reaches the ground after 6sCif the ball strikes the ground at maximum horizontal distance from the tower for this the angle of projection should be less than 45∘Dall option are correct
From the top of a pole of height h, the angle of elevation of the top of the tower is α. The pole subtends an angle β at the top of the tower. The height of the tower is____
View SolutionA stone is thrown horizontally with a velocity 2√gh from the top of a tower of height h. It strikes the ground level through the foot of tower at a distance x from it. What is the value of x?
View SolutionA ball is released from the top of a tower to height h. It takes T seconds to reach the ground. What is the position of ball in T/3 seconds?
View SolutionA ball is released from the top of a tower of height h metre. It takes T second to reach the ground. What is the position of the ball in T3 second?
View Solutiona body is thrown horizontally with a velocity √2gh from the top of a tower of height h. It strikes the level gound through the foot of the tower at a distance x from the tower. The value of x is :-
View Solution

