A homogeneous flexible rope rests on a wedge whose side edges make angles α and β with the horizontal. The central part of the rope lies on the upper rib C of the wedge. With what acceleration should the wedge be pulled to the left along the horizontal plane in order to prevent the displacement of the rope with respect to the wedge? [Consider all surfaces to be smooth]
![A homogeneous flexible rope rests on a wedge whose side edges make angles alpha and beta with the horizontal. The central part of the rope lies on the upper rib C of the wedge. With what acceleration should the wedge be pulled to the left along the horizontal plane in order to prevent the displacement of the rope with respect to the wedge? [Consider all surfaces to be smooth]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_V01_C06_S01_020_Q01.png)
Consider the parts of rope on either size of incline as two different elements. Draw FBD. Apply Newton's law on these parts separately
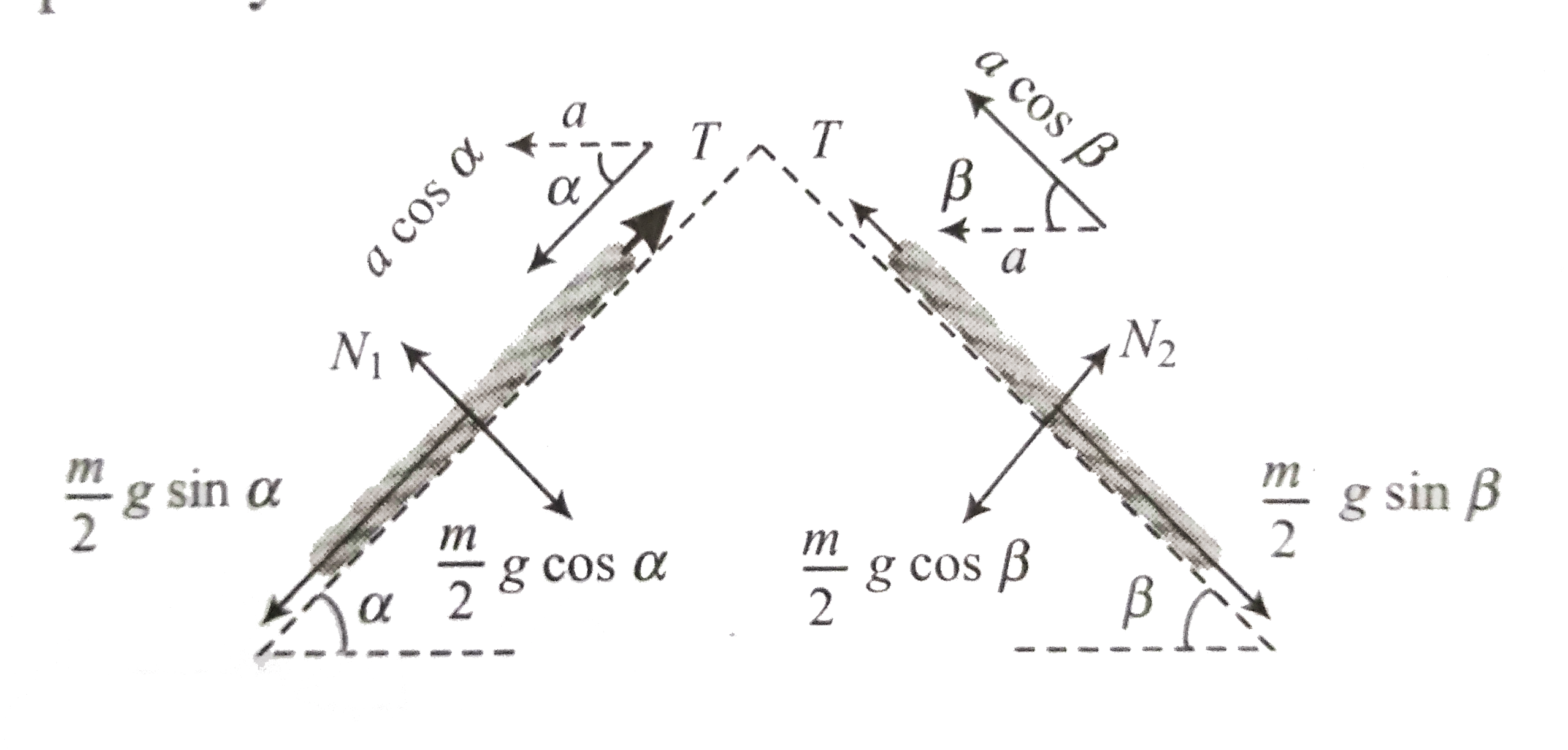
Taking components of acceleration along incline surface,
For left side part of rope: mg2sinα−T=m2acosα
For right side part of rope: T−mg2sinβ=m2acosβ
On solving, we get a=g[sinα−sinβ]cosβ+cosα.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples11videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.111videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
A homogeneous and flexible chain rests on a wedge whose side edges make-angle α and β with the horizontal [refer Fig. 2E., 10(a)]. The cehtrarparcuf the chain lies on the upper tip of the wedge. With what acceleration should the wedge be pulled to the left along the horizontal plane in order to prevent the, displacement of the chain with respect to the wedge?
[Consider all surfaces to be smooth]
View SolutionA wedge of mass M rests with one face in contact with horizontal , smooth surface . A particle of mass m is placed on the smooth face on it , inclined at an angle αto the horizontal and released . Find the velocity of the wedge and that of the particle relative to the wedge when the particle has slipped a distance x down the face of the wedge . Also calculate the acceleration of the wedge and that of the particle relative to the wedge and the smooth surface .
[Hint : Apply principal of conservation of momentum along the horizontal and energy conservation principle . See Example 8 )View Solution
Knowledge Check
- Question 1 - Select One
A small block of mass m rests on a smooth wedge of angle θ. With what horizontal accelaration a should the wedge be pulled, as shown in fig, so that the block falls freely?
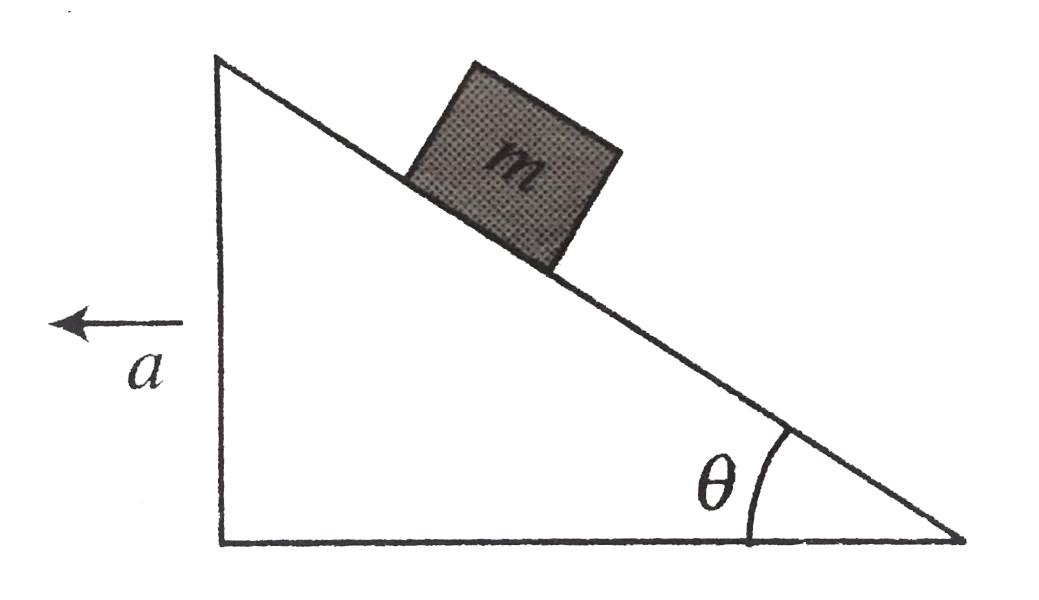AgcosθBgsinθCgcotθDgtanθ - Question 2 - Select One
In the figure heavy mass m moves down the smooth surface of a wedge making an angle α with the horizontal. The wedge at rest t=0 is on a smooth surface. The mass of the wedge is M the direaction of motion of the mass m makes an angle β with the horizontal then, Tanβ is
.AmMtanαBMmtanαC(1+mM)tanαD(1+Mm)tanα - Question 3 - Select One
A weightless inextensible rope rests on a stationary wedge forming an angle α with a horizontal One end of the rope is fixed to the wall to point A.A small load is attached to the rope at point B The wedge starts moving to the right with a constant acceleration a The acceleration of the load is given by
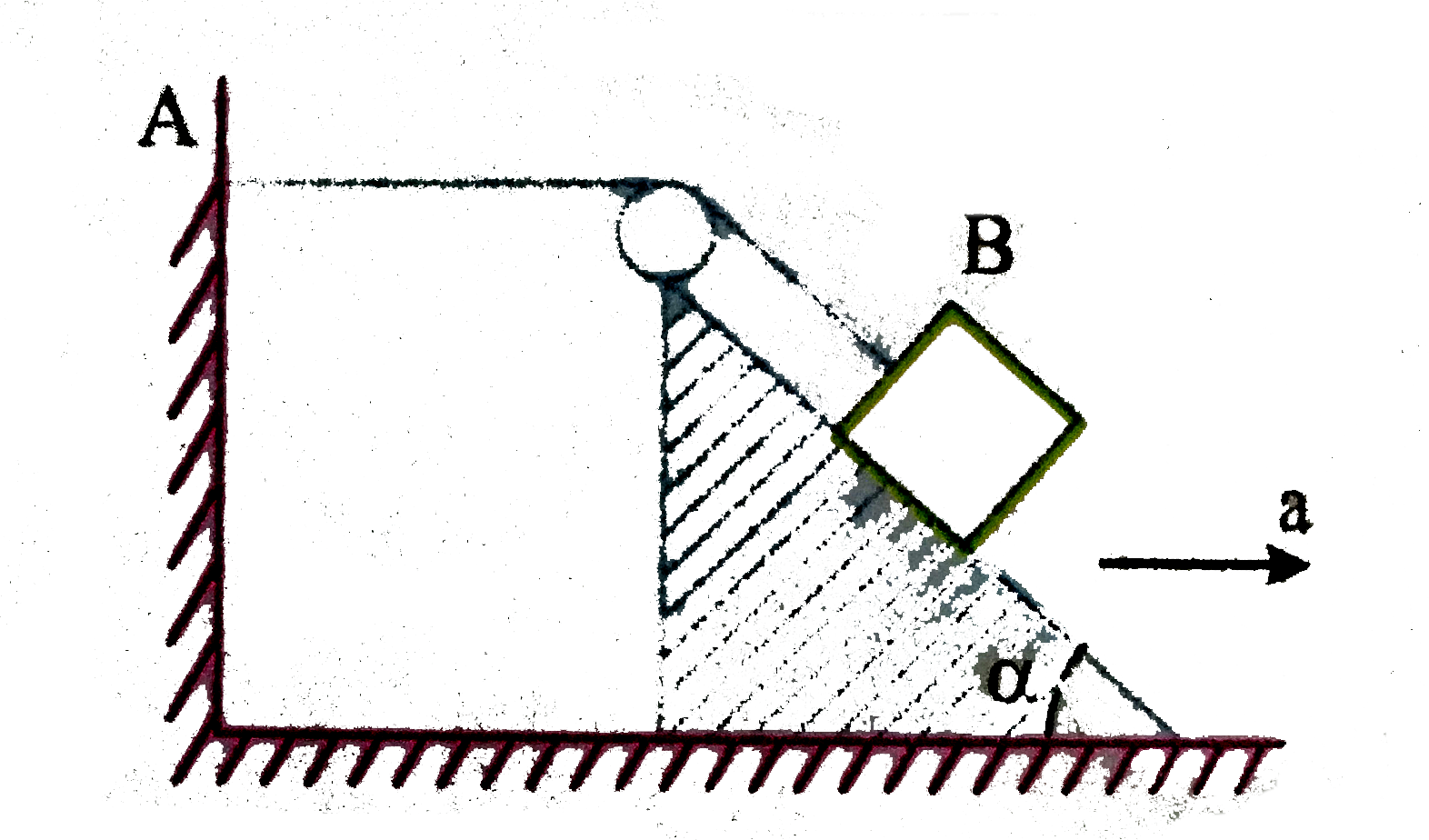.AaB2asin(.α/2)CasinαDsin(.α/2)
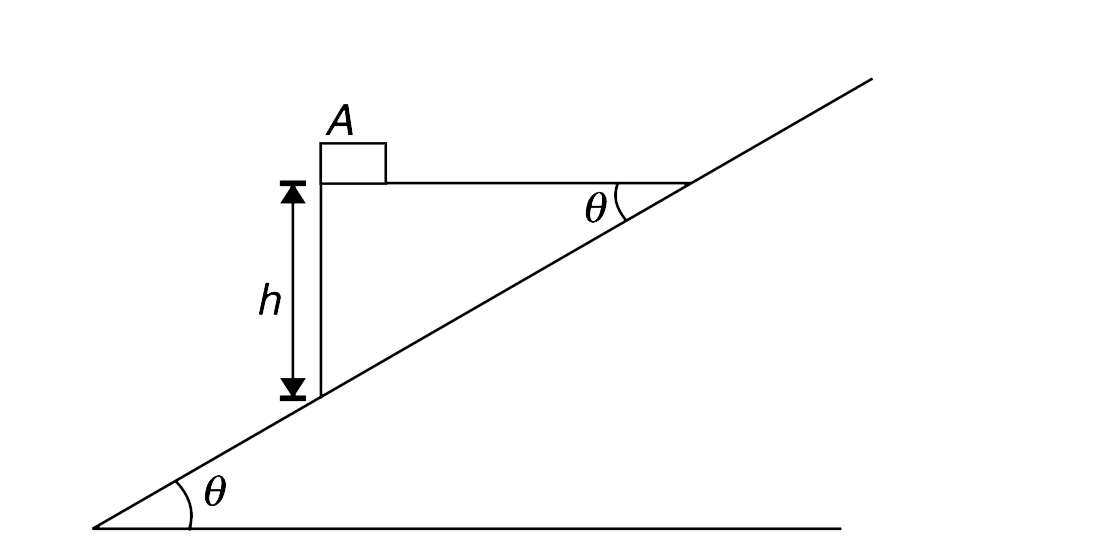
A wedge is placed on the smooth surface of a fixed incline having inclination θ with the horizontal. The vertical wall of the wedge has height h and there is a small block A on the edge of the horizontal surface of the wedge. Mass of the wedge and the small block are M and m respectively.
(a) Find the acceleration of the wedge if friction between block A and the wedge is large enough to prevent slipping between the two.
(b) Find friction force between the block and the wedge in the above case. Also find the normal force between the two.
(c) Assuming there is no friction between the block and the wedge, calculate the time in which the block will hit the incline.
View Solution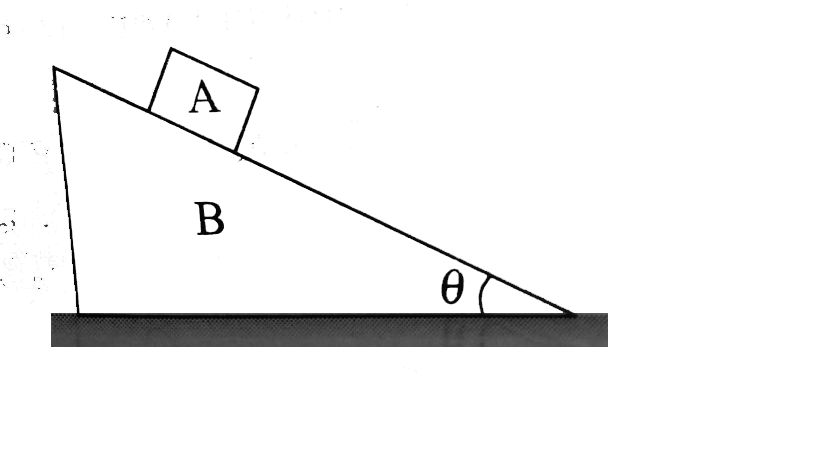
A block is placed on a smooth wedge of inclination angle θ with the horizontal. What minimum acceleration should be given to the wedge in the horizontal direction so that the block starts moving up along the incline?View SolutionA block of mass m is placed on an inclined plane. With what acceleration A towards right should the system move on a horizontal surface so that m does not slide on the surface of inclined plane? Also calculate the force supplied by wedge on the block. Assume all surfaces are smooth.
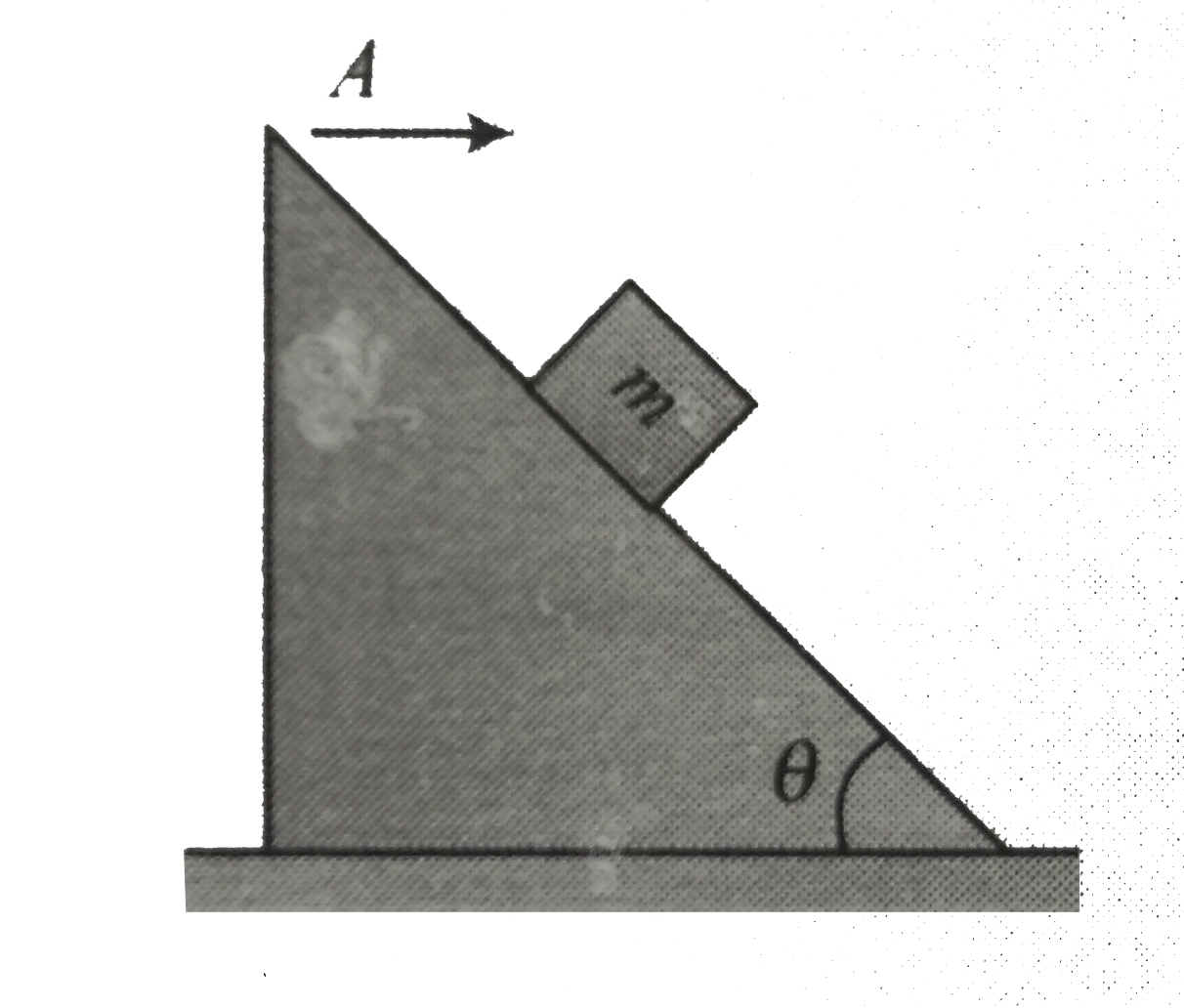View SolutionA uniform of rope length L and mass M is placed on a smooth fixed wedge as shown. Both ends of rope are at same horizontal level. The rope is initially released from rest, then the magnitude of initial acceleration of rope is.
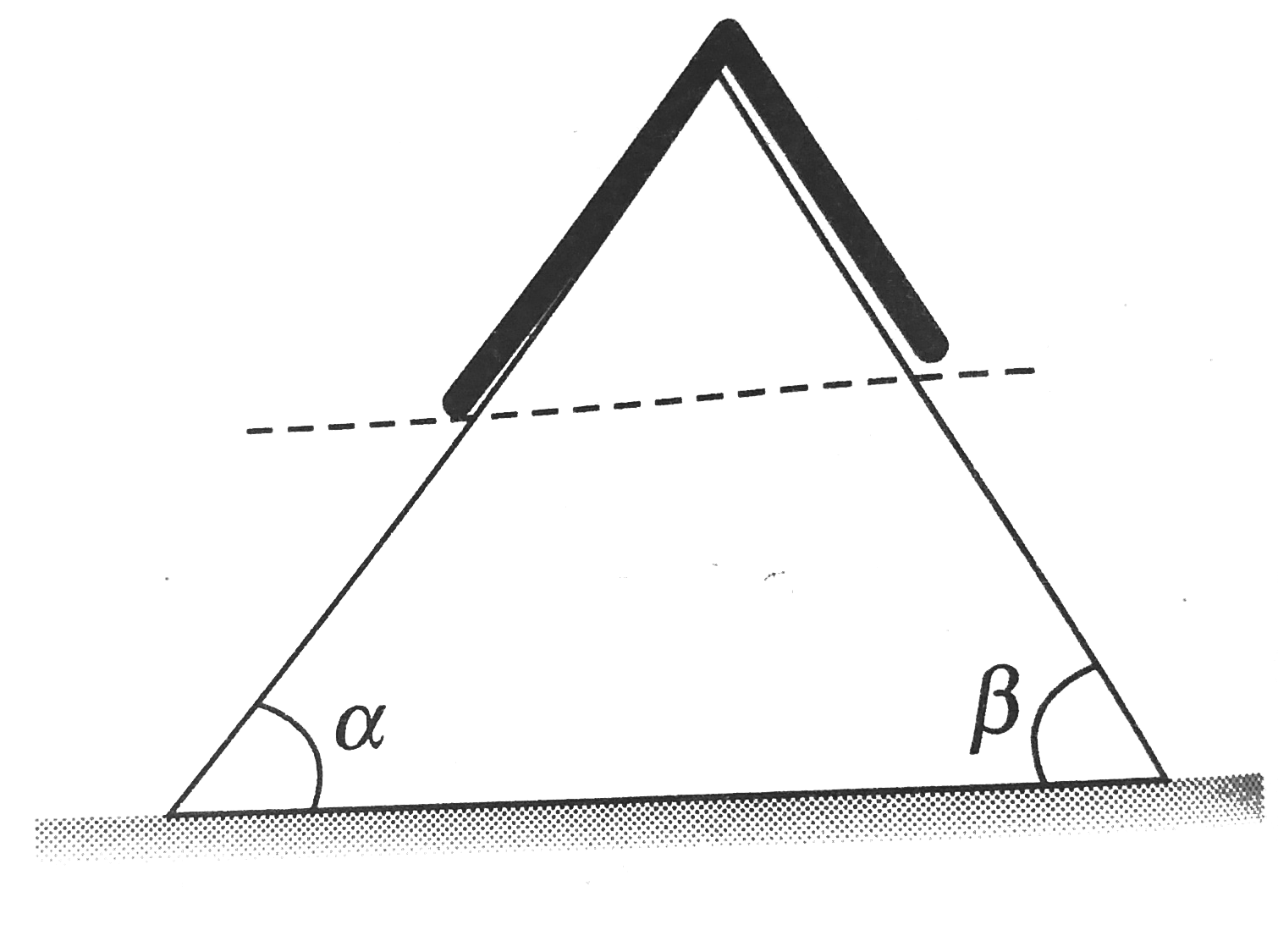View SolutionA small block m is placed at the top on the smooth inclined face AB of a wedge of mass M free to slide on a horizontal surface as shown in the figure and released from rest.
(i) The total momentum of the block and the wedge is constant during motion.
(ii) The total momentum of the block and the wedge along the horizontal is constant during motion.
(iii) When the block reaches B the displacement of M to the left is mhcotαm+M.
(iv) When the block reaches B the horizontal displacement of m to the right is Mhcotαm+M.View Solution