In fig. a ball of mass m1 and a block of mass m2 are joined together with an inextensible string. The ball can slide on a smooth horizontal surface. If v1 and v2 are the respective speeds of the ball and the block, then determine the constraint relation between the two.
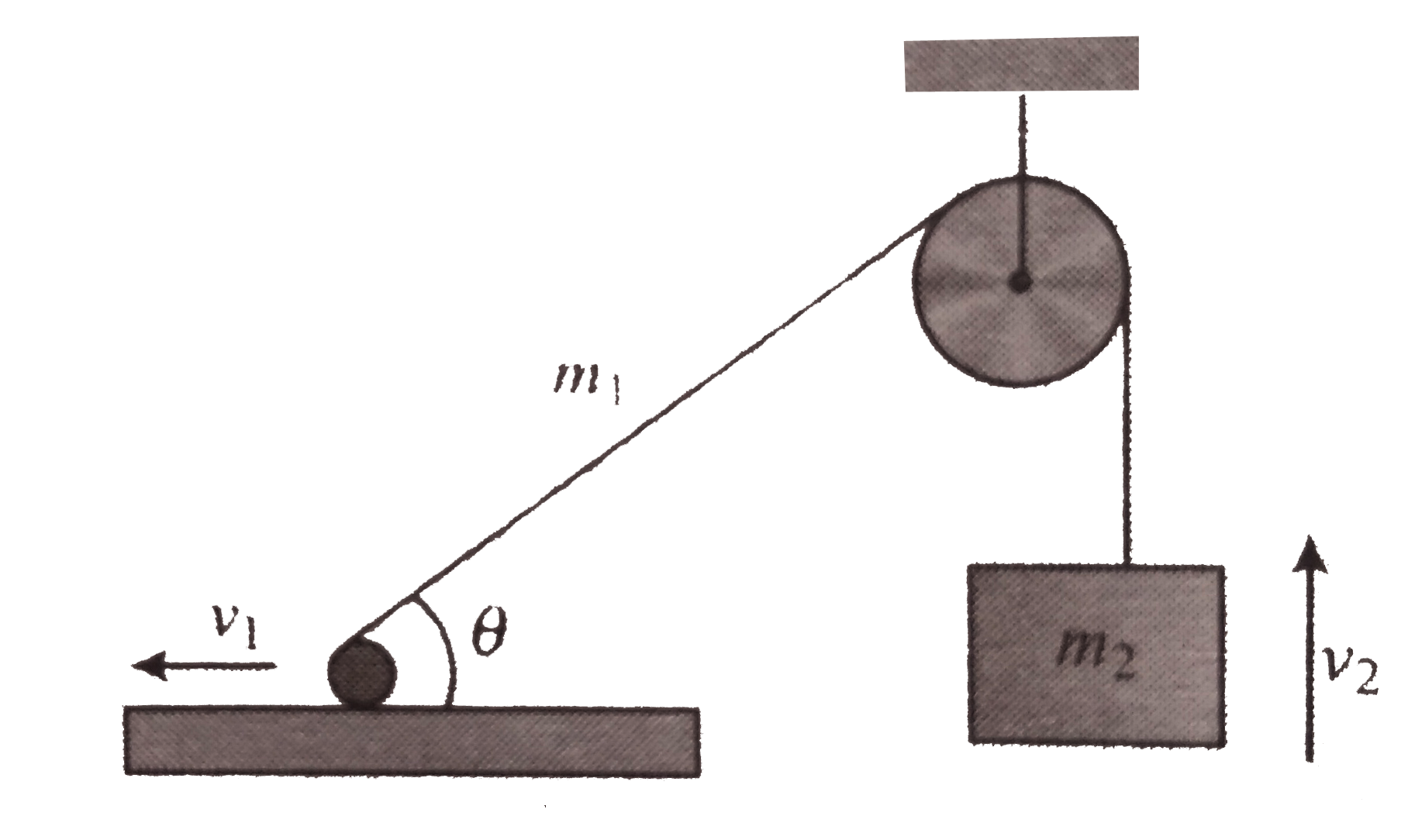
Method 1: Distances are assumed from the center of the pulley as shown in fig.
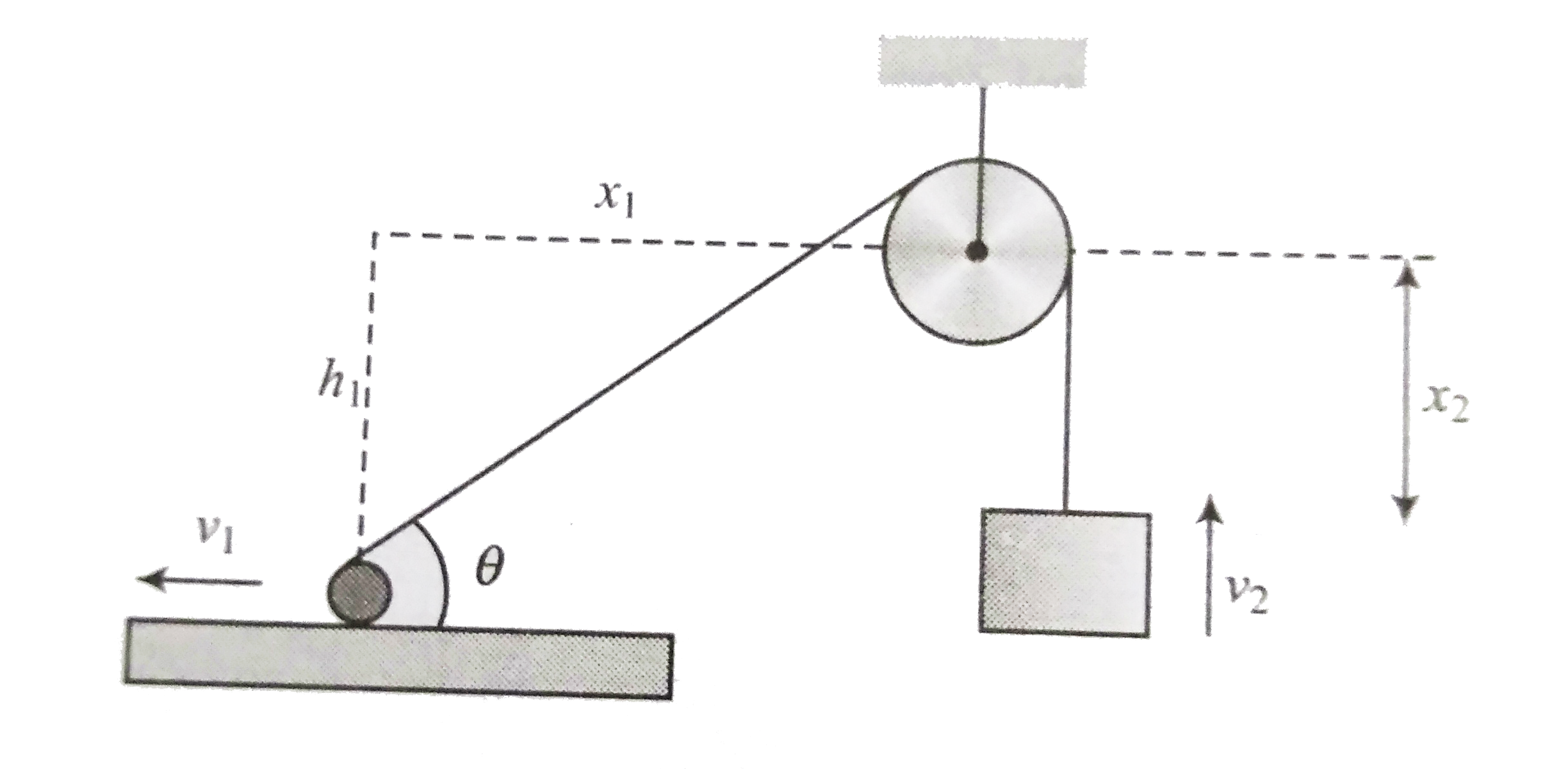
Consraint: Length of the string remains constant.
√x21+h21+x2 = constant
Differentiating both the side w.r.t. time, we get
2x12√x21+h21dx1dt+dx2dt=0
Since the ball moves so as to increases x1 with time and block moves so as to decrease x2 with time,
dx1dt+v1 and dx2dt=−v2
also, x1√x21+h21=cosθ or v2=v1cosθ
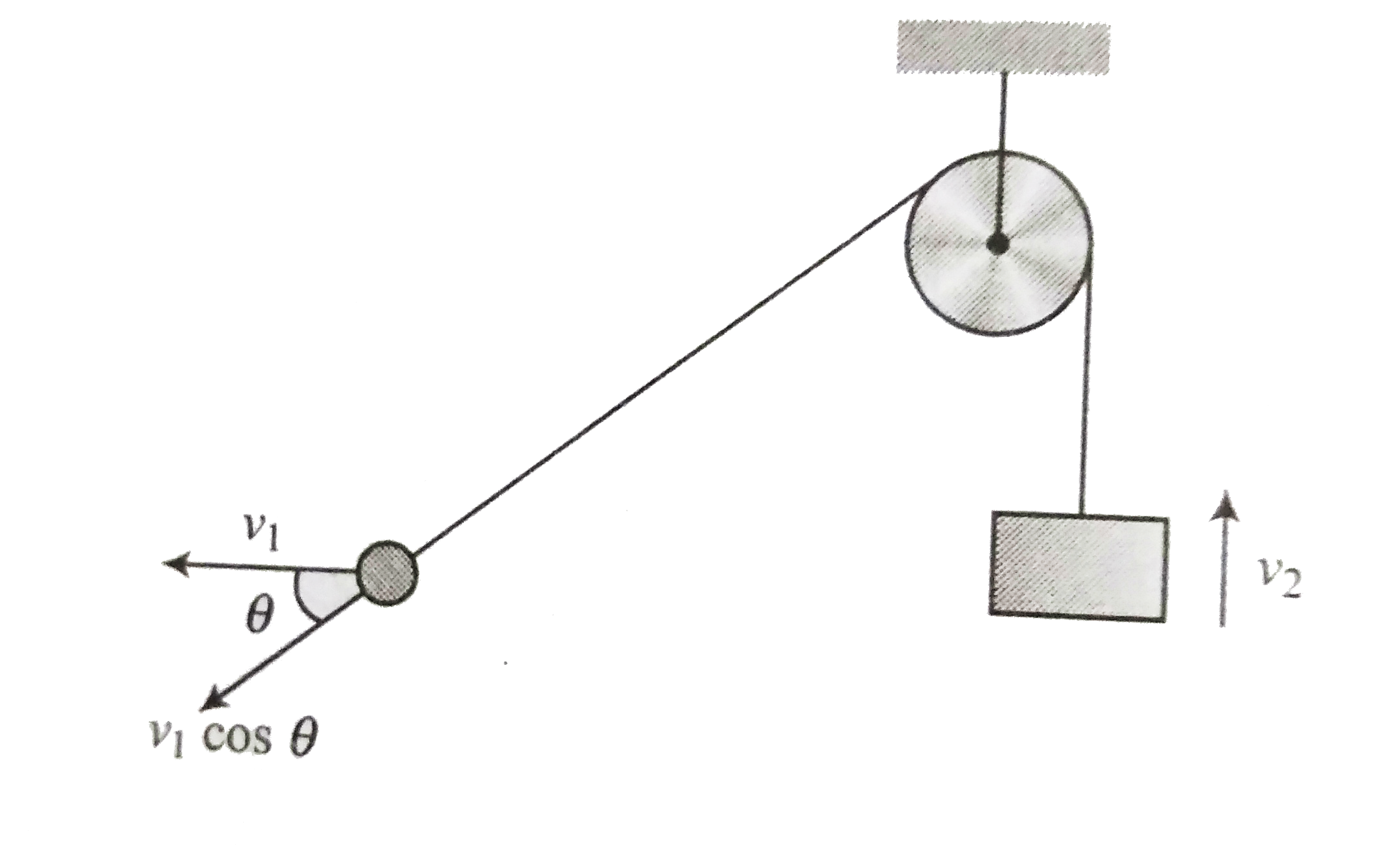
Method 2: The problem can be solved very easily if we look at the problem from a different viewpoint and identify a difference constraint. i.e., the velocity of any two points along the string is same. Obviously, from fig., we have v1cosθ=v2
Method 3: Change in length of segment I,
Δl1=0±(x2)=−x2

Change in length of segment II,
Δl1=(x2cosθ)+0=x1cosθ
Total change in the length of all segments should be zero, as the length of string is constant.
Δl=Δl1+Δl2
=−x2+x1cosθ=0
⇒x2=x1cosθ or v2=v1cosθ.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.1
11 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Video
Similar Questions
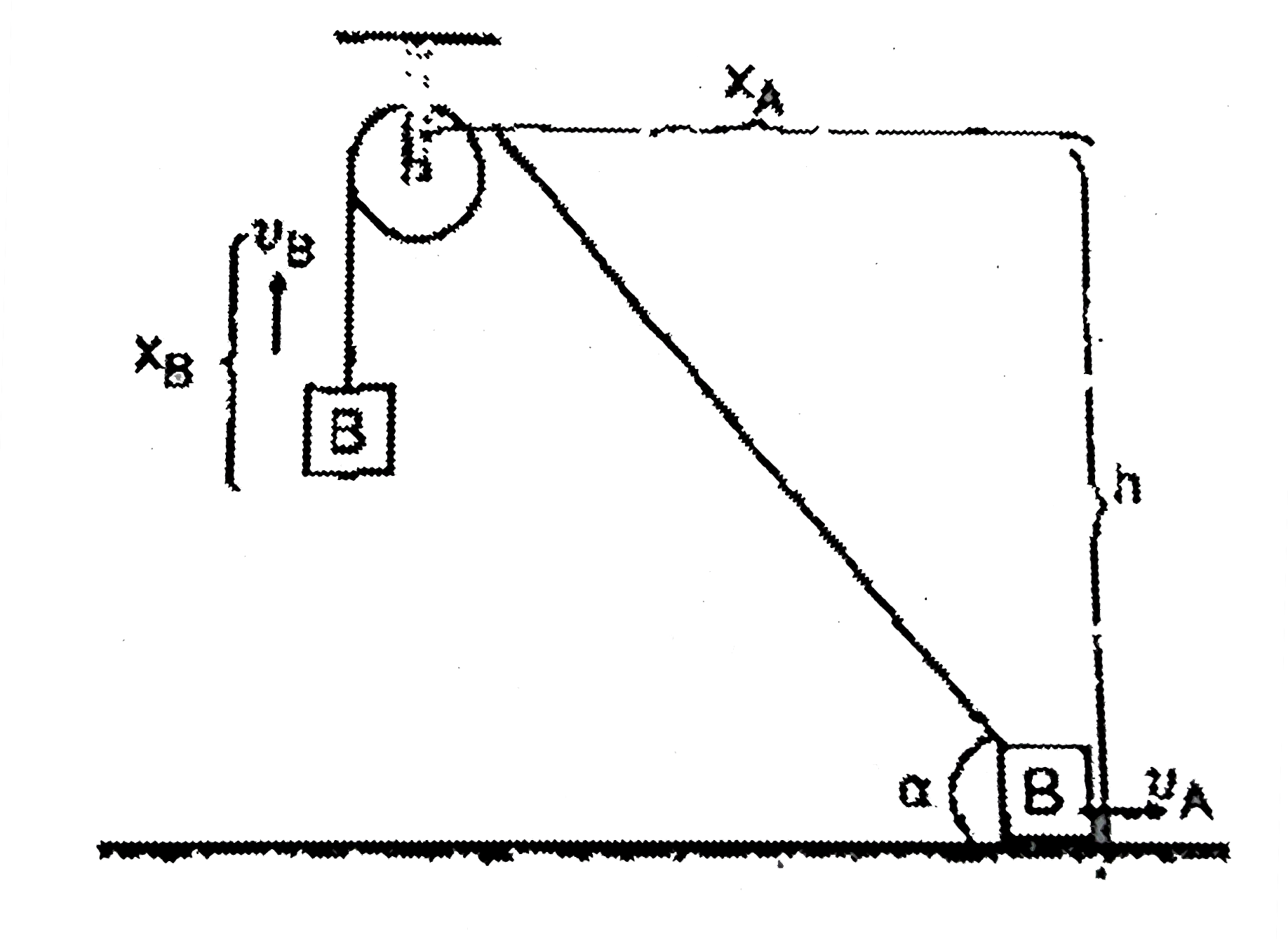
In the Fig. the blocks 'A' and 'B' are connected with an inextensible string. The block 'A' can slide on a smooth horizontal surface.
View SolutionTwo blocks of masses m and M are connected by an inextensible light string . When a constant horizontal force acts on the block of mass M. The tension in the string is
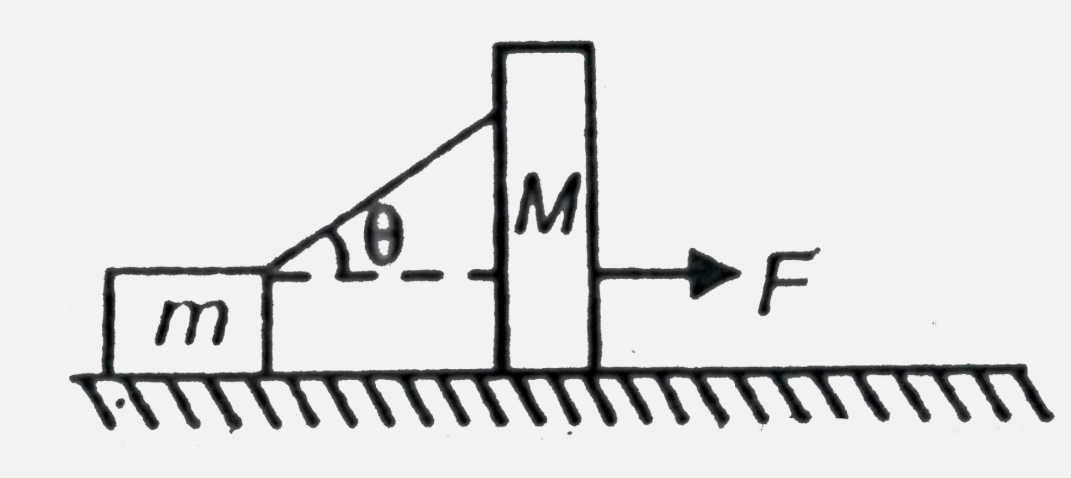
View Solution
Knowledge Check
A ball of mass m1 and another ball of mass m2 are dropped from equal height. If the time taken by the balls are t1 and t2, respectively, then
At1=t2Bt1=2t2Ct1t2=m1m2Dt1t2=m2m1Two identical small balls, each of mass m, are connected by a massless and inextensible string of length l and placed on a smooth horizontal xy plane. An external agent pulling the string from its mid-point along y-axis with velocity v0 as shown in Fig. When the separation between the two balls reduces to l/2 then the speed of each ball will be
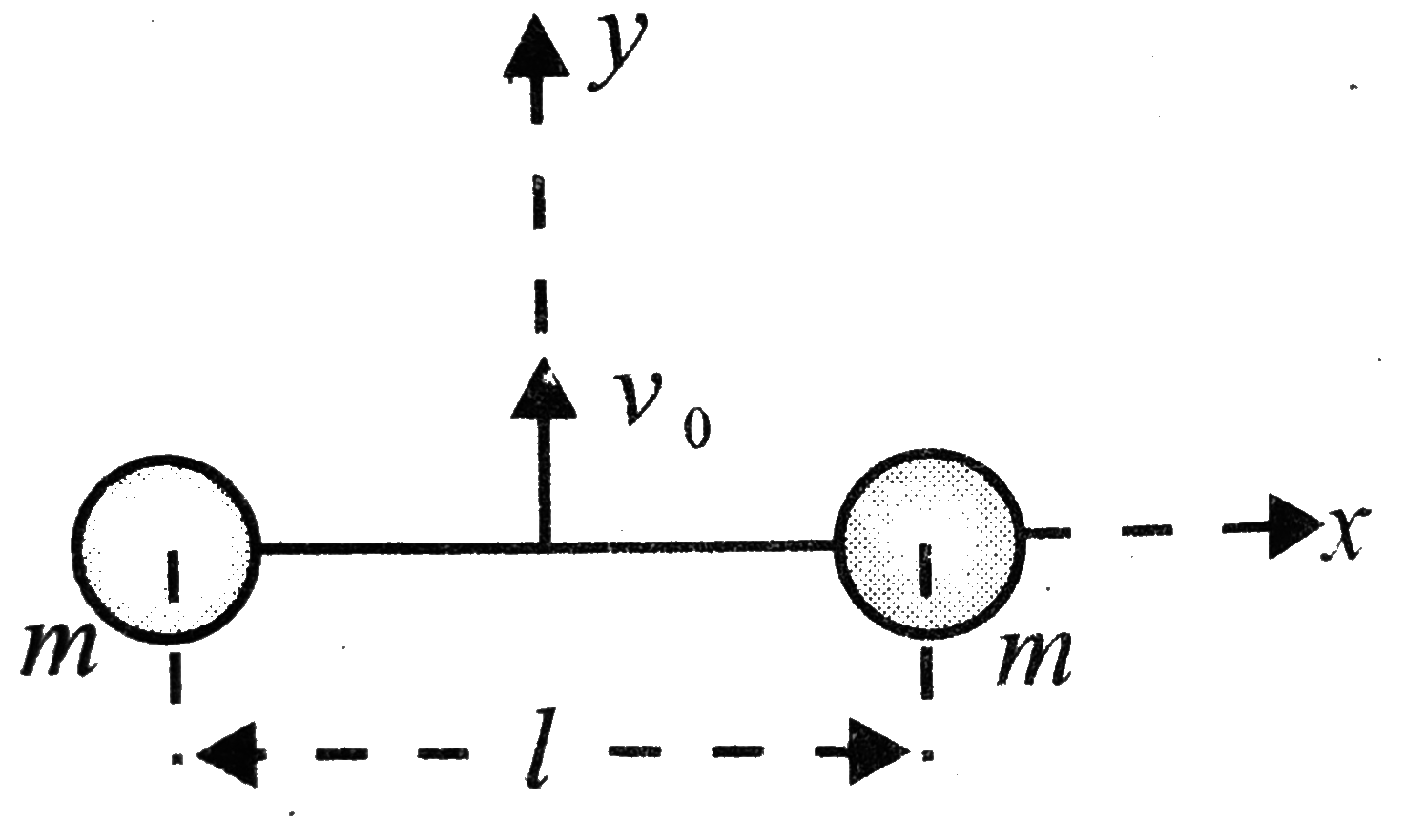 A2v0Bv0Cv02Dnone of the above
A2v0Bv0Cv02Dnone of the aboveA ball of mass m1, collides elastically and head on with ball of mass m2 at rest. Then
AThe transfer of kinetic energy to the second ball is maximum when m1=m2BThe change of momentum of first ball is maximum, when m1<<m2.CThe velocity of the second ball is maximum, when m1>>m2.DNone of these
Two block of masses m1andm2 are placed side by side on a smooth horizontal surface as shown in fig. A horizontal force F is applied on the block .

(a) Find the acceleration of each block.
(b) Find the normal reaction between the two blocks.
View SolutionTwo identical balls each of mass m interconnected by a small light inextensible string are kept on a smooth horizontal surface. One of the balls is pushed towards the other with a speed v0 find the loss of K.E. of the ball. What will be the final velocities of the balls ? (e=1).

View SolutionTwo blocks of mass m1andm2 are connected by light inextensible string passing over a smooth fixed pulleuy of negligible mass. The acceleration of the centre of mass of the system when blocks move under gravity is :
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.

What is acceleration of centre of mass of system at the instant of maximum elongation of spring
View SolutionThere blocks of masses m1 , m2 and m3 are connected by may less unstretchable strings on a smooth surface. Tension T2 is.
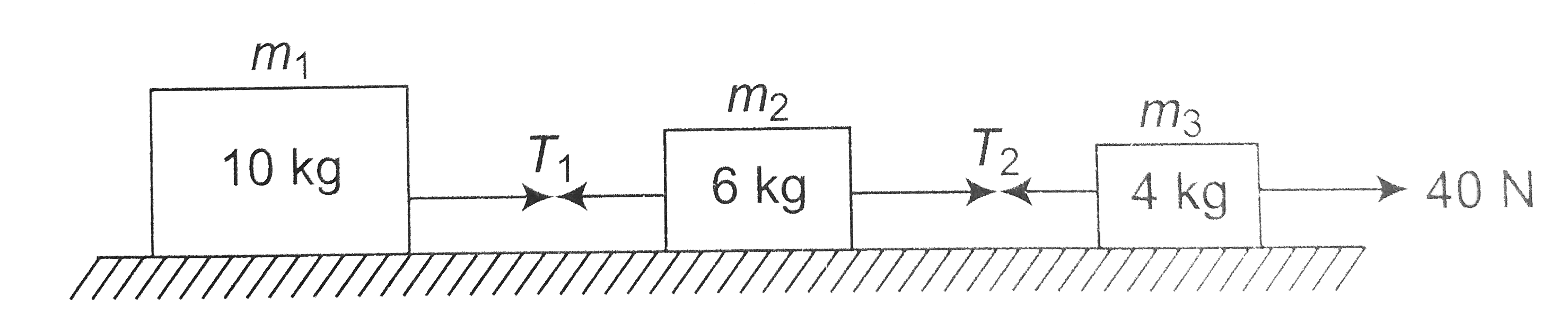
View Solution