In figure find the acceleration of m assuming that there is friction between mandM and all other surface are smooth and pulleys light and μ=coefficient of friction between mandM

The correct Answer is:2√5mgm+5m+2μm
Let X be the leftward displacement of M and xandy be the leftward and downward displacement of m as shown in the fig Then by constant relationwe have
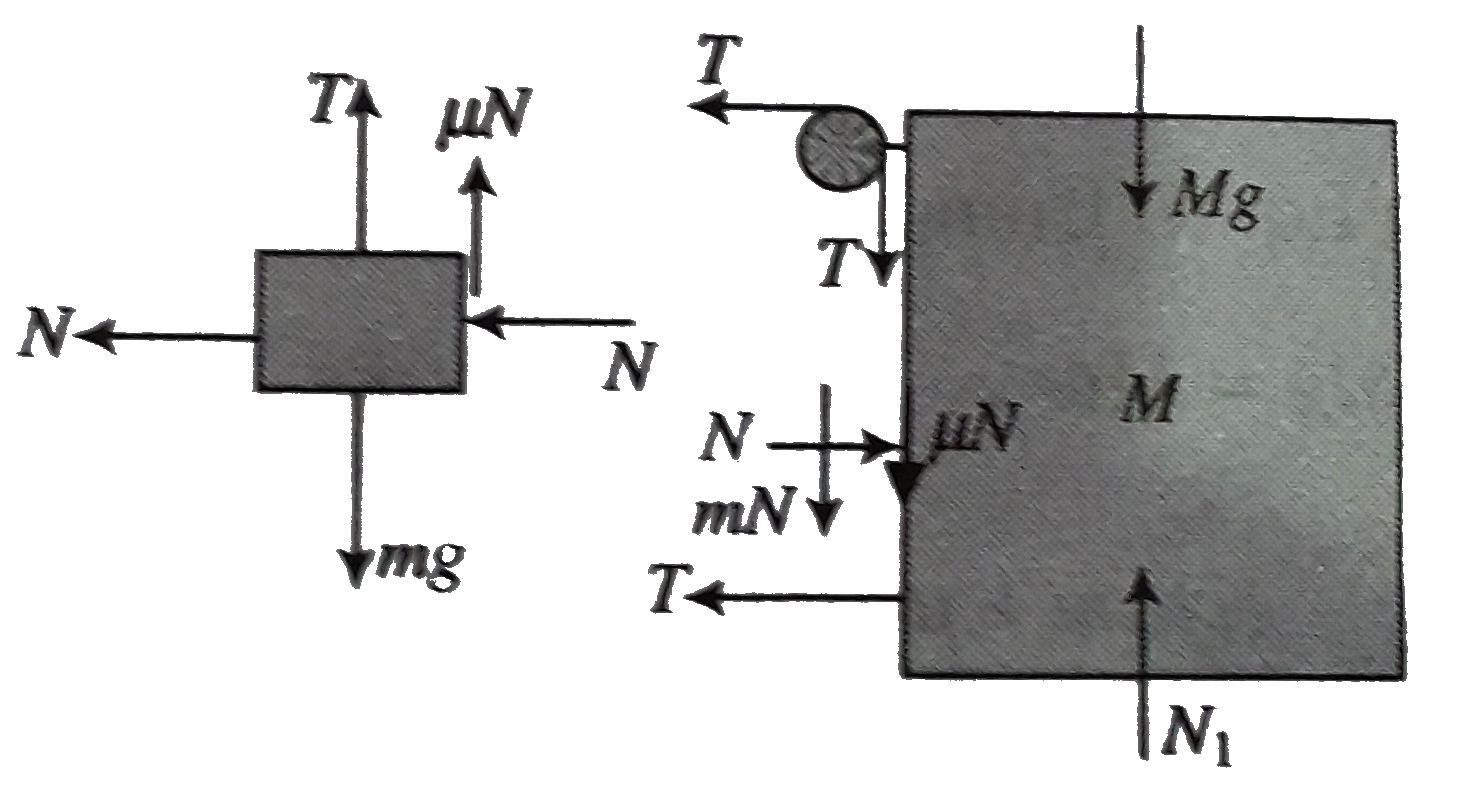
x=X⇒..x=..X⇒ax=Ax
and l1−x+l2+3−x+l4+y=l1+l2+l3+l4
wherel1,l2,l3,l4are the instantaneous length of the segments of the string
⇒2x=y⇒2..x=..y⇒2ax=ay
N=max and mg−μN−T=may and 2T−N=MAx=Max
Eliminating T,A and N
ax=2mgM+5m+2μm and 4mgM+5m+2μm
∴a=√a2x+a2y=2√5mgm+5m+2μm
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Single Correct
87 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct
2 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.3
27 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
In figure find the acceleration of m assuming that there is friction between mandM and all other surfaces are smooth and pulleys light and μ=coefficient of friction between mandM

View SolutionIn figure , find the acceleration of m assuming that there is friction between m and M,and all other surface are smooth and pulleys light and m = coeffiicient of friction between m and M .
View Solution
Knowledge Check
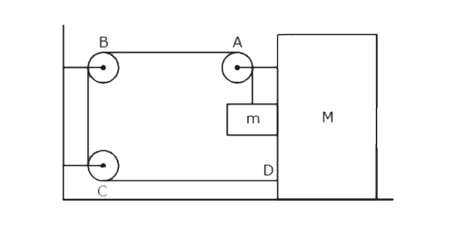
In the figure shown a ring of mass M and a block of mass m are in equilibrium. The string is light and pulley P does not offer any friction and coefficient of friction between pole and M is μ. The frictional force offered by the pole to M is
 AMg directed upBμ mg directed upC(M-m) g directed downDμ mg directed down
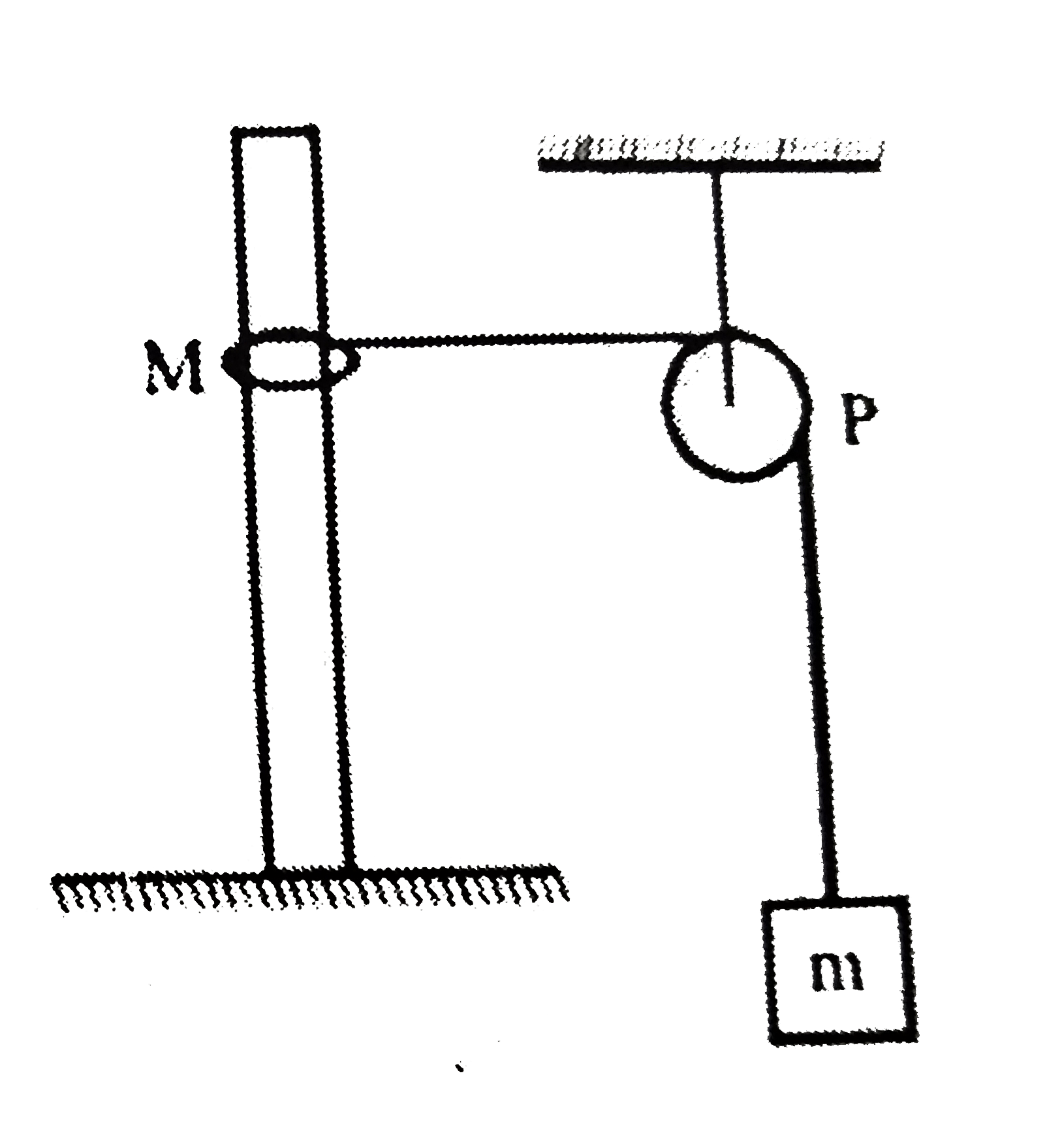
AMg directed upBμ mg directed upC(M-m) g directed downDμ mg directed downWith what minimum acceleration mass M must be moved on frictionless surface so that m remains stick to it as shown in figure-2.171. The co-efficient of friction between M & m is μ :
 AμgBgμCμmgM+mDμmgM
AμgBgμCμmgM+mDμmgMIn the arrangement shown in Fig there is no friction between of mass 2m and ground but there is friction between the block of masses m is stationary with respect to block of mass 2m The value of friction between m and 2mis
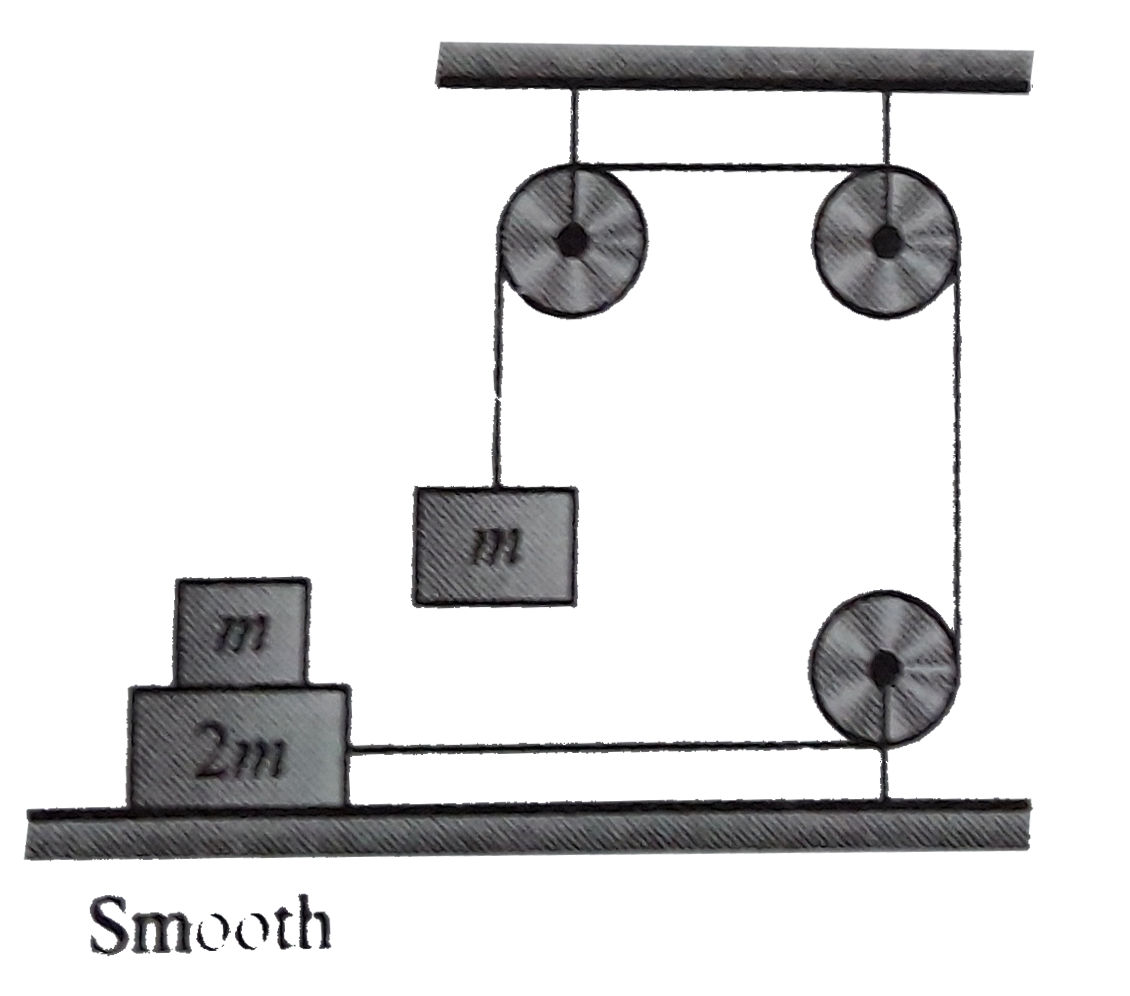 A12B1√2C14D13
A12B1√2C14D13
In the figure shown a ring of mass M and a block of mass m are in equilibrium. The string is light and pulley P does not offer any friction and coefficient of friction between pole and M is μ. The frictional force offered by the pole to M is

View SolutionIn the arrangement shown in Fig there is no friction between of mass 2m and ground but there is friction between the block of masses m is stationary with respect to block of mass 2m The value of friction between m and 2mis

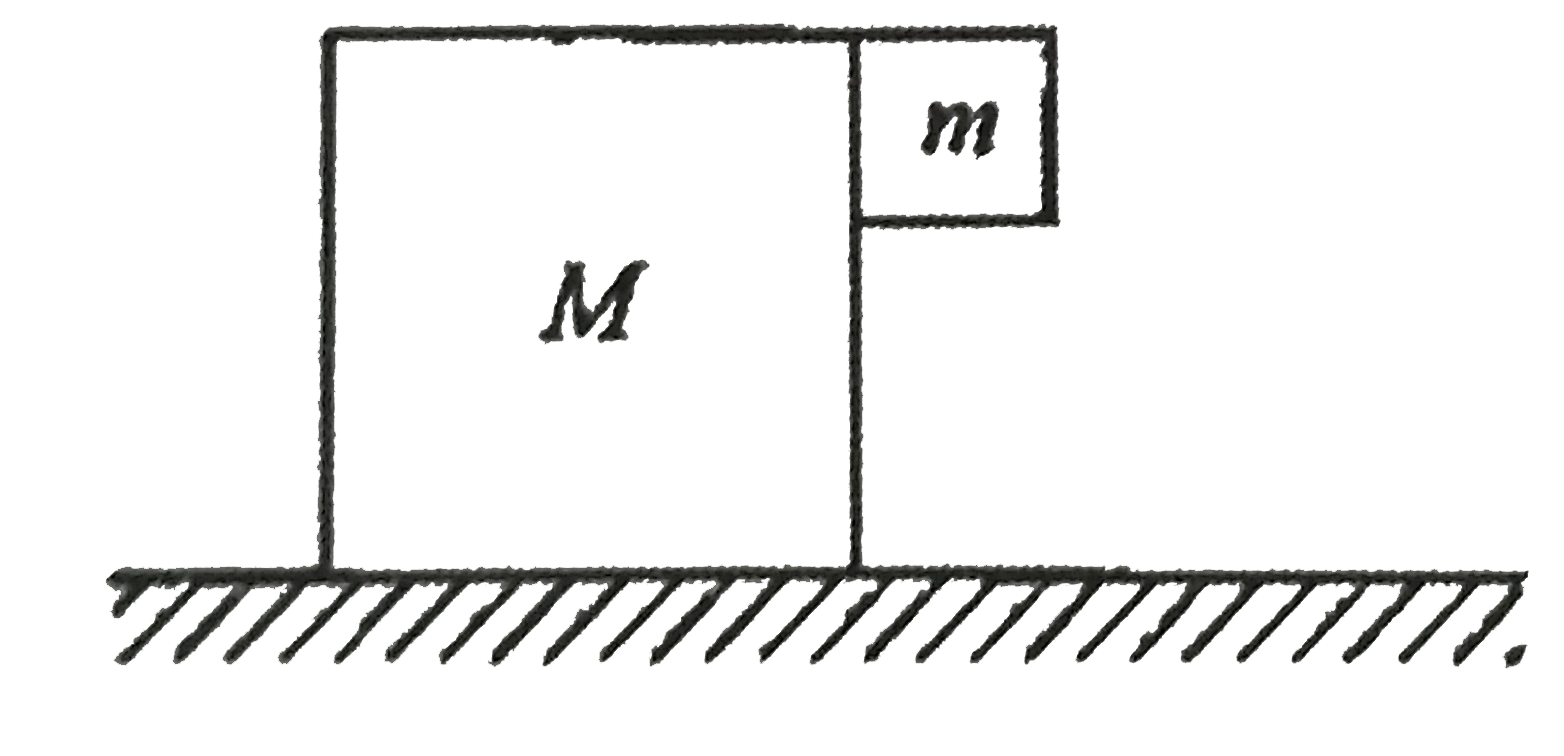
View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m
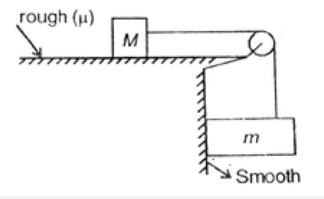
The minimum value of coefficient of friction μ such that system remains at rest , is
View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m

The minimum value of coefficient of friction μ such that system remains at rest , is
View SolutionFigure-2.84 shows a man ofmass M standing on a board of mass m.What minimum force is required to exert on string to slide the board. The friction coefficient between board and floor is μ and there is sufficient friction between man and board so that man does not slip.
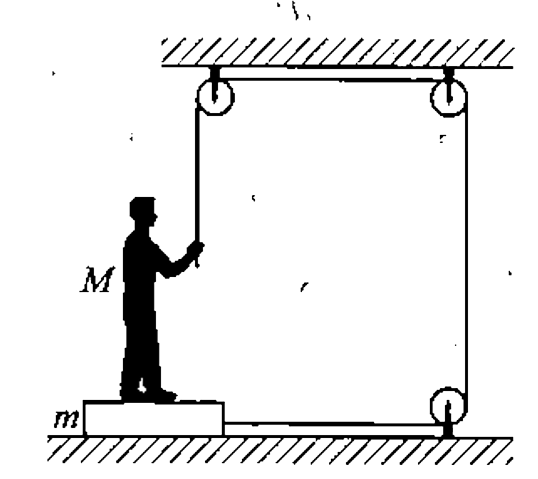
[μ(M+m)g1+μ]
View Solution
