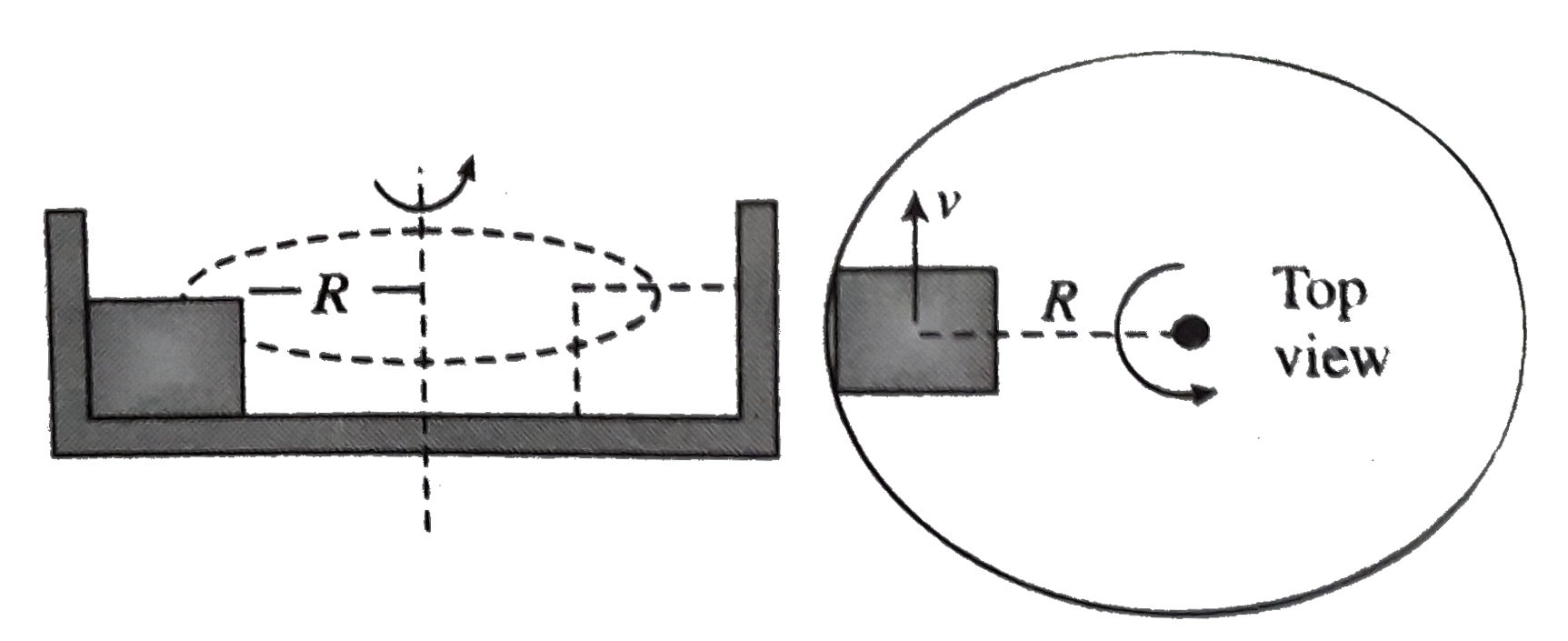
A block of mass m is revolving in a smooth horizontal plane with a constant speed v.If the radius of the circle path is R find the total contact force received by the block
mv2R
mg
m√v4R2+4g2
m√v4R2+g2
The correct Answer is:D
FBD Let N1N2↑ be the normal reaction offered by the vetrical and horizontal surface respectively N1 pushes the block toward the center of circle and N2 equilibrium the block in vertical by millifying the weight mg−2) force equation
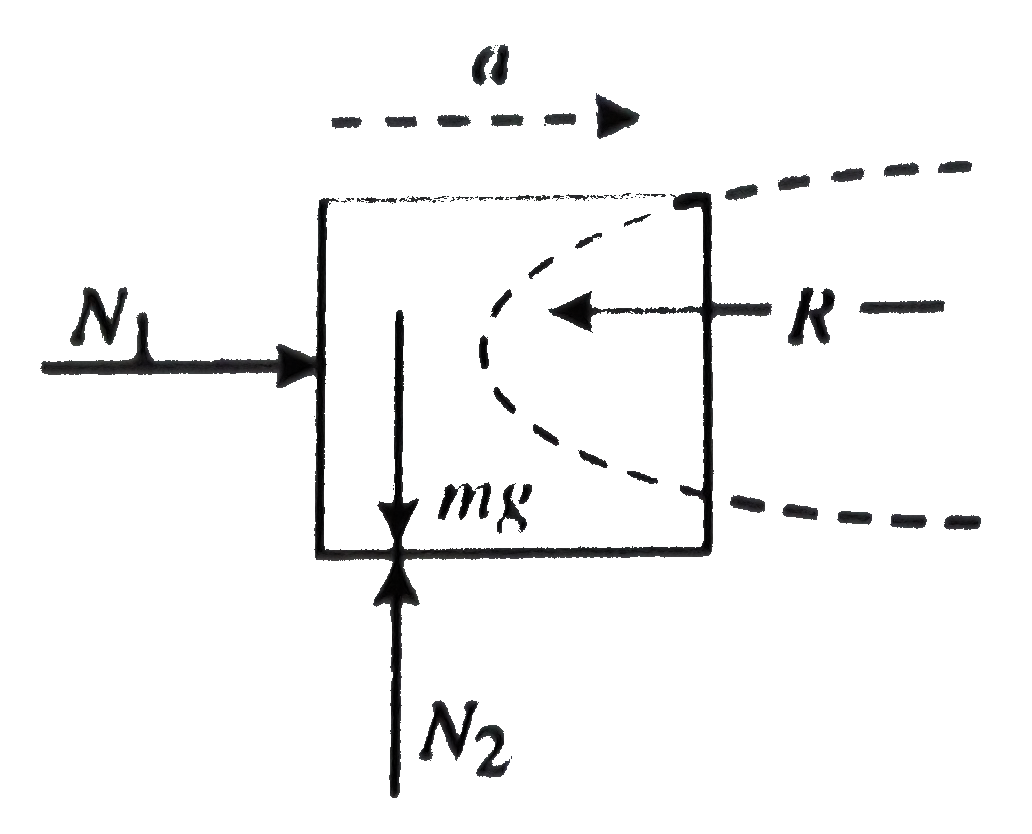
N1=ma1=mv2R...(i)
N2=mg ...(ii)
Hence the net reaction (contact) force is →N=→N1+→N2
∣∣→N∣∣=∣∣→N2∣∣=√N22+N21
Substinuting N1andN2 we have
N=m√v4R2+g2
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Multiple Correct
Explore 2 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Linked Comprehension
Explore 52 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Subjective
Explore 21 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Integer
Explore 5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
A bullted of mass m embeds itself in a block of mass M resting on a smooth horizontal surface, attached to a spring of force constant k. If the initial sped of the bullet is v0 along horizontal, find (a) the maximum compression of the spring and (b) the time forthe bullet - block system to come to rest.
View SolutionFigure shows a smooth track, a part of which is a circle of radius r. A block of mass m is pushed against a spring of spring constant k fixed at the left end and is then released. Find the initial compression of the spring so that the block presses the track with a force mg when it reaches the point P, where the radius of the track is horizontal.
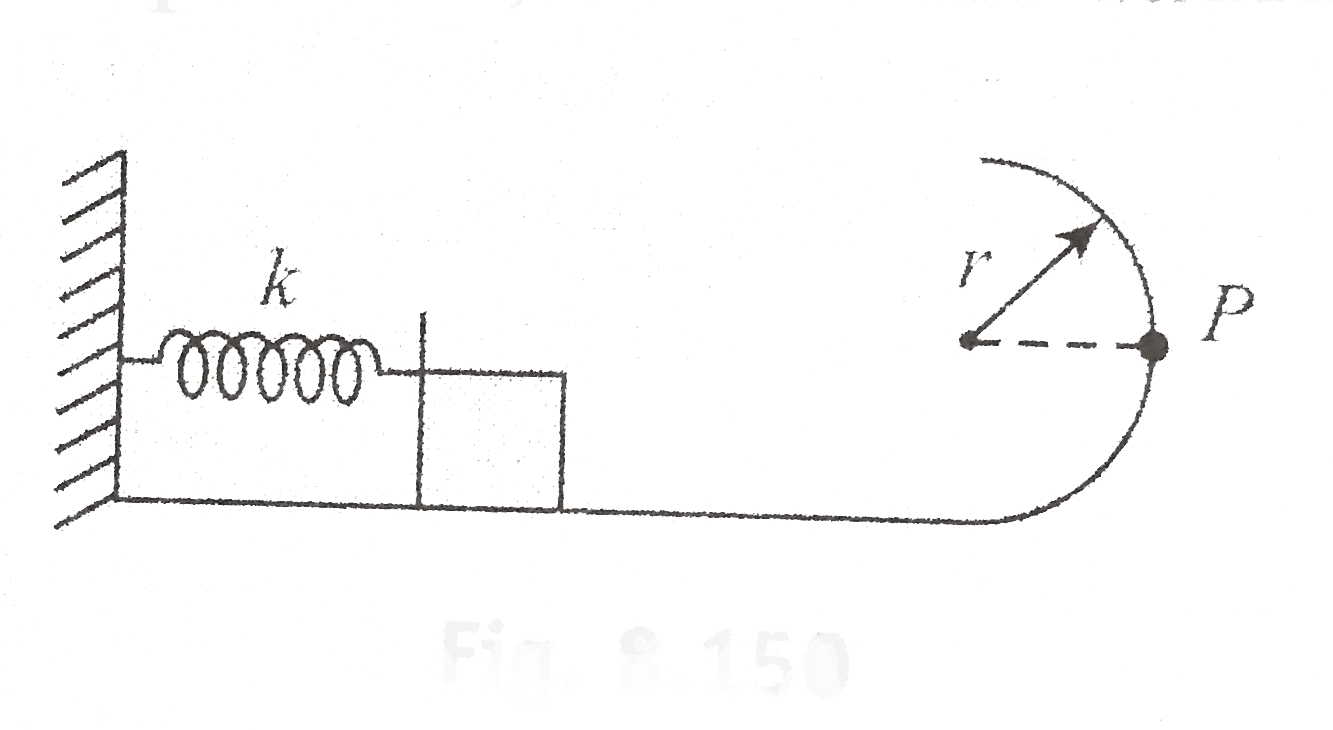
View Solution
Knowledge Check
A loop of mass M and radius R is rolling on a smooth horizontal surface with speed 'v'. It's total kinetic energy is
A1/2Mv2B3/2Mv2CMv2D1/2MR2ω2A block of mass M is resting on a smooth horizontal plane. One end of a uniform rope of mass M4 is fixed to the block , which pulled it in the horizontal direction by applying a force F at the other ends . The tension in the middle of the rope is
AF2BF5C910FDFA triangular block ABC of mass m and side 2a lies on a smooth horizontal plane is shown. There point masses of the m each strikes the block at A,B and C with speed as shown. After the collision the particle come to rest. Then
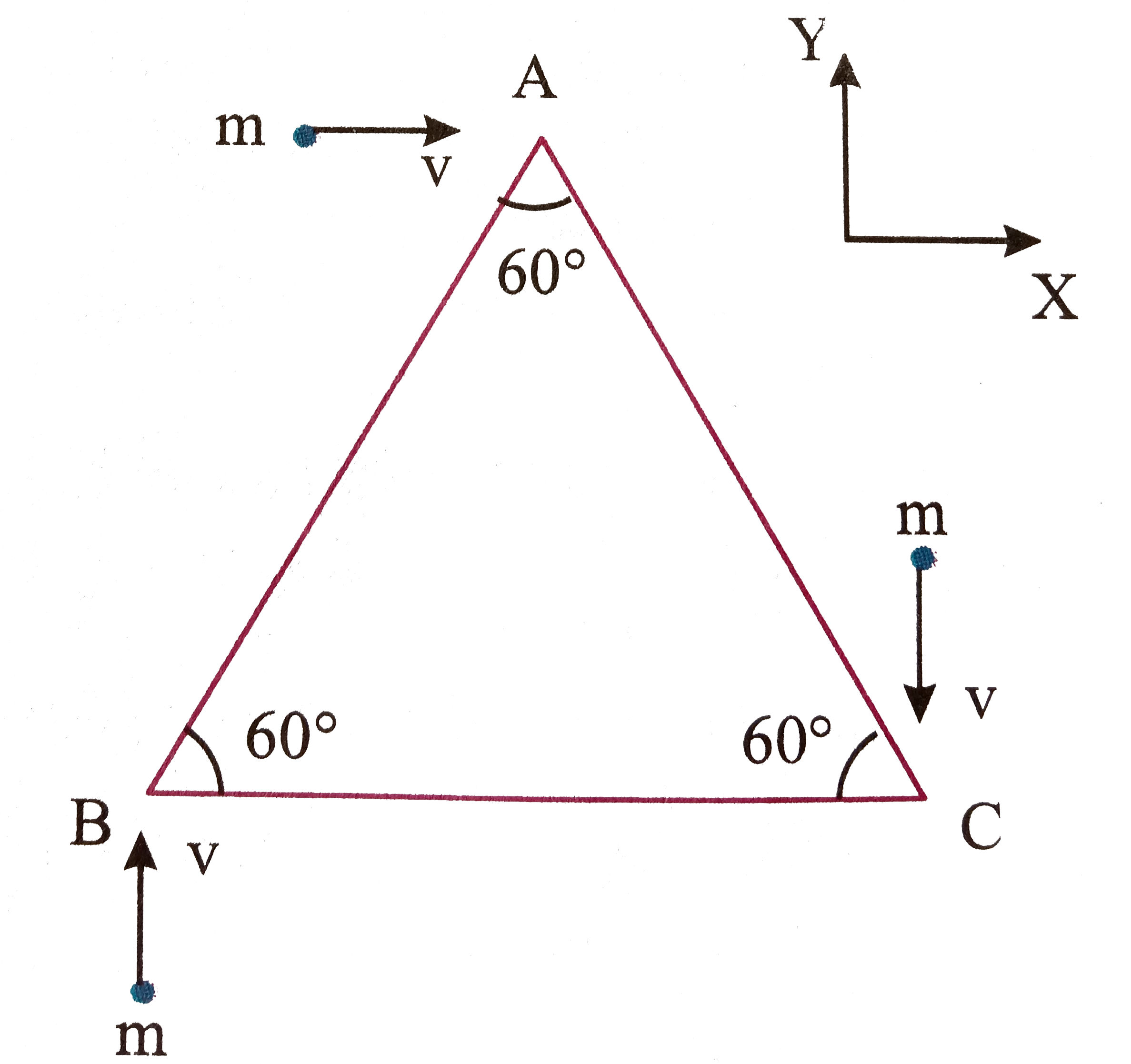 Athe centre of mass of ΔABC remains stationary after collisionBthe centre of mass of ΔABC moves with a velocityv along x-axis after collisionCthe triangular block rotates with an angular velocity ω=2√3mvaI about its centroid axis perpendicular to its planeDa point lying at a distance of (12√3ma) from centroid G on perpendicular bisector of BC is at rest just after collision
Athe centre of mass of ΔABC remains stationary after collisionBthe centre of mass of ΔABC moves with a velocityv along x-axis after collisionCthe triangular block rotates with an angular velocity ω=2√3mvaI about its centroid axis perpendicular to its planeDa point lying at a distance of (12√3ma) from centroid G on perpendicular bisector of BC is at rest just after collision
If A block is dragged on a smooth horizontal plane with the help of a light rope which moves with a velocity v as given in the figure .Then find the horizontal velocity of the block .
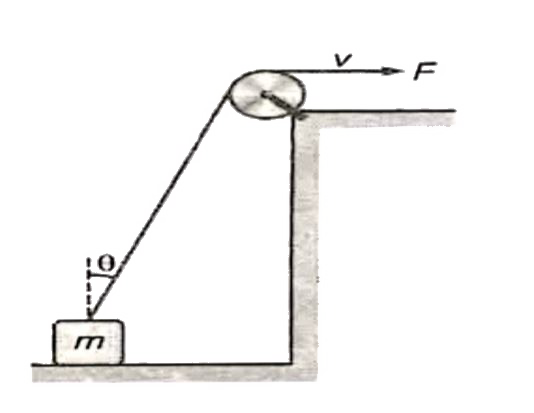
View SolutionFigure shows a smooth track, a part of which is a circle of radus R. As block of mass m is pushed against a sprng of spring constant k fixed at the left end and is then released. Find the initial compression of the spring so that the block presses the track with a force mg when it reaches the point P, where the radus of the track is horizontal.
View SolutionA block of mass m is revolving in a circle on a smooth table. The speed of the block is continuously reducing. The power delivered to the block :
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal.If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA block of mass M is pulled on a smooth horizontal table by a string making an angle θ with the horizontal as shown in figure. If the acceleration of the block is a find the force applied by the string and by the table N on the block.

View Solution