A block of mass 10kg is kept on a rought floor .The coefficient of friction between floor and block are μs=0.4 and μk=0.3 forcesF1=5N and F2=aN are applied on the block as shown in figure
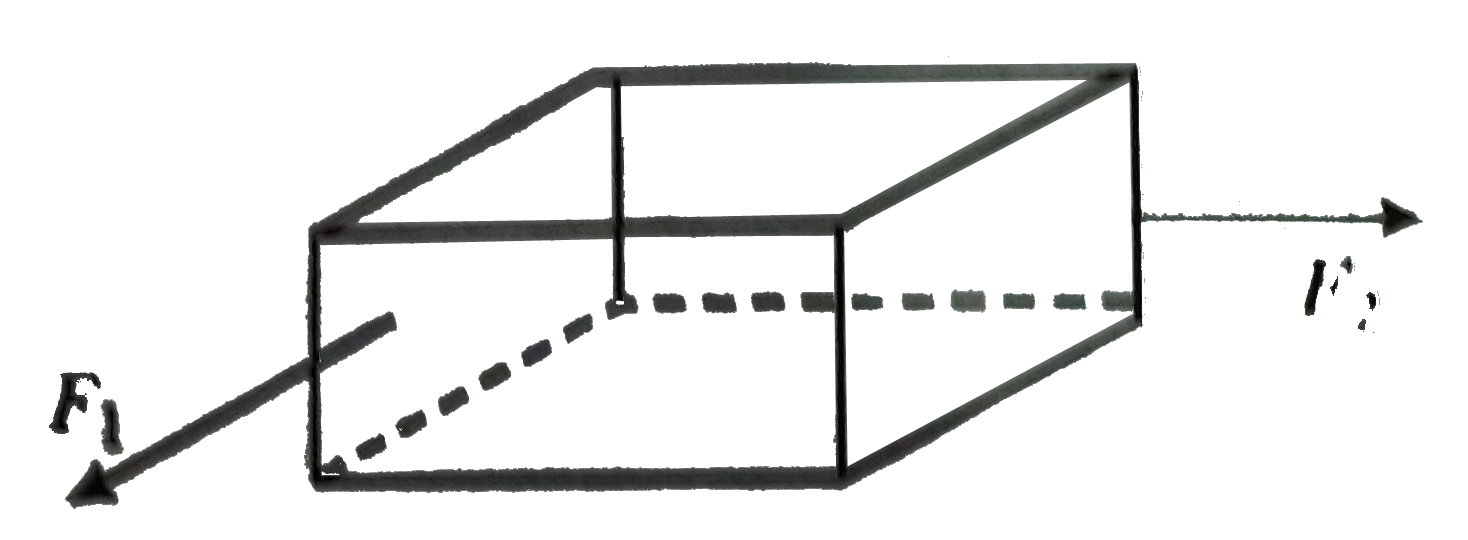
If F1=5N and F2=aN for what maximum value of a the motion of block impenride?
√31N
√26N
√41N
√36N
The correct Answer is:c
Net force F=√F21+F22=√41N
f1=0.4×10g=40Nfk=0.3×10g=30N
net force is less than f0 hence
Required friction force = applined force=√41N
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer6videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - True And False4videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct2videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
Similar Questions
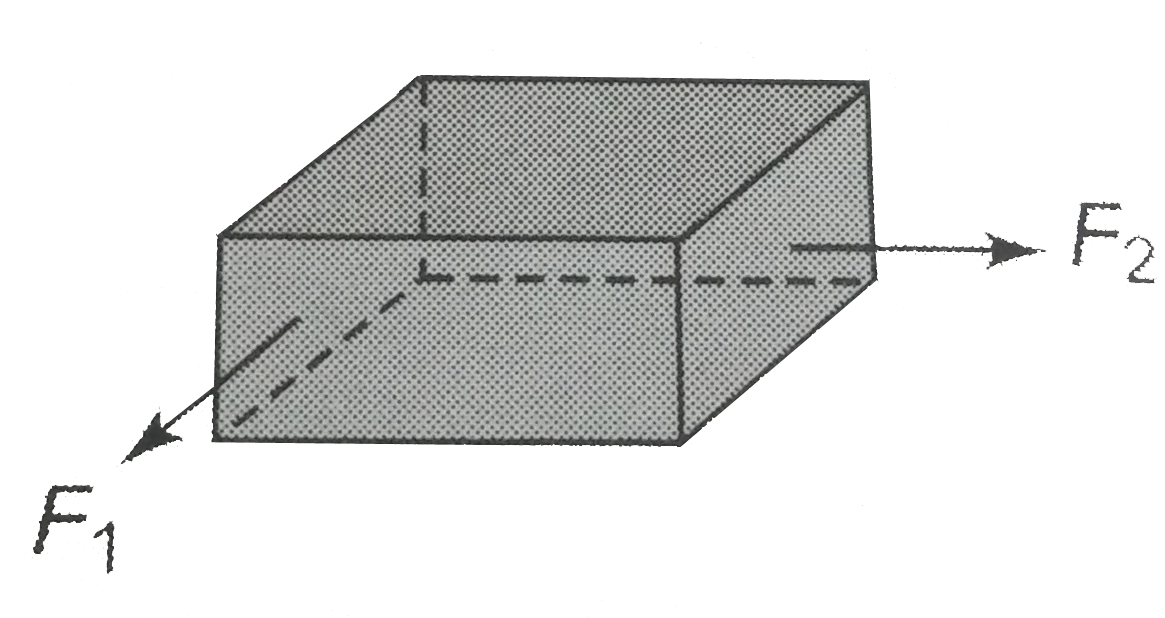
A block of mass 8kg is kept on a rough floor. The coefficients of friction are μs=0.5 and μk=0.4. Force F1=15N and F2=20N are applied on the block as shown.
(a) Find the magnitude and the direction of friction force .
(b) If F1=30N,F2=40N, find the acceleration of the block.
 View Solution
View SolutionA block of mass m=4kg is placed over a rough inclined plane as shown in fig . The coefficient of friction between the block and the plane μ=0.5 A force F=10N is applied on the block at an angle of 30∘. Find the contact force between the block and the plane.
k
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m=4kg is placed oner a rough inclined plane as shown in figure. The coefficient of friction between the block and the plane is μ=0.5 . A force F=10N is applied on the block at an angle of 30∘ .
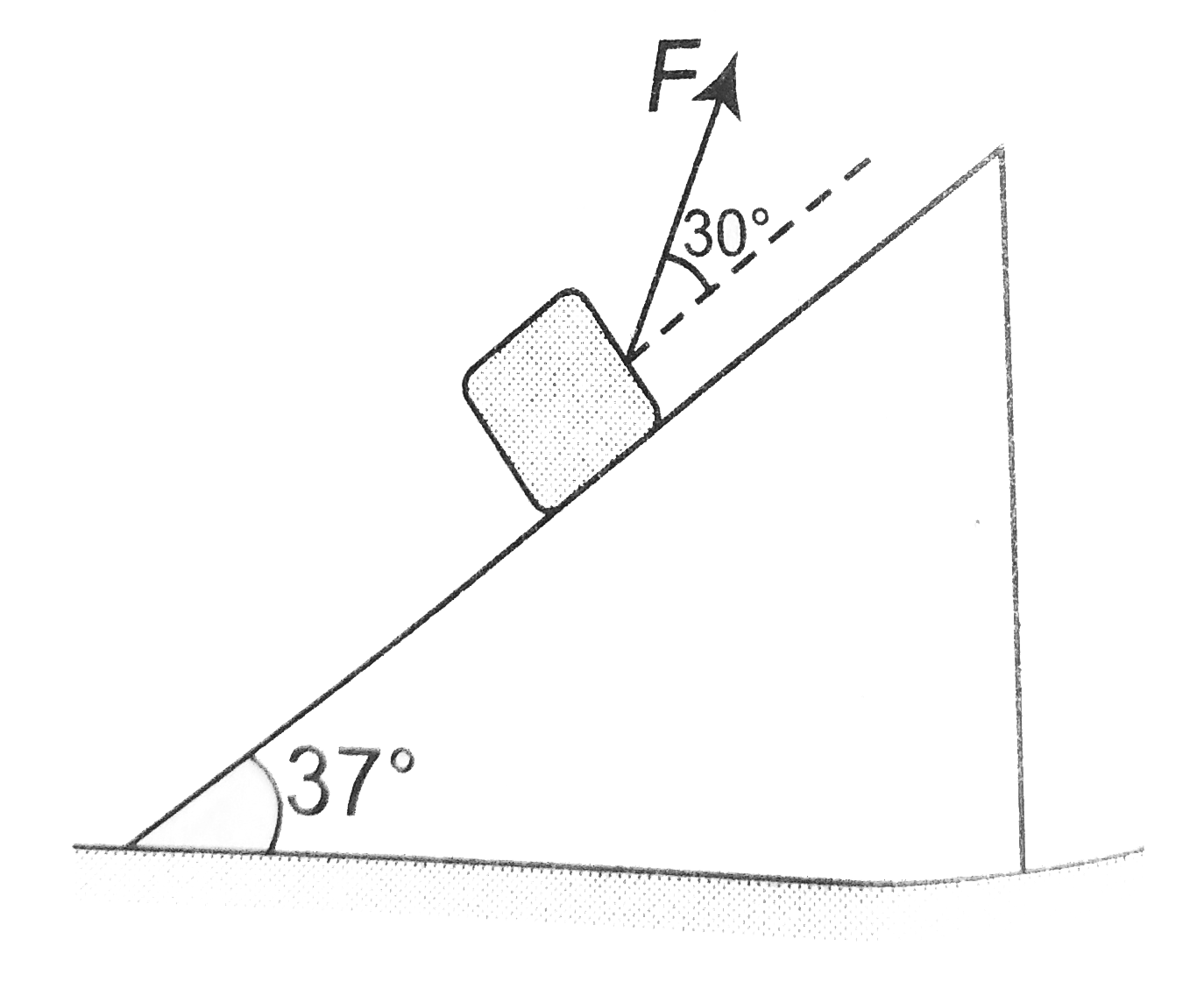 Astatic in nature in the direction up the plane and have the value 30.2NBstatic in nature in the direction down the plane and have the value 30.2NCkinetic in nature in the direction up the plane and have the value 30.2NDNone of these
Astatic in nature in the direction up the plane and have the value 30.2NBstatic in nature in the direction down the plane and have the value 30.2NCkinetic in nature in the direction up the plane and have the value 30.2NDNone of these - Question 2 - Select One
A block of mass 2 kg is at rest on a floor . The coefficient of static friction between block and the floor is 0.54. A horizonatl force of 2.8 N is applied to the block . What should be the frictional force between the block and the floor ? ( take , g=10m/s2)
A8.8NB5.8NC2.8ND10.8N - Question 3 - Select One
A block of mass 5kg is lying on a rough horizontal surface. The coefficient of static and kinetic friction are 0.3 and 0.1 and 10m/s−2. If a horizontal force of 50N is applied on the block, the frictional force is
A25NB5NC10NDZero
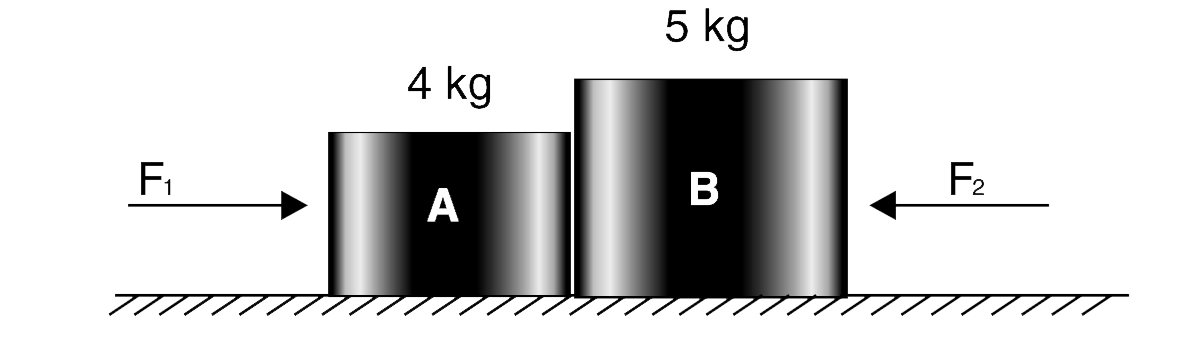
Two rectangular blocks A and B are placed on a horizontal surface at a very small separation. The masses of the blocks are mA=4 kg and mB=5 kg. Coefficient of friction between the horizontal surface and both the blocks is μ=0.4. Horizontal forces F1 and F2 are applied on the blocks as shown. Both the forces vary with time as F1=15+0.5t
F2=2t
Where ‘t’ is time in second.
Plot the variation of friction force acting on the two blocks (fAandfB) vs time till the motion starts. Take rightward direction to be positive for B and leftward direction to be positive forfA.
 View Solution
View SolutionThe coefficient of friction between the blocks are μs=0.3 and μk=0.2. (a) Find the maximum value of F so that the blocks move together. (b) If force F is twice the value found in (a), find the acceleration of each block.
 View Solution
View SolutionThe coefficient of friction between the blocks is 0.5. Find the acceleration of each block if Fis(a)21N,(b)35 Nand(c)40 N.
 View Solution
View SolutionA block of mass 2 kg is at rest on a floor . The coefficient of static friction between block and the floor is 0.54. A horizonatl force of 2.8 N is applied to the block . What should be the frictional force between the block and the floor ? ( take , g=10m/s2)
View SolutionA block of mass 2kg is kept on the floor. The coefficient of static friction is 0.4 . If a force F of 2.5N is applied on the block as shown in the figure, the frictional force between the block and the floor will be.
 View Solution
View Solution

