Two blocks of masses m and M connected by a light spring of stiffness k, are kept on a smooth horizontal surface as shown in figure. What should be the initial compression of the spring so that the system will be about to break off the surface, after releasing the block m1?
To solve the problem, we need to determine the initial compression of the spring required for the system to just break off the surface after releasing the block of mass M.
1. Understand the Forces Involved:
When the spring is compressed, it stores potential energy. Upon releasing the block M, the spring will exert a force on both blocks m and M. The system will break off the surface when the force exerted by the spring equals the weight of the block M.
2. Calculate the Potential Energy in the Spring:
The potential energy U stored in a compressed spring is given by the formula:
U=12kx2
where k is the spring constant and x is the compression of the spring.
3. Determine the Condition for Breaking Off:
The system will break off the surface when the upward force from the spring equals the weight of the block M:
Fspring=Mg
where g is the acceleration due to gravity.
4. Relate the Spring Force to Compression:
The force exerted by the spring when compressed by x is given by Hooke's Law:
Fspring=kx
Setting this equal to the weight of block M:
kx=Mg
5. Solve for the Compression x:
Rearranging the equation gives:
x=Mgk
This equation tells us the initial compression x needed in the spring for the system to break off the surface after releasing block M.
Final Answer:
The initial compression of the spring required for the system to break off the surface after releasing block M is:
x=Mgk
When the spring is compressed, it stores potential energy. Upon releasing the block M, the spring will exert a force on both blocks m and M. The system will break off the surface when the force exerted by the spring equals the weight of the block M.
The potential energy U stored in a compressed spring is given by the formula:
U=12kx2
where k is the spring constant and x is the compression of the spring.
The system will break off the surface when the upward force from the spring equals the weight of the block M:
Fspring=Mg
where g is the acceleration due to gravity.
The force exerted by the spring when compressed by x is given by Hooke's Law:
Fspring=kx
Setting this equal to the weight of block M:
kx=Mg
Rearranging the equation gives:
x=Mgk
This equation tells us the initial compression x needed in the spring for the system to break off the surface after releasing block M.
The initial compression of the spring required for the system to break off the surface after releasing block M is:
x=Mgk
Topper's Solved these Questions
Similar Questions
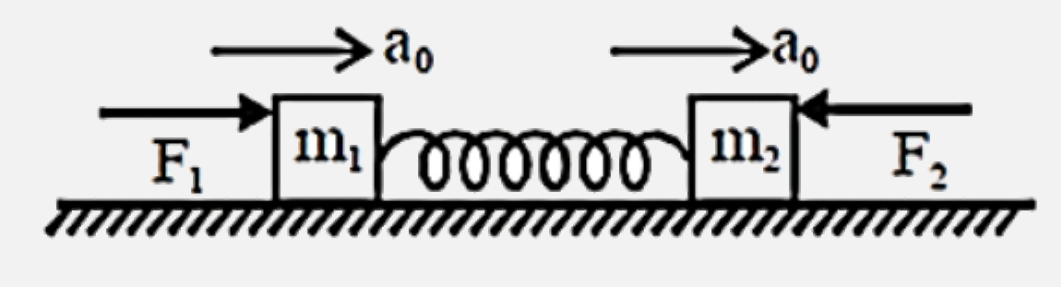
Two blocks of masses m1andm2 being connected with a light spring of stiffness k are driven with forces F1andF2 on a smooth horizontal plane.
 View Solution
View SolutionTwo blocks of masses m1 and m2, connected by a weightless spring of stiffness k rest on a smooth horizontal plane as shown in Fig. Block 2 is shifted a small distance x to the left and then released. Find the velocity of centre of mass of the system after block 1 breaks off the wall.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
Athe momentum of each particle remains constant separatelyBthe magnitude of momentums of each body are equal to each otherCthe mechanical energy of system remains constantDboth (C) and (B) are correct - Question 2 - Select One
A block of mass m compresses a spring iof stifffness k through a distacne l/2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is
 A2π√mkB(π+4)√mkC(1+π)√mkDNone of these
A2π√mkB(π+4)√mkC(1+π)√mkDNone of these
A block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released
 View Solution
View SolutionTwo bars of masses m1 and m2 connected by a weightless spring of stiffness ϰ (figure) rest on a smooth horizontal plane.

Bar 2 is shifted a small distance x to the left and then released. Find the velocity of the centre of inertia of the system after bar 1 breaks off the wall.View SolutionTwo blocks of masses m and m' are connected by a light spring on a horizontal frictionless table . The spring is compressed and then released . Find the ratio of acceleration of masses .
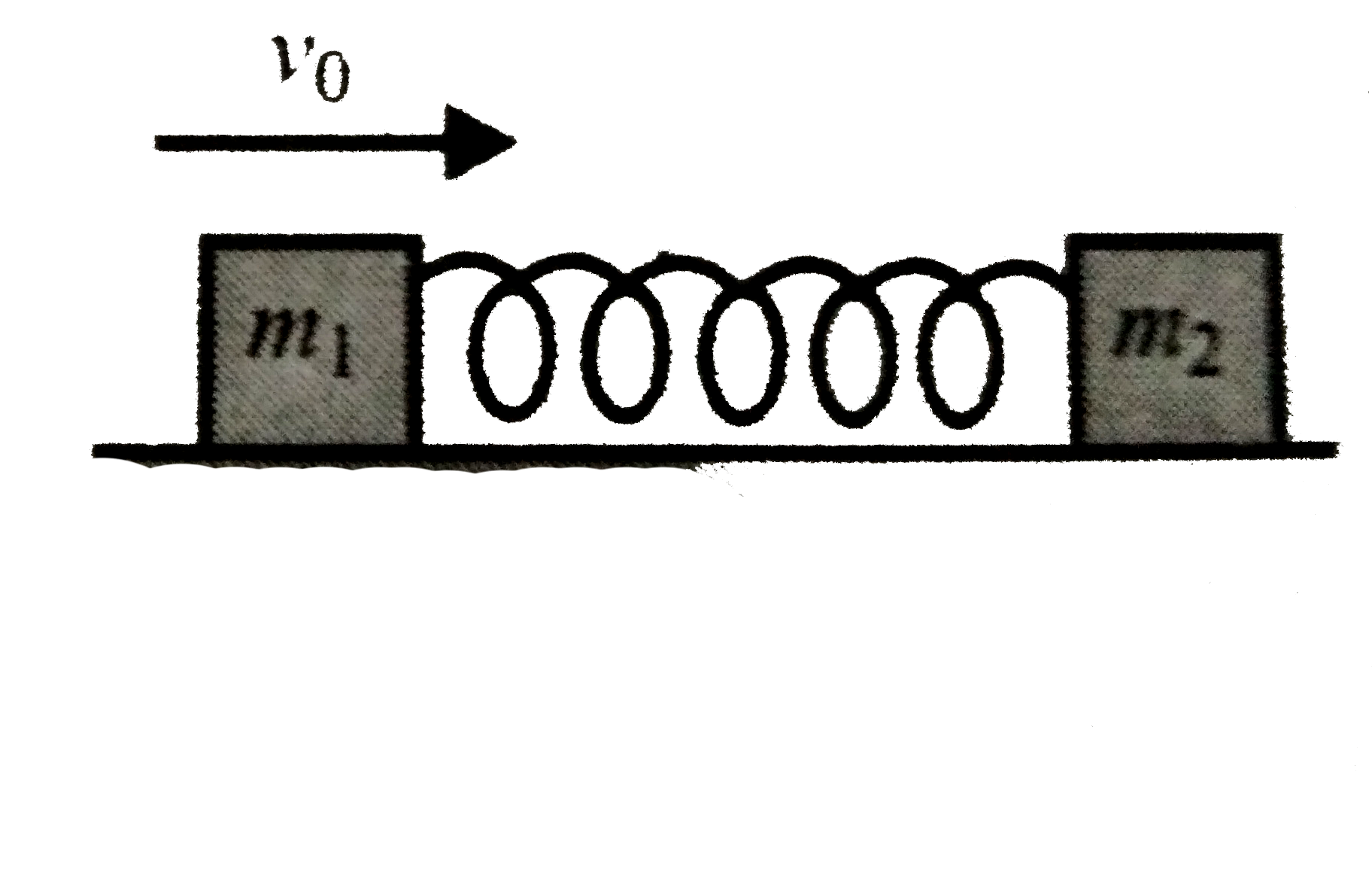
View SolutionTwo smooth blocks of mases m1andm2 attached with an ideal spring of stiffness k and kept on hrozontal surface. If m1 is projected with a horizontal velocity v0. Find the maximum compression of the spring.
 View Solution
View SolutionTwo blocks of masses m1 and m2 interconnect with a spring of stiffness K, are kept on as smooth horizontal surface. Find out the ratio of velocity, displacement, kinetic energy and acceleration block with mass m1 of block with mass m2.
View SolutionTwo blocks A and B of masses m and 2m respectively are connected together by a light spring of stiffness k and then placed on a smooth horizontal surface. The blocks are pushed towards each other such that spring gets compressed by a length x0 and then released from rest. Find the work done on the block A by the spring, by the time the spring acquires its natural length.
View Solution

