Two blocks A and B of masses m and 2m respectively are connected together by a light spring of stiffness k and then placed on a smooth horizontal surface. The blocks are pushed towards each other such that spring gets compressed by a length x0 and then released from rest. Find the work done on the block A by the spring, by the time the spring acquires its natural length.
from COM
mvA=2mvB
⇒vB=vA2
from COE
12kx20=12mv2A+12×2mv2A4=12mv2A(1+12)
⇒12kx20=12mv2A×32⇒12mv2A=kx203
Topper's Solved these Questions
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Objective problems
215 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Assertion & Reason
15 Videos
- GENERAL PHYSICSBOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE
3 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question
2 Videos
Similar Questions
Two blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View SolutionTwo blocks A and B of masses m and 2m, respectively , are connected by a massless spring of force constant k and are placed on a smooth horizontal plane. The spring is stretched by an amount x and then released . The relative velocity of the blocks when the spring comes to its natural length is

View Solution
Knowledge Check
Two blocks A and B of mass m and 2m are connected together by a light spring of stiffness k. The system is lying on a smooth horizontal surface with block A in contact with a fixed vertical wall as shown in the figure. The block B is pressed towards the wall by a distance x0 and then released. There is not friction anywhere. If spring takes time Δt to aquire its natural length then average force on the block A by the wall is
 A(a) zeroB(b) √2mkΔtx0C(c) √mkΔtx0D(d) √3mkΔtx0
A(a) zeroB(b) √2mkΔtx0C(c) √mkΔtx0D(d) √3mkΔtx0Two blocks A and B of the same mass are connected to a light spring and placed on a smooth horizontal surface B is given velocity v0 (as shown in the figure) when the spring is in natural length. In the subsequent motion.
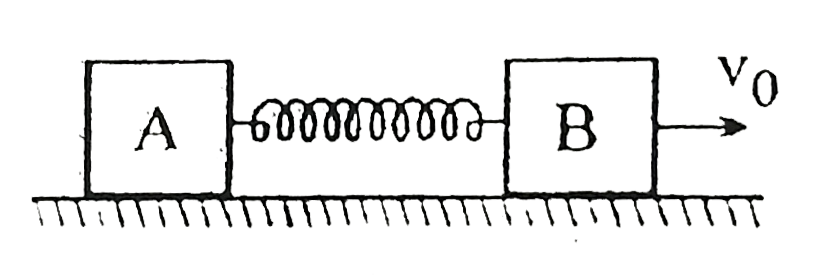 Athe maximum velocity of B will be v0Bas seen from ground, A can move towards right onlyCthe spring will have maximum extension when A and B both stopDthe spring will be at natural length again when B is at rest
Athe maximum velocity of B will be v0Bas seen from ground, A can move towards right onlyCthe spring will have maximum extension when A and B both stopDthe spring will be at natural length again when B is at restA light spring of force constant 'K' is held between two blocks of masses 'm' and '2m'. The two blocks and the spring system rests on a smooth horizontal floor. Now th blocks are moved towards each other compressing the springs by 'x' and suddenly released. The relative velocity between the blocks when the spring attains its natural length will be
A(√3K2m)xB(√2K3m)xC(√K3m)xD(√K2m)x
Two blocks of masses m and M connected by a light spring of stiffness k, are kept on a smooth horizontal surface as shown in figure. What should be the initial compression of the spring so that the system will be about to break off the surface, after releasing the block m1?
View SolutionTwo bolcks A & B are connected by a spring of stiffness 512N/m and placed on a smooth horizontal surface. Initially the spring has its equilibrium length. The indicated velocities are imparted to A & B. Find the maximum extension in the spring?
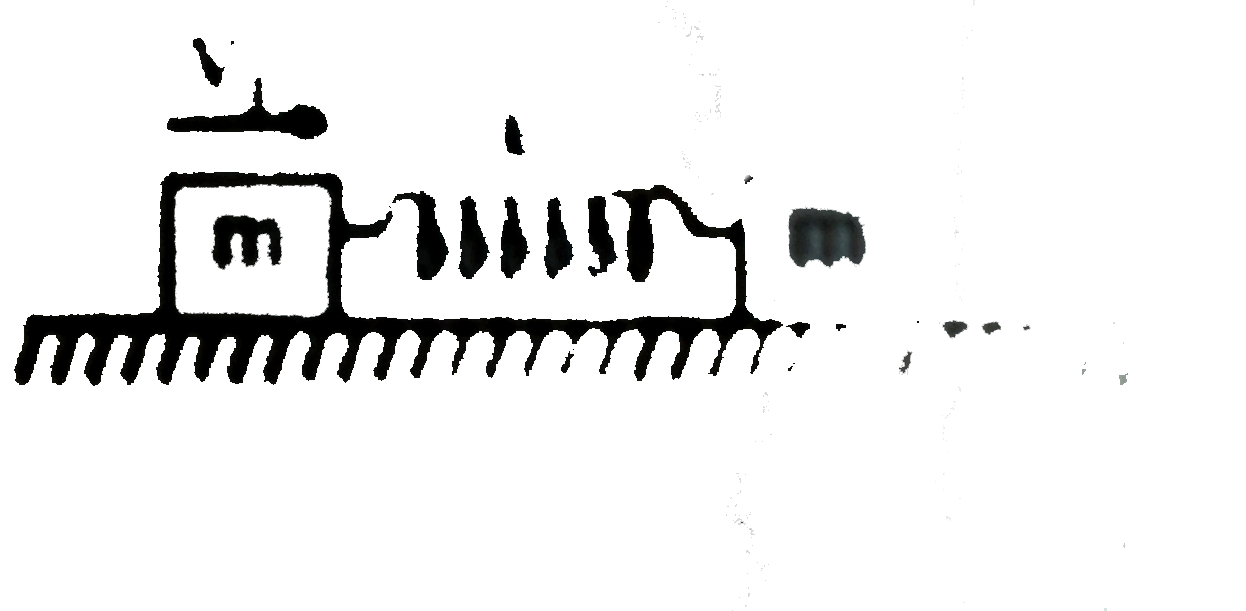
View SolutionTwo blocks of masses m and m' are connected by a light spring on a horizontal frictionless table . The spring is compressed and then released . Find the ratio of acceleration of masses .
View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a massless spring of spring constant K. This system lies over a smooth horizontal surface. At t=0 the bolck A has velocity u towards right as shown while the speed of block B is zero, and the length of spring is equal to its natural length at that at that instant.

Column IColumn II(A)The velocity of block A(P)can never be zero(B)The velocity of block B(Q)may be zero at certain instants of time(C)The kinetic energy of system of two block(R)is minimum at maximum compression of spring(D)The potential energy of spring(S)is maximum at maximum extension of spring
View Solution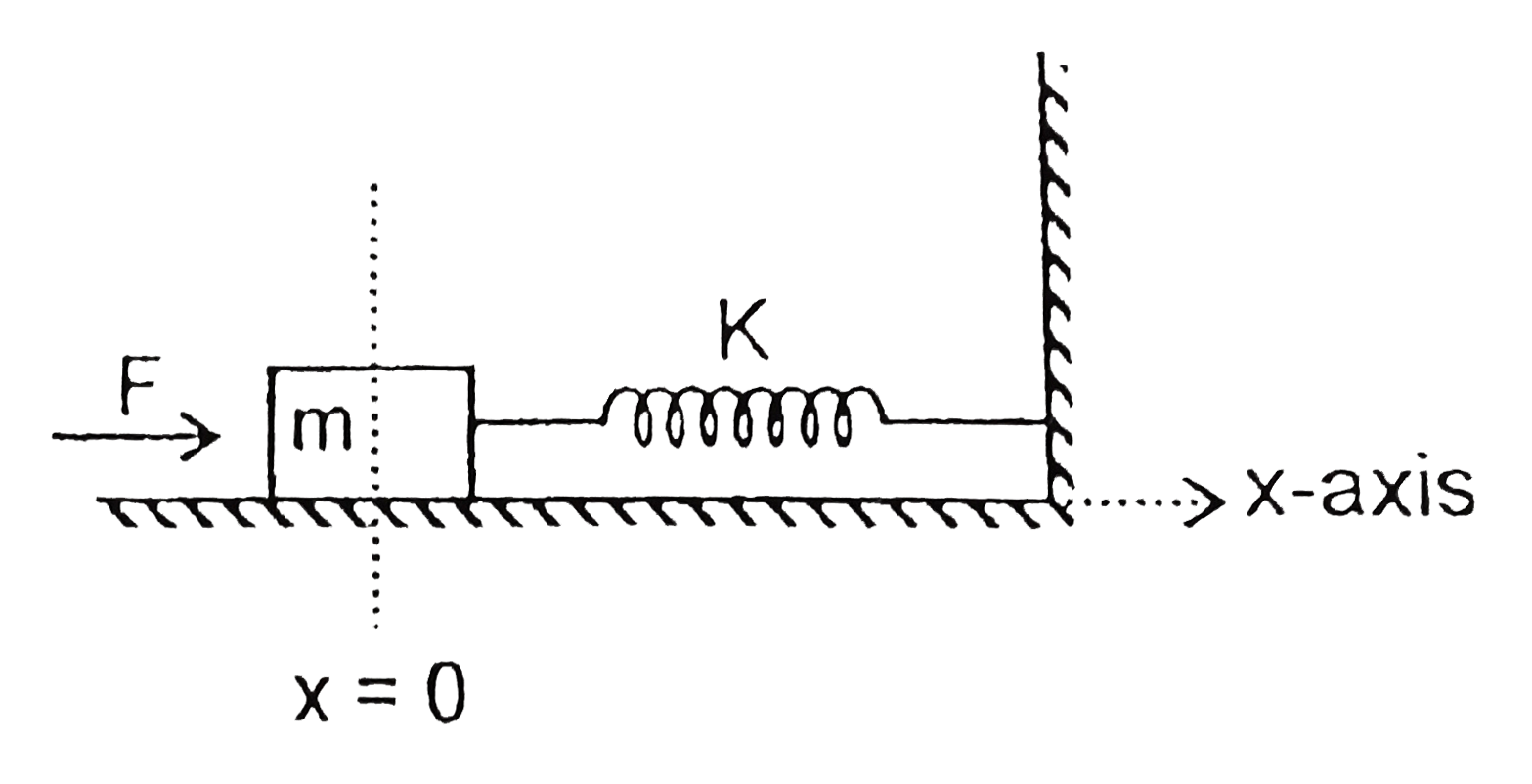
A block of mass m connected to a spring of stiffness k is placed on horizontal smooth surface. When block is at x=0, spring is in natural length. The block is also subjected to a force F=k|x|∘ then
View Solution
