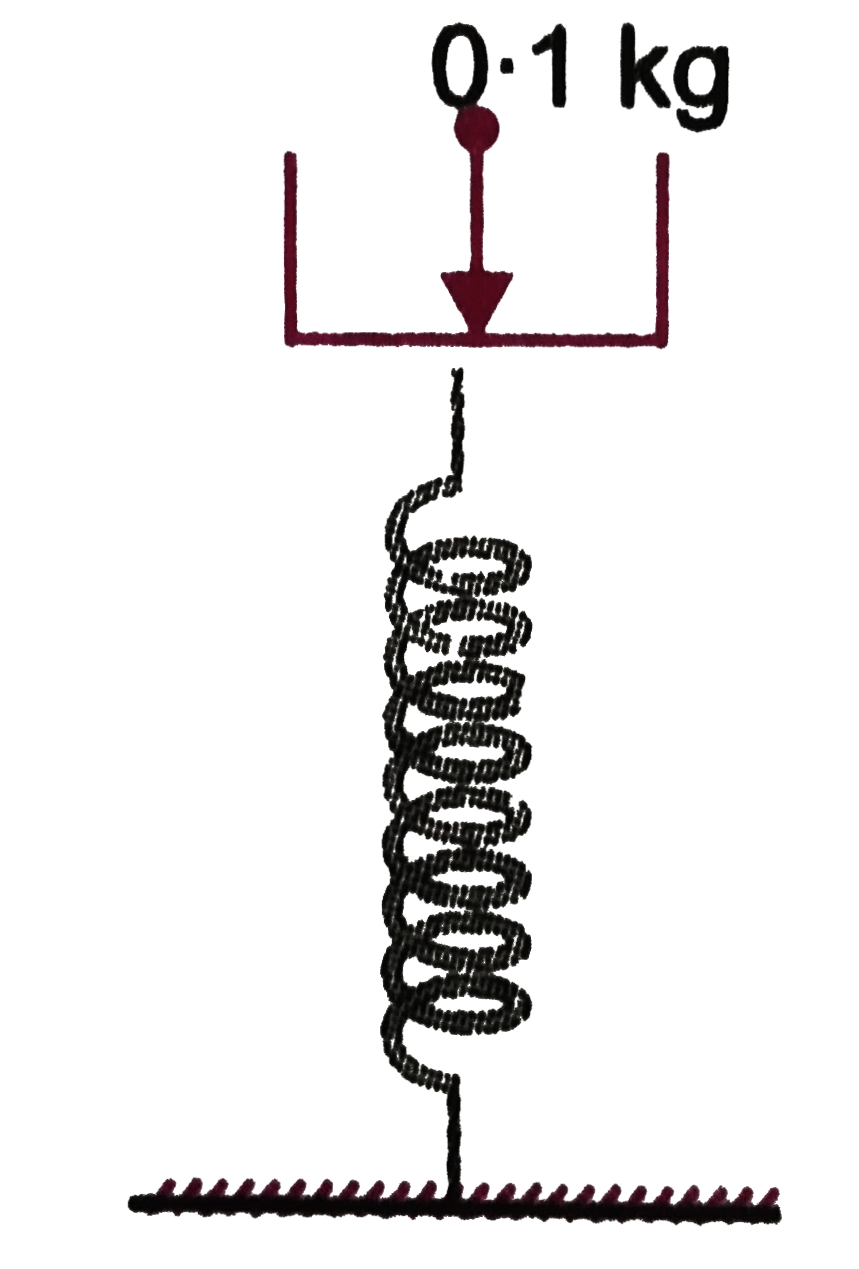
A massless platform is kept on a light elastic spring as shown in figure. When a small stone of mass 0.1 kg is dropped on the pan from a height of 0.24 m, the spring compresses by 0.01m. From what height should the stone be droppped to cause a compression of 0.04m in the spring ?

A

$0.96 m$

B

$2.96 m$

C

$3.96 m$

D

$0.48 m$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Let the particle be dropped from a height h and the spring be compressed by y. According to the conservation of mechanical energy, loss in PE of the particle=gain in elastic potential energy of the spring.
$m g (h + y) = \frac{1}{2} k y^{2}$
Now, as the particle and spring are same for second case,
$\frac{h_{1} + y_{1}}{h_{2} + y_{2}} = {(\frac{y_{1}}{y_{2}})}^{2}$ or $(\frac{0.24 + 0.01}{h_{2} + 0.04}) = {(\frac{0.01}{0.04})}^{2}$
Solving, we get $h_{2} = 3.96 m$

|

Updated on:21/07/2023

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A massless platform is kept on a light elastic spring, as shown in the figure. When particle of mass 0.1 kg is dropped on the pan from a height of 0.24 m, the particle strikes the pan, and the spring is compressed by 0.01 m. From what height should the particle be dropped to cause a compression of 0.04 m?

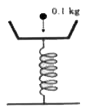A0.96 m
B2.96 m
C3.96 m
D0.48 m
Question 2 - Select One
The two masses $m_{1}$ and $m_{2}$ are joined by a spring as shown. The system is dropped to the ground from a height. The spring will be

AStreched when $m_{2} > m_{1}$
BCompressed when $m_{2} < m_{1}$
Cneither compressed not stretched only when $m_{1} = m_{2}$
Dneither compressed not stretched regardless of the values of $m_{1}$ and $m_{2}$ .
Question 3 - Select One
When a spring is compressed by 0.05 m a restoring force of 10 N is developed in it. Then the force constant of the spring is
A50 N/m
B100 N/m
C150 N/m
D200 N/m

CENGAGE PHYSICS-WORK, POWER & ENERGY-Single Correct

Home
Ask Doubt
Profile