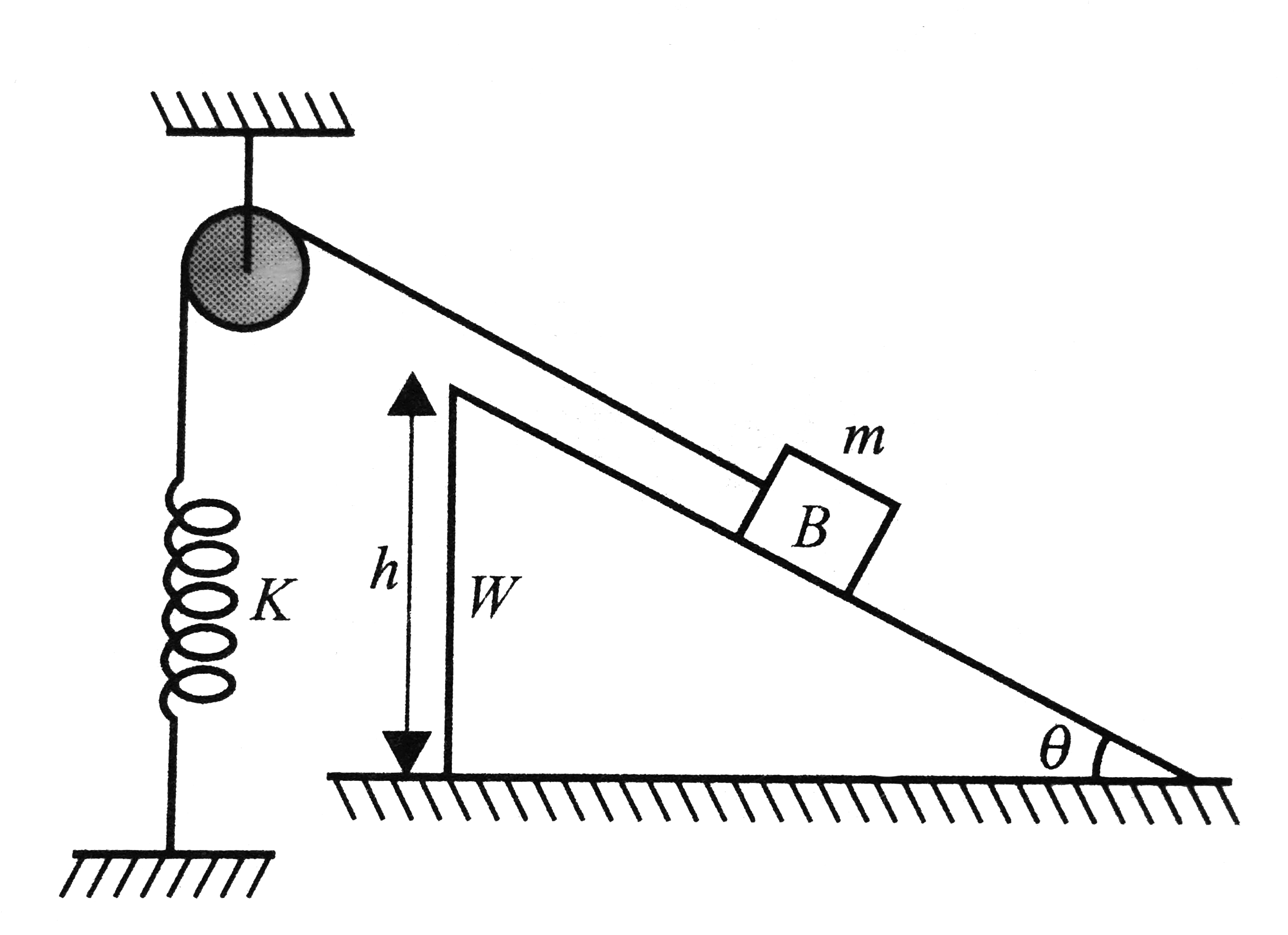
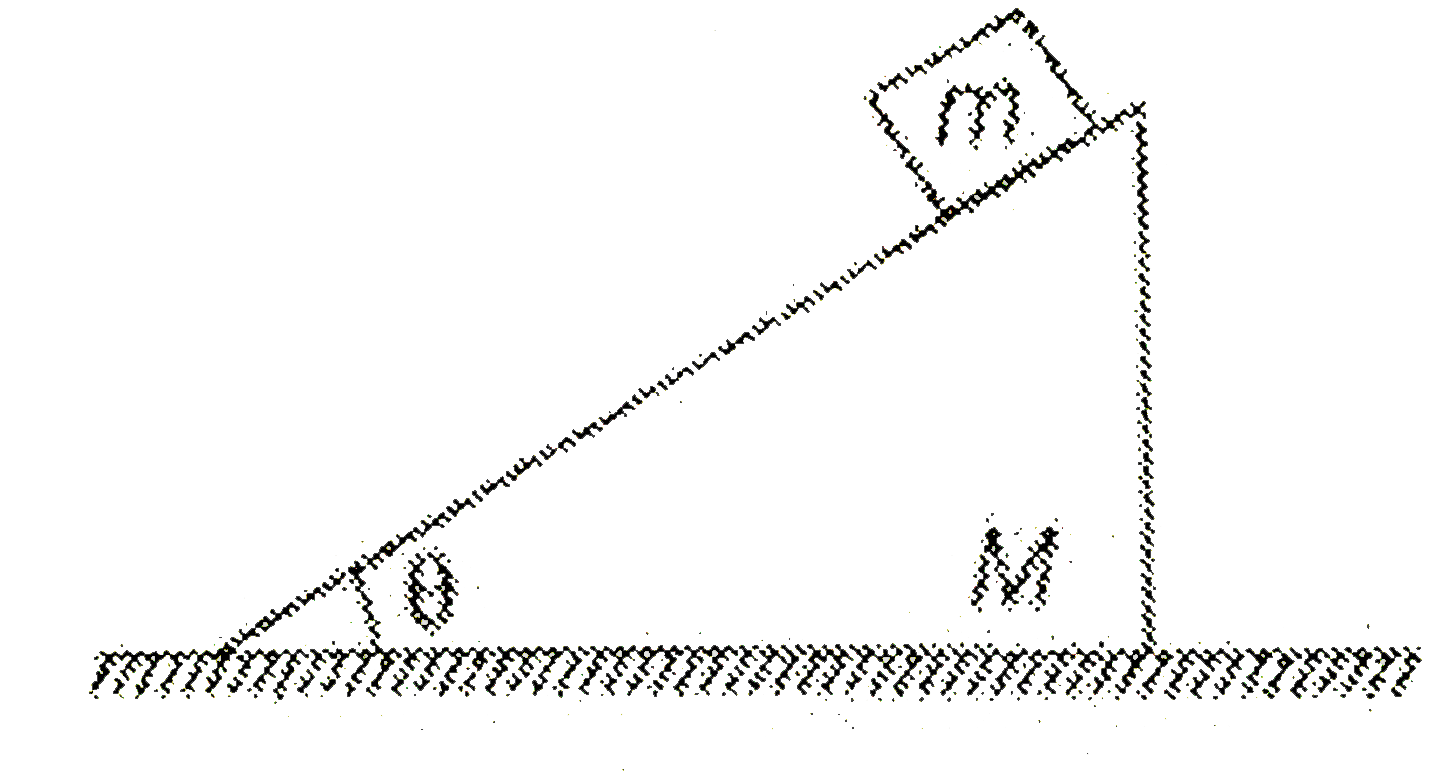
In figure, the pulley shown is smooth. The spring and the string are light. Block B slides down from the top along the fixed rough wedge of inclination θ. Assuming that the block reaches the end of the wedge, find the speed of the block at the end. Take the coefficient of friction between the block and the wedge to be μ and that the spring was relaxed when the block was released from the top of the wedge.
The correct Answer is: ⎷2m[mgh−12K(hsinθ)2−μmghcotθ]
Here block will loose the gravtitational potential energy. This energy will be divided in three ways.
a. Some part will be converted in the KE of block
b. Some part will go into spring
c. Remaining part will be used to do work against friction.
By energy conservation:
mgh=12mv2+12K(hsinθ)2+μmgcosθ(hsinθ)
⇒v=
⎷2m[mgh−12K(hsinθ)2−μmghcotθ]
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Single Correct
100 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.5
15 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
In the figure shown the pulley is smooth . The spring and the string are light. The block 'B' slides down from the top along the fixed rought wedge of inclination θ. Assuming that the block reaches the end of the wedge. Find the speed of the block at the end. Take the coefficient of friction between the block and the wedge to be μ and the spring was relaxed when the block was relased from the top of the wedge.
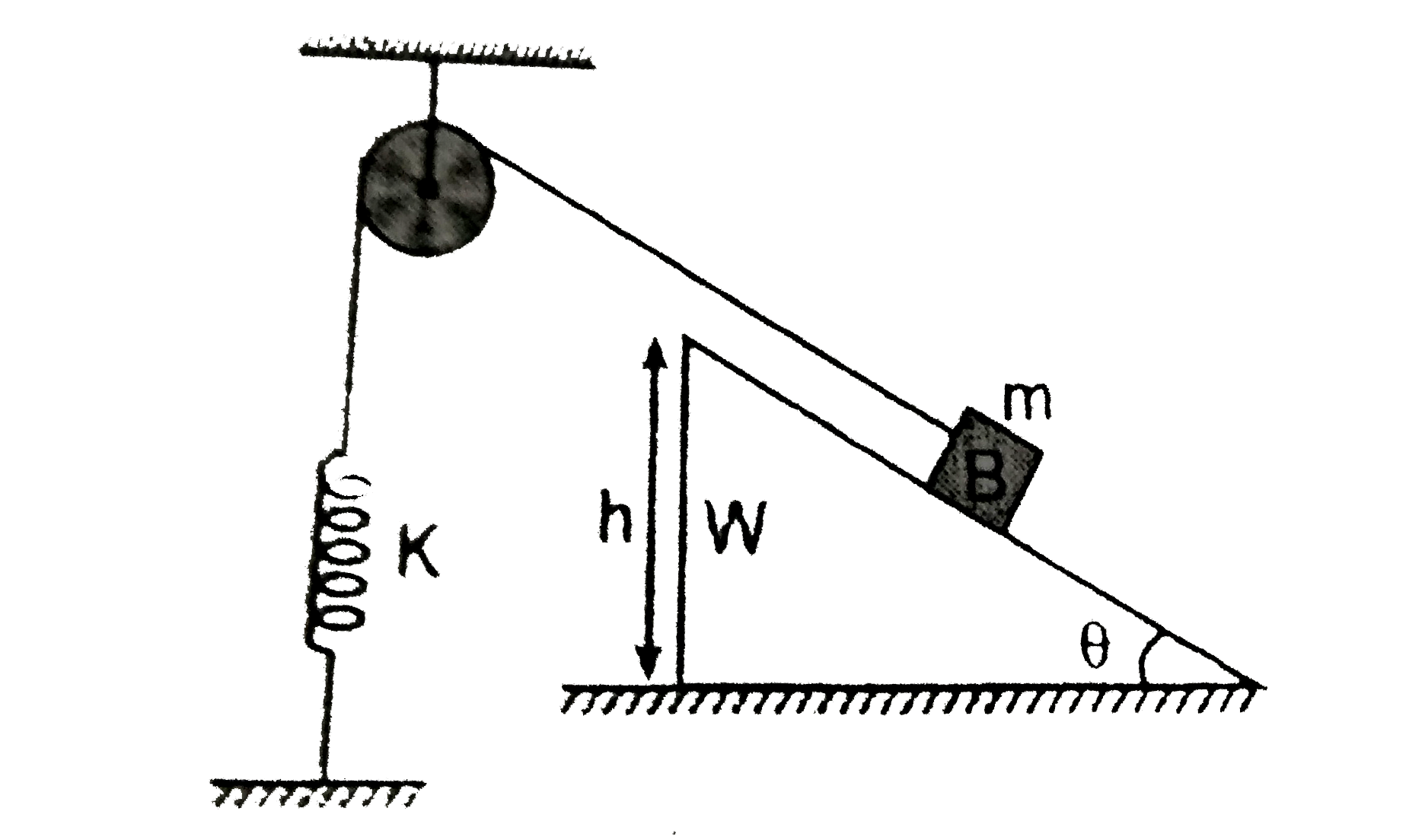
View SolutionThe coefficient of friction between the block and the wedge is μ. Friction between the wedge and the table is to be neglected.
View Solution
Knowledge Check
Calculate angle of friction between wedge and block system is at rest M coefficient of friction between wedge and block.
 Atan−1μB2θCθDθ2
Atan−1μB2θCθDθ2a Block of mass m is placed on a wedge of mass M there is no friction between the block and the wedge .The minmum coefficient of friction between the wedge and the gound so that wedge does not move is,
 Amcos2θM+mcos2θBmsin2θM+mcos2θCmcosθsinθM+mcos2θDmcosθsinθM+msin2θ
Amcos2θM+mcos2θBmsin2θM+mcos2θCmcosθsinθM+mcos2θDmcosθsinθM+msin2θA triangular wedge is placed on smooth horizontal surface. A block is placed on wedge as shown in the figure. Coefficient of friction between block and wedge is μ. Initially system reamins at rest.
 Aμ=tanθBμ=cosθCμ=1tanθDμ=sinθ
Aμ=tanθBμ=cosθCμ=1tanθDμ=sinθ
The coefficient of friction between the wedge and the table is μ. Friction between the block and the wedge is to be neglected.
View SolutionA block lies on a wedge with the slope angle α. The coefficient of static friction between the bar and the wedge is μ<tanα. What should be the acceleration of the wedge to prevent the bar from sliding down?
View SolutionA block of mass m is released from a wedge of mass m as shown in figure . Find the time taken by the block to reach the end of the wedge.
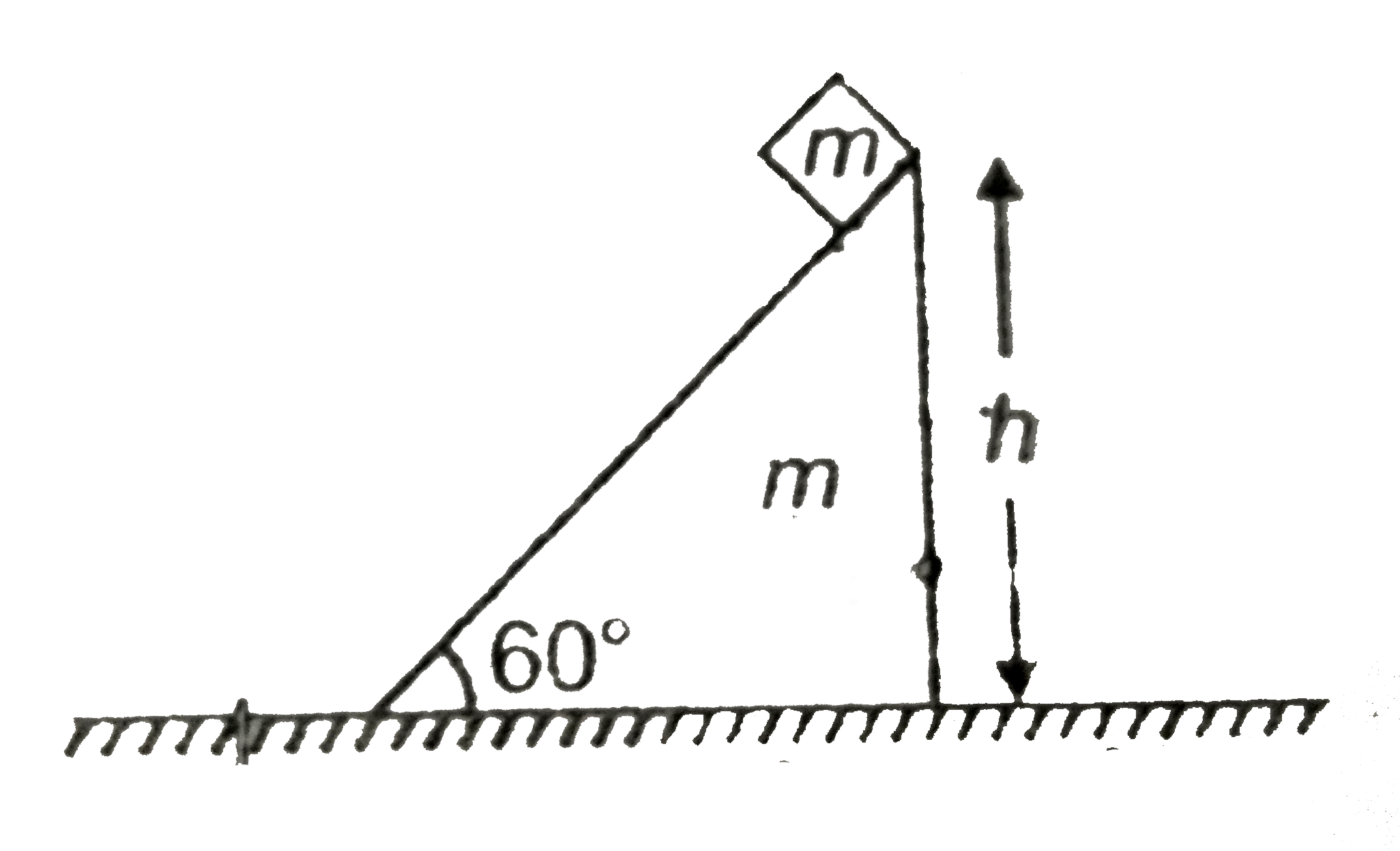
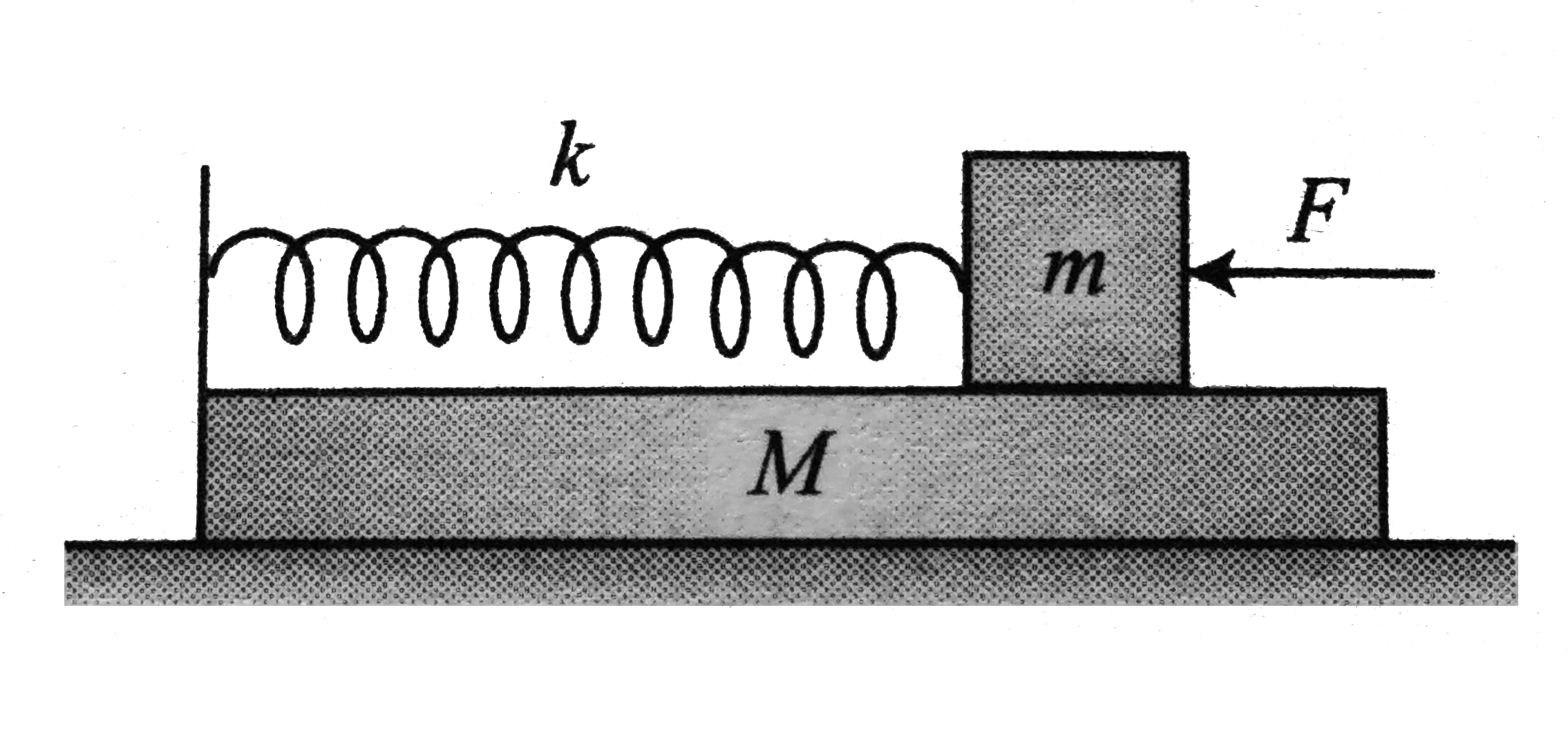
View SolutionA constant force F pushes the block m till the wedge M starts sliding. If the stiffness of the light spring connecting M and m is K, coefficient of friction between block and wedge is μ1 and between the wedge and ground is μ2, find the value of the force F
View SolutionBlock A of mass m and block B of mass 2m are placed on a fixed triangular wedge by means of a light and inextensible string and a frictionless pulley as shown in fig . The wedge is inclined at 45∘ to the horizontal on both sides . The coefficient of friction between the block Aand the wedge is 2/3 and that between the block B and the wedge is 1/3 .If the system of AandB is released from rest then find .
a. the acceleration of A
b. tension in the string
c.the magnitude and direction of the frictional force acting on A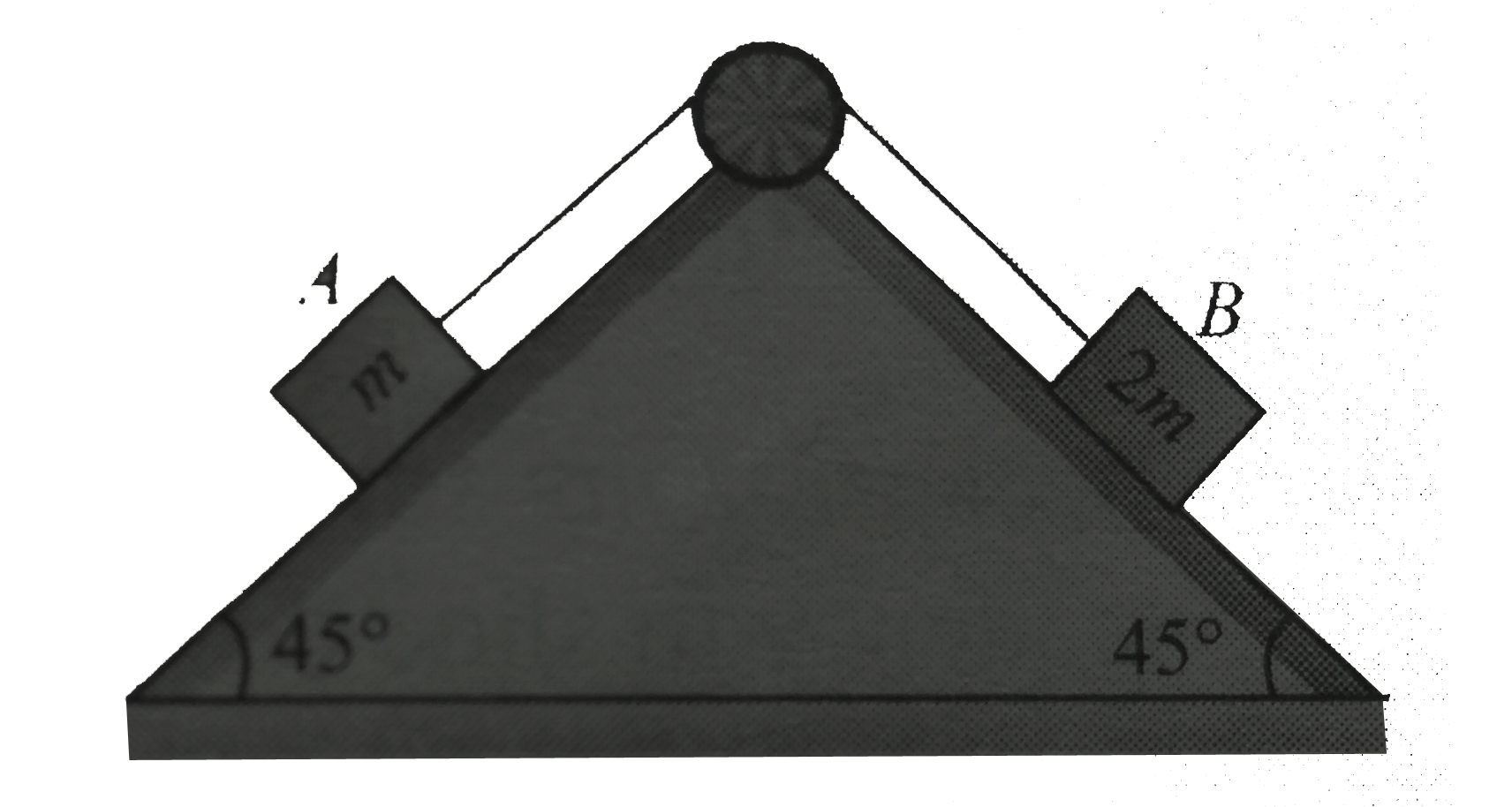
View Solution