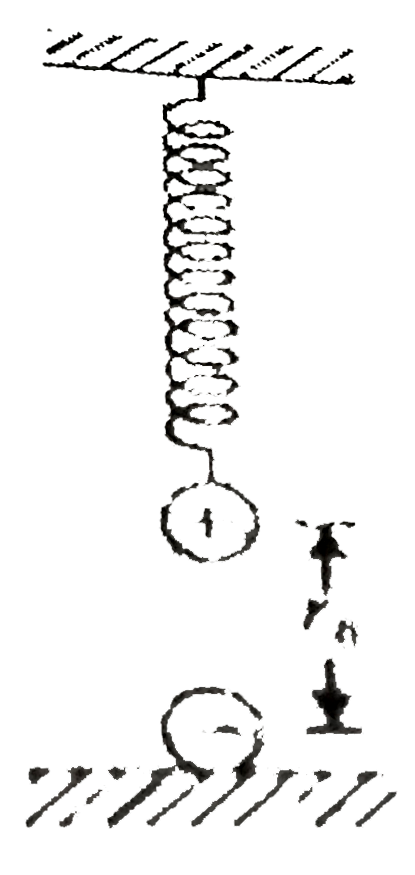
A system consists of two identical cubes, each of mass 3kg, linked together by a compressed weightless spring of force constant 1000Nm−1. The cubes are also connected by a thread which is burnt at a certain moment. At what minimum value of initial compression x0 (in cm) of the spring will the lower cube bounce up after the thread is burnt together?
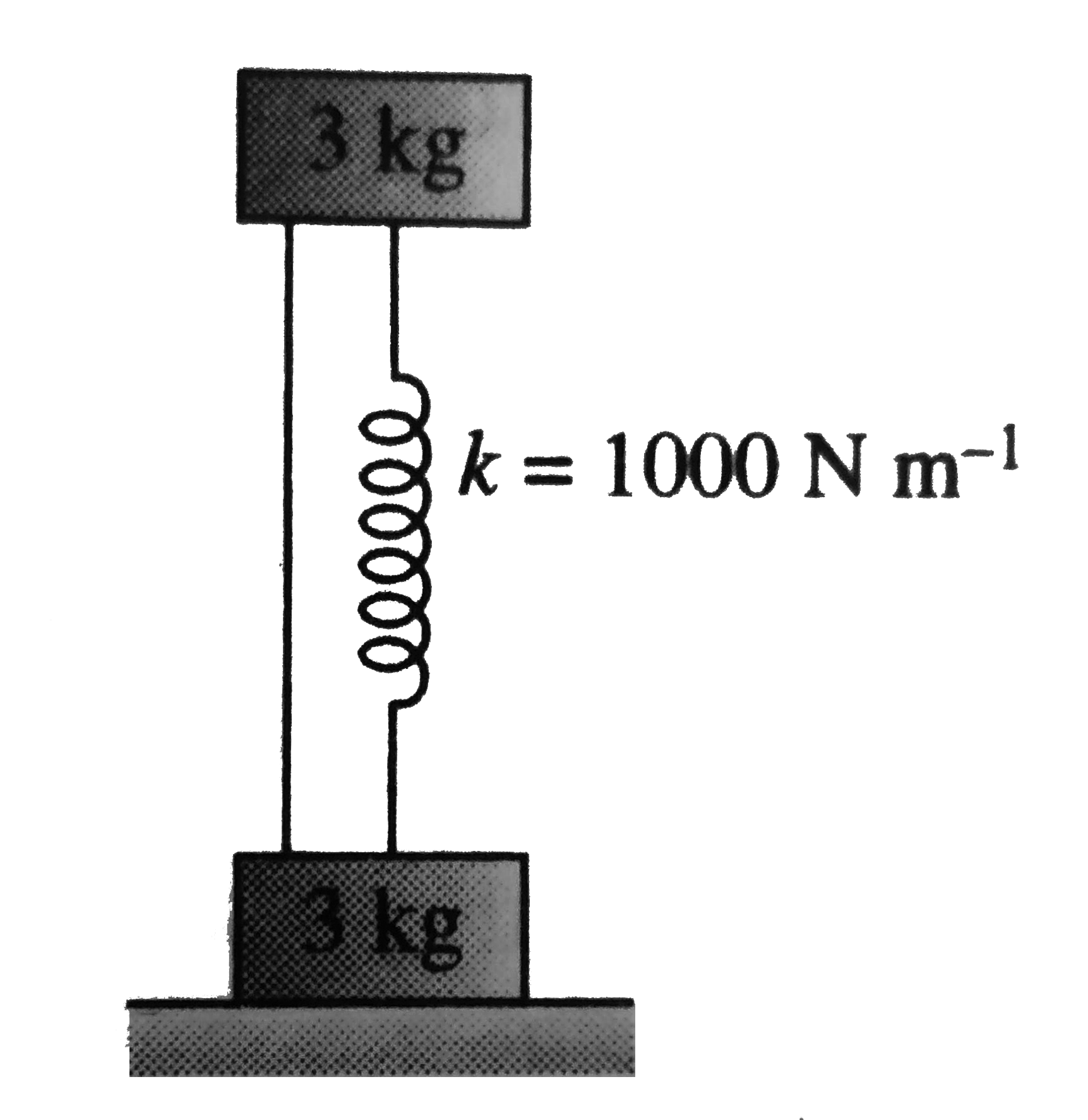
The correct Answer is:9
Let x be the elongation in the spring when it returns back.
12kx20=12kx2+mg(x+x0)
On solving, we get
kx=−mg±(mg−kx0)=−2mg+kx0
(ignoring negative sign) (i)
And also lower block will bounce up if
kx≥mg⇒−2mg+kx0≥mg
So x0=3mgk⇒x0=9cm
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (sinble Correct )19videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives(multiple Correct)3videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension55videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
A system consists of two identical cubes, each of mass m, linked together by the compressed weightless spring of stiffness ϰ (figure). The cubes are also connected by a thread which is burned through at a certain moment. Find:
(a) at what values of Δl, the initial compression of the spring, the lower cube will bounce up after the thread has been burned through:
(b) to what height h the centre of gravity of this system will rise if the initial compression of the spring Δl=7mg/ϰ.
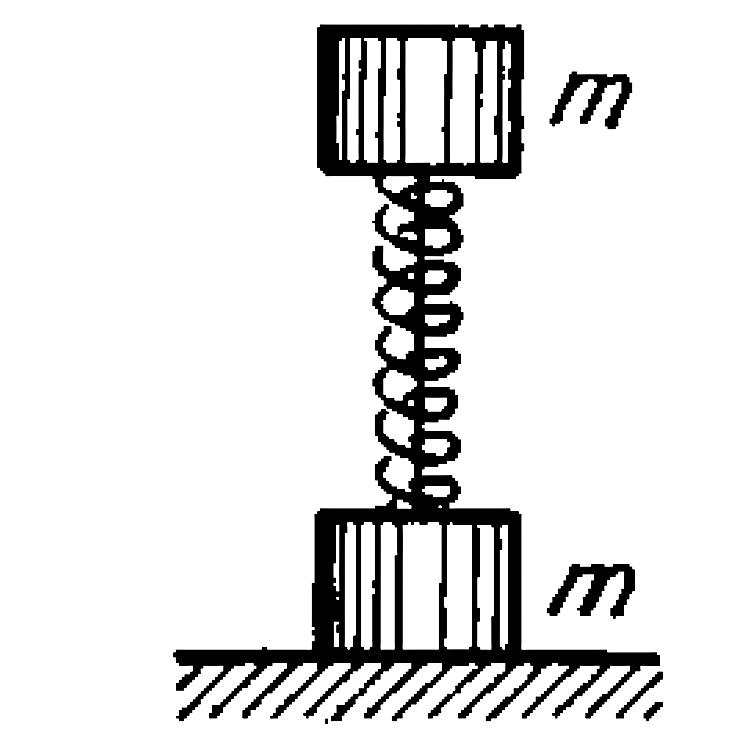 View Solution
View SolutionA system consists of two identical blocks, each of mass m, linked together by the compressed weightless spring of stiffness k, as shown in figure -3.57. The blocks are connected by a thread which is burned through at a certain moment. Find
(a) At what values of initial compression, the inital compression of the spring, the lower block will bounce up after the thread has been burned through
To what height will the centre of gravity of this system will rise if the initial compression of the spring is 7 mg/k
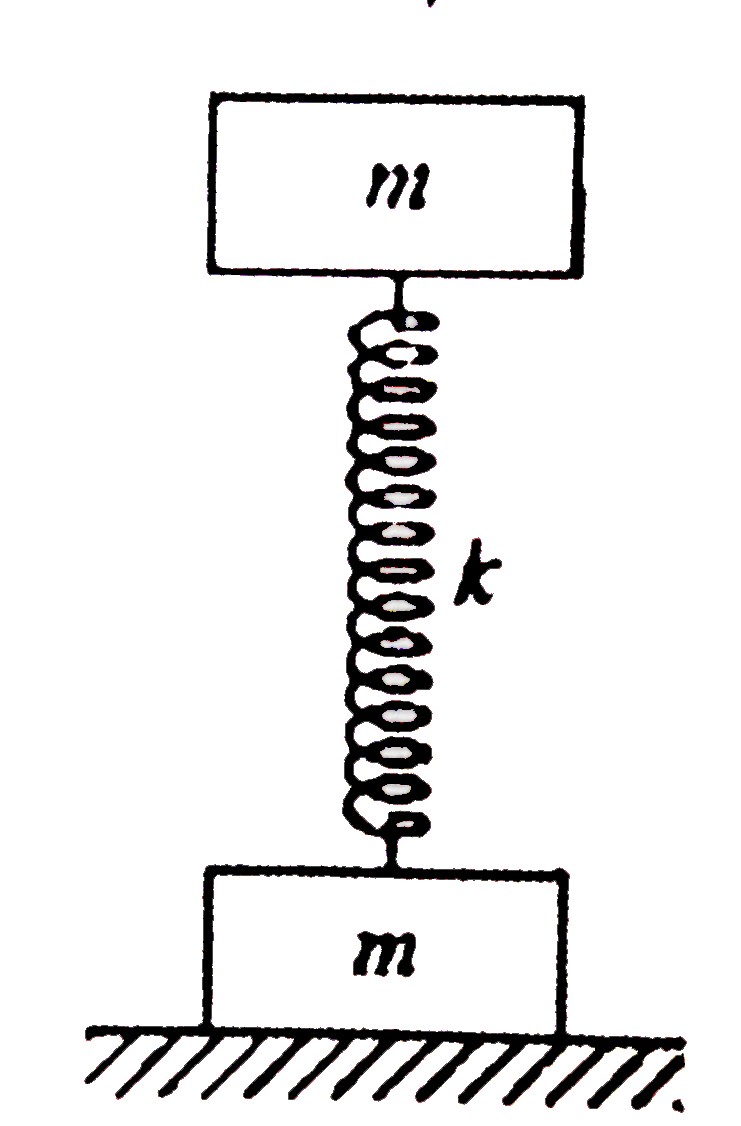 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A system consists of two cubes of mass m1, and m2 respectively connected by a spring of force constant k. force (F) that should be applied to the upper cube for which the lower one just lifts after the force is removed, is
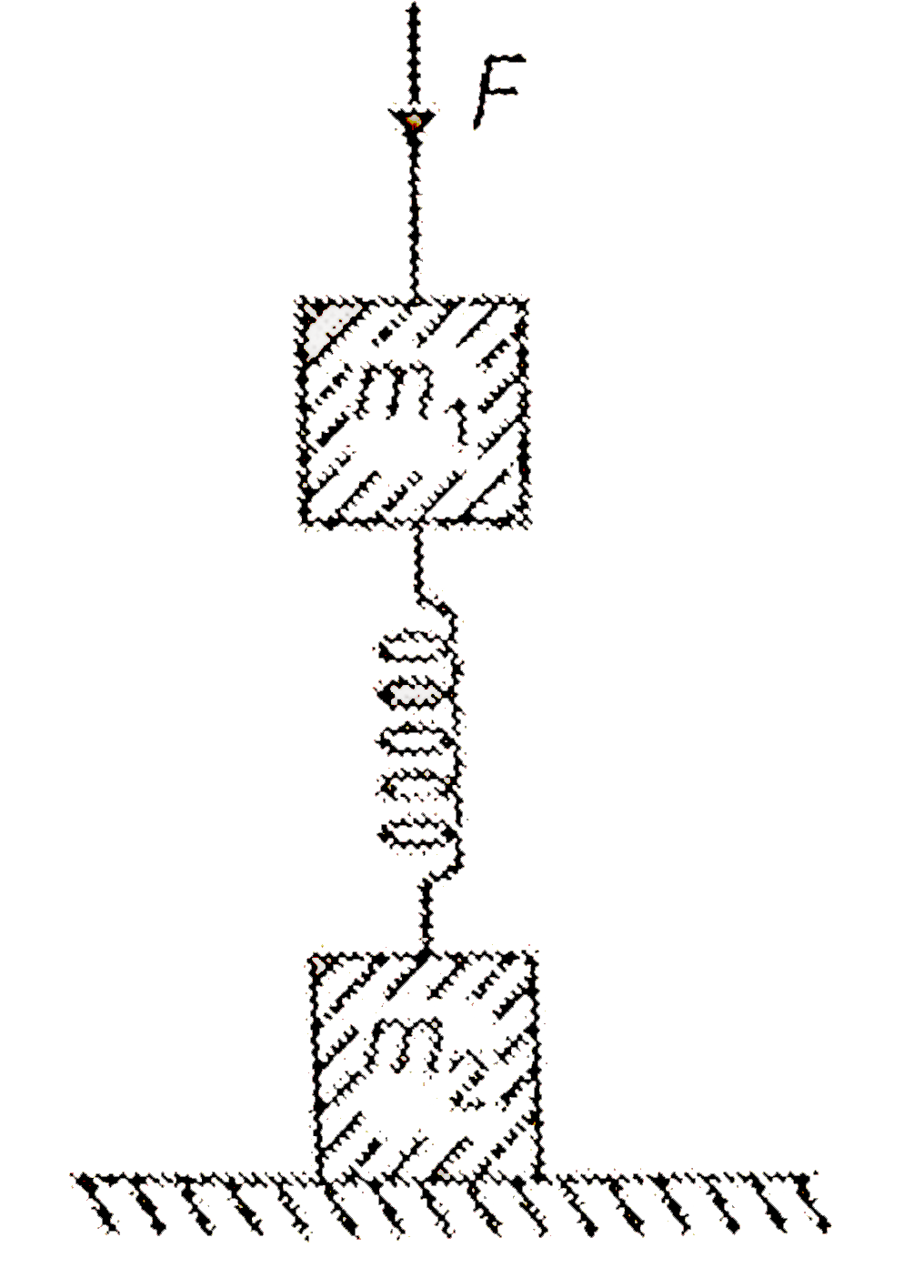 AmgBm2gC(m1+m2)gDm1m2m1+m2g
AmgBm2gC(m1+m2)gDm1m2m1+m2g
A block of mass m=0.14kg is moving with velocity v0 towards a mass less unstretched spring of force constant K=10Nm−1. Coefficient of friction between the block and the ground is μ=1/2.
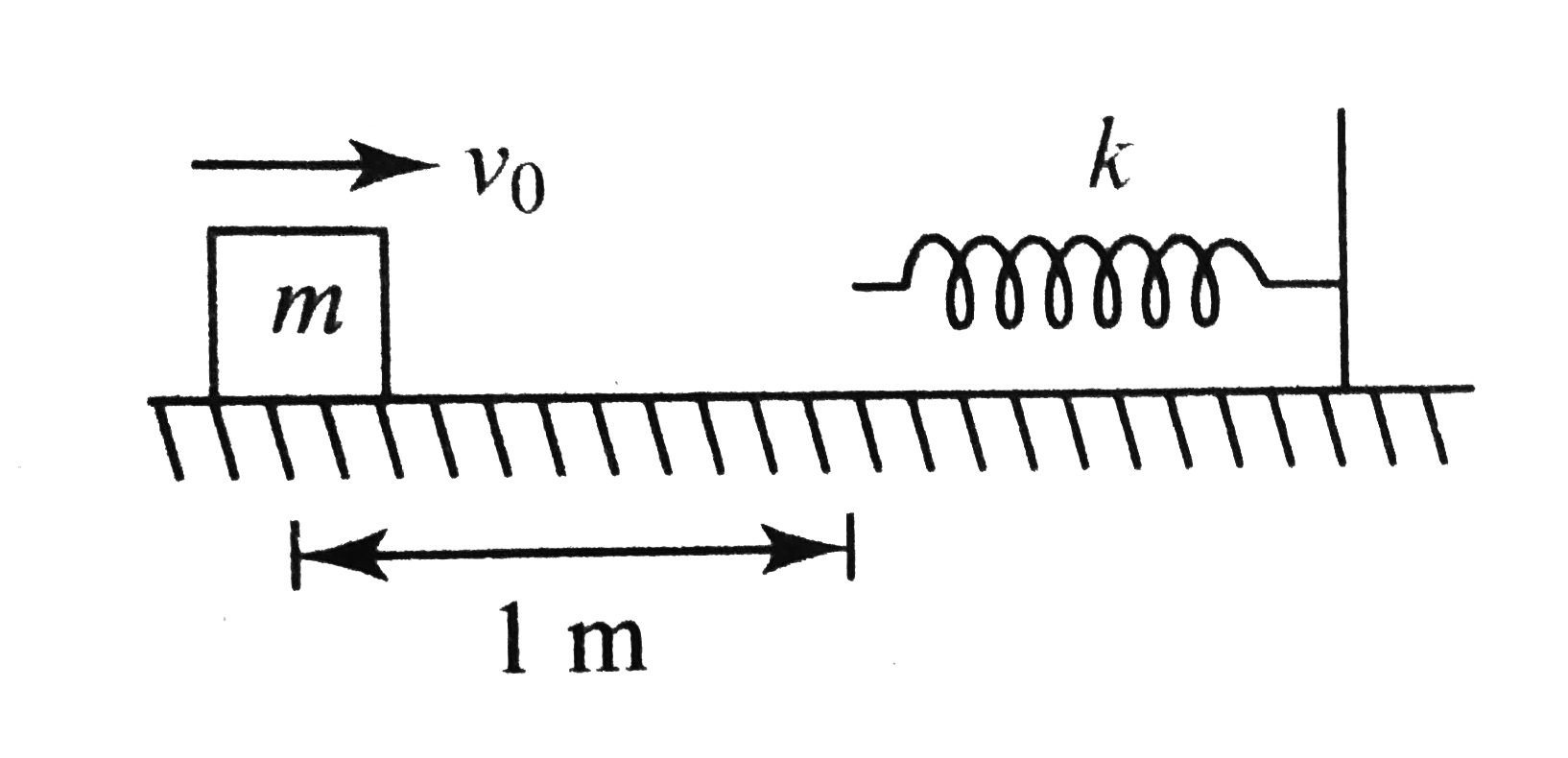
Find the maximum value of compression in the spring (in cm), so that after pressing the spring the block does not return back but stops there permanently.View SolutionTwo blocks of masses m and 2m compress a spring of spring constant k by x0 and blocks are a connected by a thread and placed on a smooth surface as shown. Now , thread is burned. Find the speed of each block when the spring attains its normal length L.
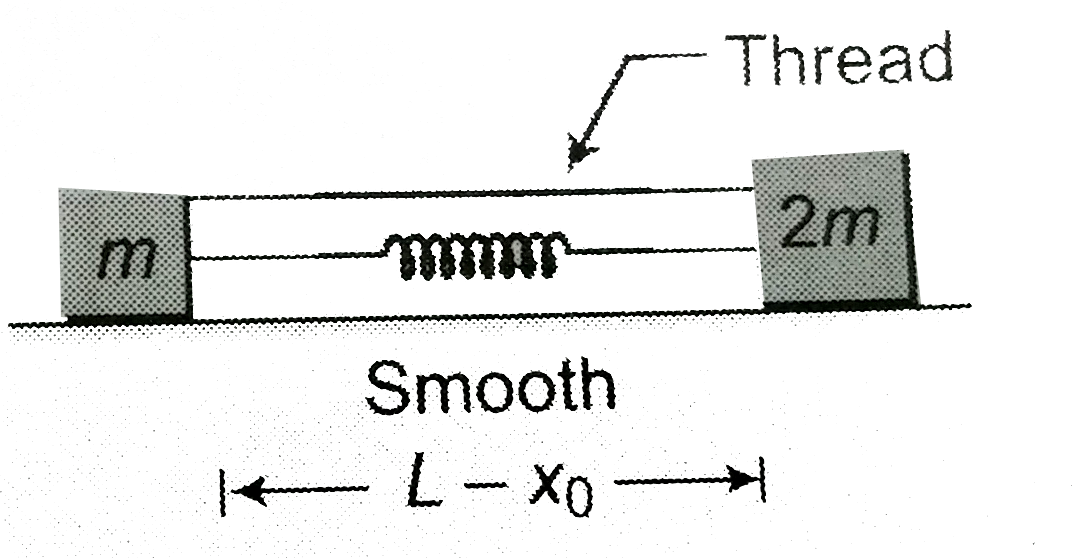 View Solution
View SolutionTwo identical blocks each of mass 1kg are joined together with a compressed spring. When the system is released the two blocks appear to be moving with unequal speeds in the opposite directions as shown in fig.
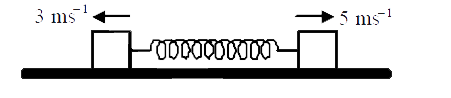
Choose the correct statement -View SolutionTwo identical blocks, each of mass m, are connected through a massless spring of force constant k and arranged as shown in fig the spring is compressed by an amount y by applying an external force and released
(a) What is the velocity of upper block when the spring is relaxed
(b) What should be the initial compression of the spring so that the lower block is just raised above the floor ?
 View Solution
View SolutionA system consists of two small spheres of masses m1 and m2 interconnected by a weightless spring. At the moment t=0 the spheres are set in motion with the initial velocities v1 and v2 after which the system starts moving in the Earth's uniform gravitational field. Neglecting the air drag, find the time dependence of the total momentum of this system in the process of motion and of the radius vector of its centre of inertia relative to the initial position of the centre.
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximu speed of the trolley is
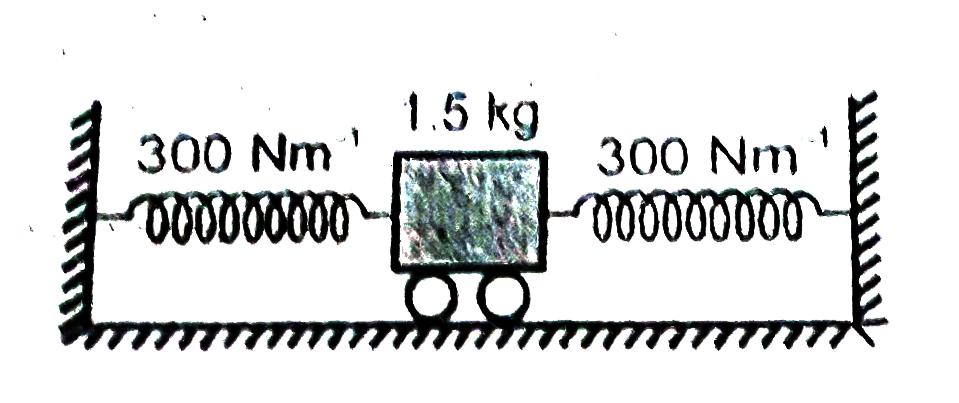 View Solution
View SolutionA positively charged sphere of mass m = 5kg is attached by a spring of force constant K=104 N/m. The sphere is tied with a thread so that spring is in its natural length. Another identical, negatively charged sphere is fixed with floor, vertically below the positively charged sphere as shown in fignre. If initial separation between sphere is r0 = 50cm and magnitnde ofcharge on each sphere is q=100μC, calculate maximum elongation of spring when the thread is burnt. Take g=10m/s2 :
 View Solution
View Solution

