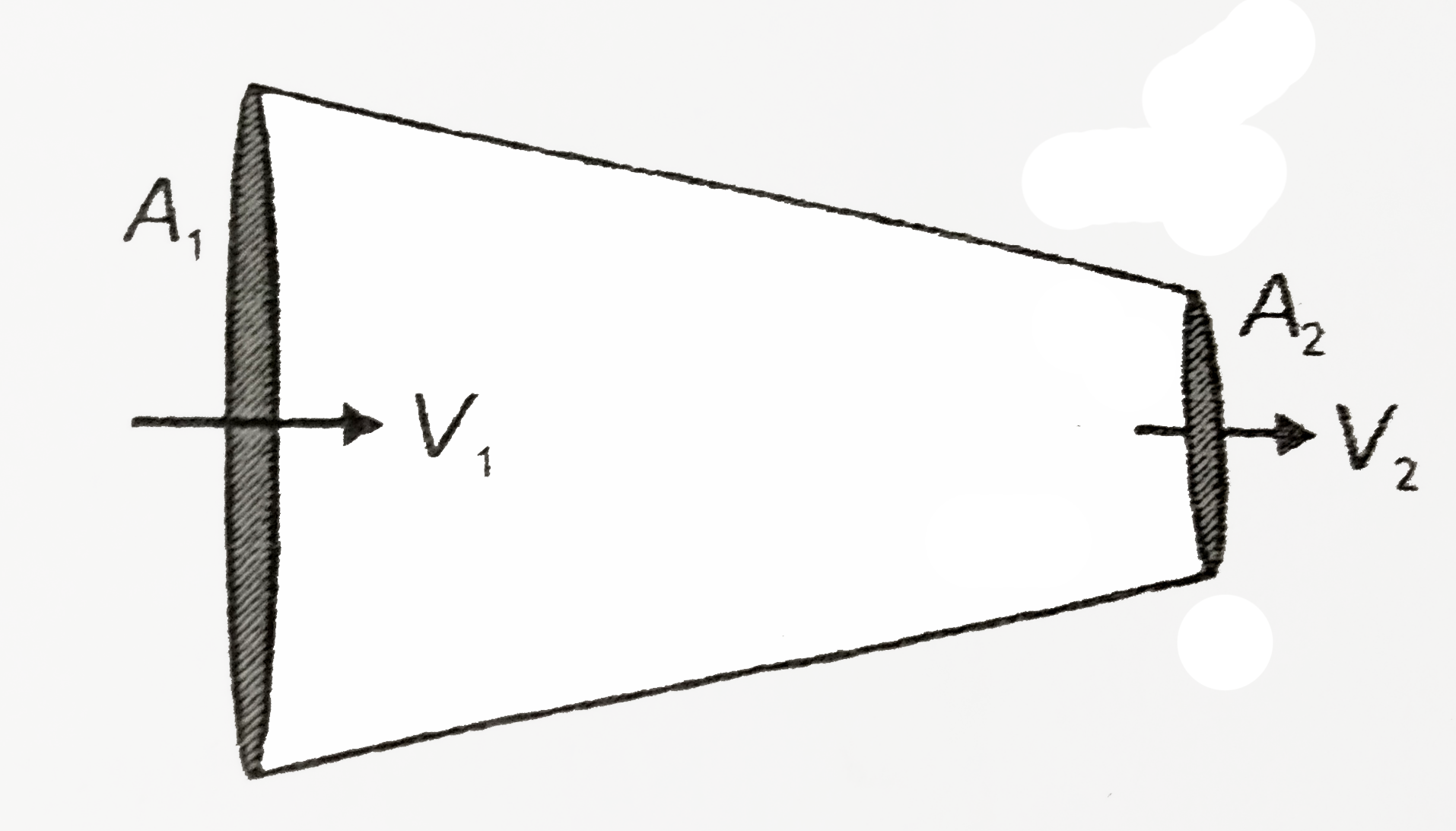
Calculate the rate of flow of glycerine of density 1.25×103kgm−3 through the conical section of a pipe, if the radii of its ends are0.1 m and 0.04 m and the pressure drop across its length is 10Nm−2.
6.43×10−3m3s−1
6.43×10−4m3s−1
6.43×10−4m2s−1
6.43×103m3s−1
The correct Answer is:B
According to continuity equation ,
A1v1=A2v2
or v1v2=A2A1=πr22πr21
=(r2r1)2=(0.040.1)2=425 …(i)
From bernoulli's equation
p1+12ρv21=p2+12ρv22 (Ash1=h2)
or v22−v21=(2p1−p2ρ
or v22−v21=2×101.25×103=1.6×10−2m2s−2 ...(ii)
Solving eqs. (i) and (ii) , we get
v2−0.128ms−1
∴ Rate of volume flow through the tube
Q=A2v2=(πr22)v2=π(0.04)2(0.128)
=6.43×10−4m3s−1

Topper's Solved these Questions
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - FRICTION IN SOLID AND LIQUIDSEXERCISE - EXERCISE 149videos
FRICTION IN SOLID AND LIQUIDS
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - FRICTION IN SOLID AND LIQUIDSEXERCISE - EXERCISE 2 (Miscellaneous Problems)24videos
FRICTION IN SOLID AND LIQUIDS
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - FORCEEXERCISE - Exercise 2 (Miscellaneous Problems)19videos
FORCE
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - GRAVITATION EXERCISE - MHT CET Corner20videos
GRAVITATION
Similar Questions
Calculate the rate of flow of glycerine of density 1.25×103kg/m3 through the conical section of a pipe if the radii of its ends are 0.1m and 0.04 m and the pressure drop across its lengths is 10N/m2.
View SolutionCalculate the rate of flow of glycerine of density 1.20 ×103kg/m3 through the conical section of a pipe. If the radii of its ends are 0.1 m and 0.02 m and the pressure drop across the length is 10 Nm2.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The radii of curvatures of a convex lens are 0.04 m and 0.04m. Its refractive index is 1.5. Its focal length is
A0.04 mB0.4 mC4mD40 m - Question 2 - Select One
A thick rope of rubber of density 1.5×103kgm−3 and Young's modulus 5×106Nm−2, 8 m in length, when hung from ceiling of a room, the increases in length due to its own weight is
A96×10−3mB19.2×10−5mC9.4cmD9.6m - Question 3 - Select One
To what height does a liquid of density 0.4×103 kg m−3 and surface tension 0.05 Nm−1 rise in a capillary tube of radius 0.2 mm when dipped in ? [Given cosθ=0.4g=10ms−2]
A25 cmB15 cmC5 cmD20 cm
Calculate the rate of flow of glycerine of density. 1.25×103kg/m3 through the conical section of a pipe. If the radii of its ends are 1.0m and 0.04m and the pressure drop across its length is 10N/m2.
View SolutionCalculate the moment of inertia of a cylinder of length 1.5m, radius 0.05m and density 8×103kg/m3 about the axis of the cylinder.
View SolutionIn the figure shown below, a fluid of density 2×103 kg m−3 is flowing in a horizontal pipe. The speed of water at point A is 4 cm s−1, what is its speed at point B?
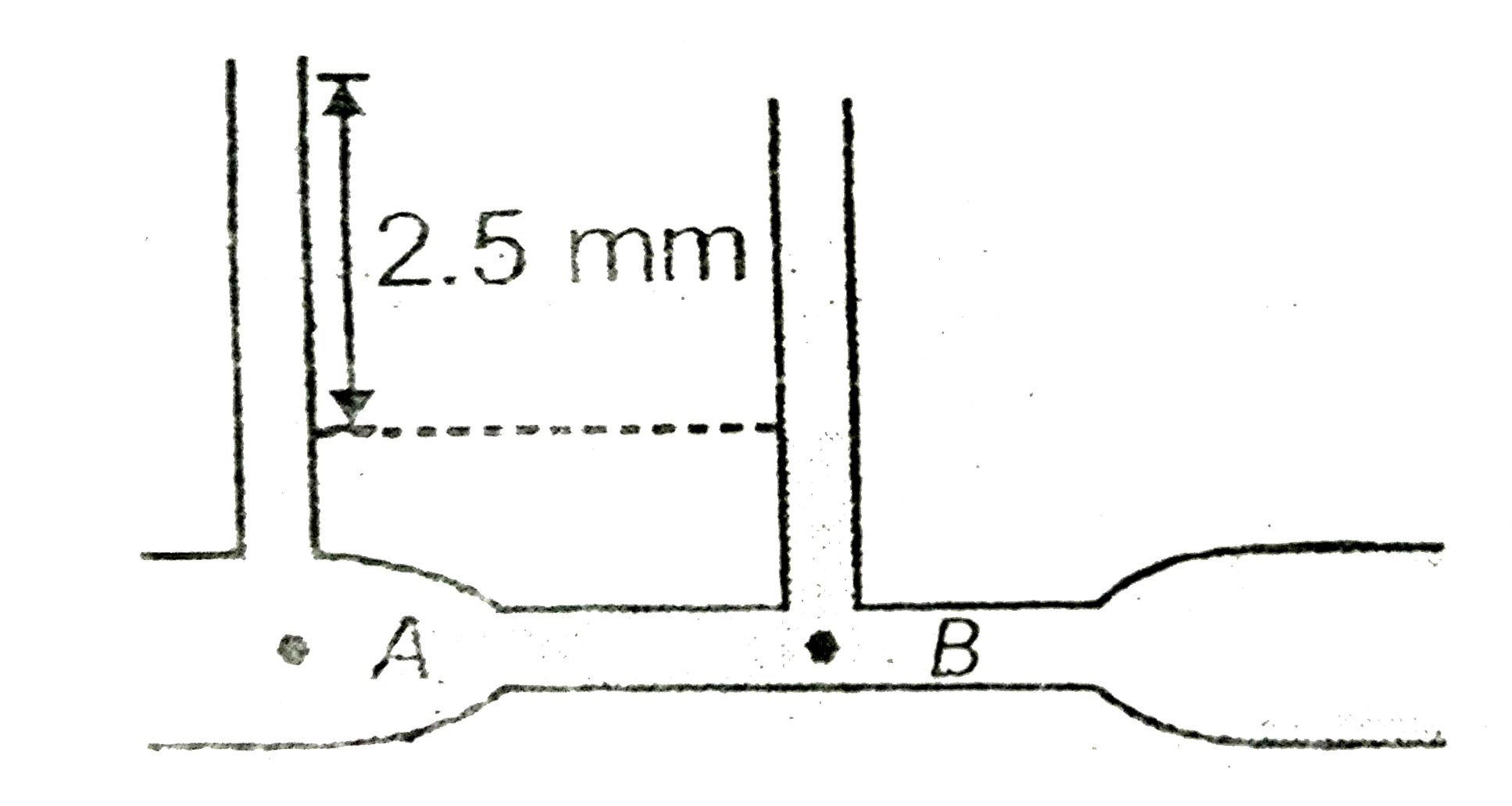 View Solution
View SolutionCalculate the rate of flow (volume per second) of a liquid through a capillary tube of diameter 0.20×10−3m and length 1m,η=3.00×10−5Nm−2s and pressure gradient = 10 atm.
View SolutionA conductor of mass 0.50 kg and density 9×103kgm−3 has a resistance of 0.015Ω . Calculate the length of the conductor if its shape is cylindrical and the resistivity of its material is 1.8×10−7Ωm.
View Solution

