Calculate the rate of flow (volume per second) of a liquid through a capillary tube of diameter 0.20×10−3m and length 1m,η=3.00×10−5Nm−2s and pressure gradient = 10 atm.
r=0.2×10−32=0.1×10−3m
=10−4m,p=10atm=10×1.01×105Pa
=1.01×106Pa
We have,
η=πpr4t8VI
∴ rate of flow =Vt=πpr48ηl
=(22/7)×(1.01×106)(10−4)48×(3.0×10−3)×1
=1.32×10−8m5s−1
Topper's Solved these Questions
- SOLID AND LIQUID STATES BOOK - RC MUKHERJEECHAPTER - SOLID AND LIQUID STATES EXERCISE - PROBLMES (ANSWERS BRACKTED WITH QUESTIONS)
38 Videos
- SOLID AND LIQUID STATES BOOK - RC MUKHERJEECHAPTER - SOLID AND LIQUID STATES EXERCISE - OBJECTIVE PROBLEMS
51 Videos
- PROPERTIES OF GASESBOOK - RC MUKHERJEECHAPTER - PROPERTIES OF GASESEXERCISE - OBJECTIVE PROBLEMS
5 Videos
- VOLUMETRIC CALCULATIONS BOOK - RC MUKHERJEECHAPTER - VOLUMETRIC CALCULATIONS EXERCISE - OBJECTIVE PROBLEMS
37 Videos
Similar Questions
A capillary tube of length 5 cm and diameter 1 mm is connected to a tank horizontally. The rate of flow of water is 10 ce per minute. Calculate the rate of flow of water through another capillary tube of diameter 2 mm and length 50 cm is connected in series with the first capillary?
View SolutionUnder a constant pressure head, the rate of streamlined volume flow of a liquid through a capillary tube is V. if the length of the capillary tube is double and diameter of the bore is halved, find the rate of flow of the liquid through the capillary tube.
View Solution
Knowledge Check
Under a constant pressure head, the rate of flow of orderly volume flow of liquid through a capillary tube is V. IF the length of the capillary is doubled and the diameter of the bore is halved, the rate of flow would become
AV/4B16 VCV/8DV/32Water is conveyed through a uniform tube of 8 cm in diameter and 3140 m in length at the rate 2×10−3m3 per second. The pressure required to maintain the flow is ( viscosity of water =10−3 )
A1. 6.25×103Nm−2B2. 0.625Nm−2C3. 0.0625Nm−2D4. 0.00625Nm−2Water is conveyed throuh a uniform tube of 8 cm in diameter and 3140 m in length at the rate 2×10−3m3 per second. The pressure required to maintain the flow is ( viscosity of water =10−3 )
A6.25×103Nm−2B0.625Nm−2C0.0625Nm−2D0.00625Nm−2
Calculate the rate of flow of glycerine of density 1.20 ×103kg/m3 through the conical section of a pipe. If the radii of its ends are 0.1 m and 0.02 m and the pressure drop across the length is 10 Nm2.
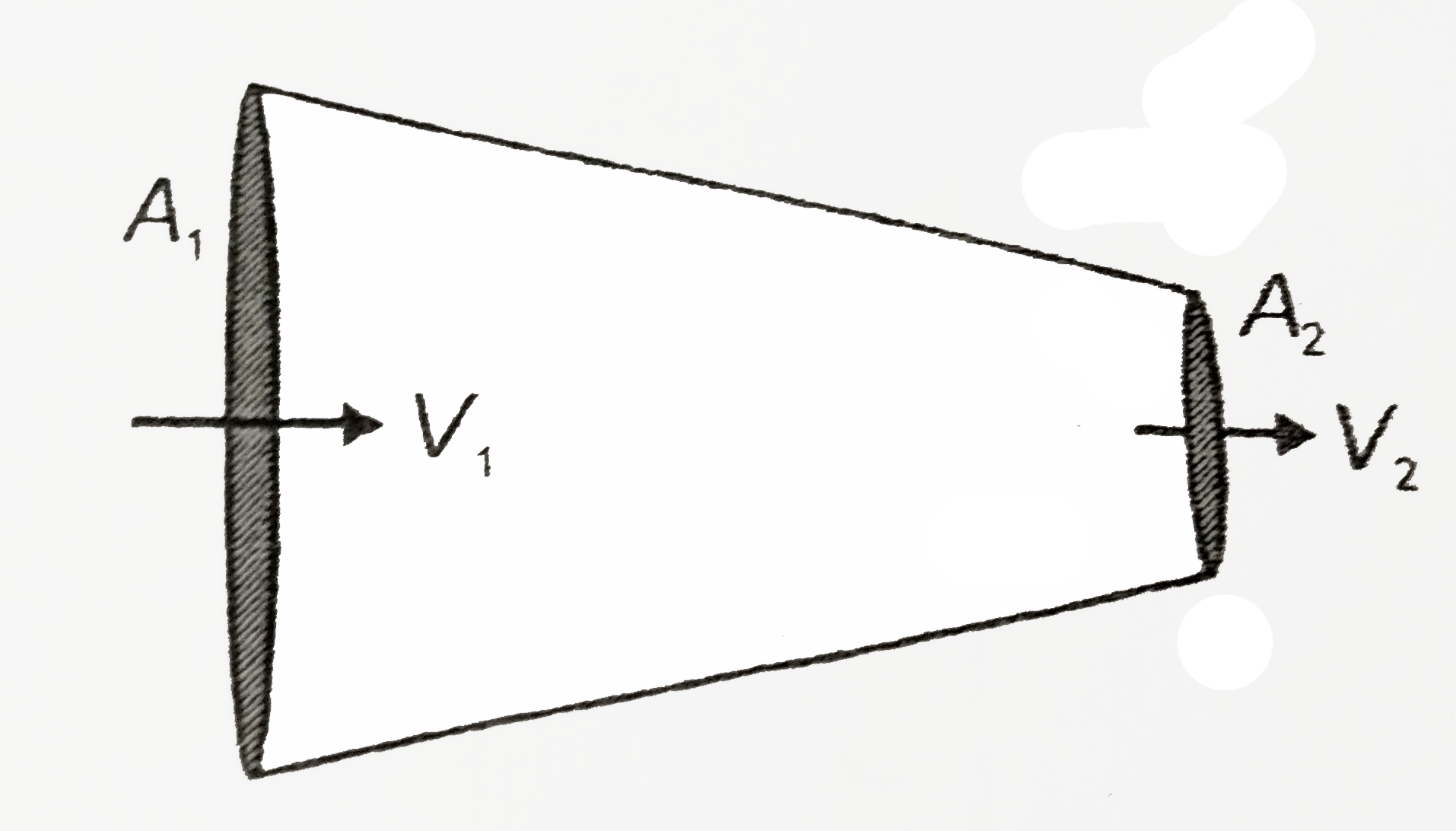
View SolutionCalculate the rate of flow of glycerine of density 1.20 ×103kg/m3 through the conical section of a pipe. If the radii of its ends are 0.1 m and 0.02 m and the pressure drop across the length is 10 Nm2.

View SolutionCalculate the rate of flow of glycerine of density 1.25×103kgm−3 through the conical section of a pipe, if the radii of its ends are0.1 m and 0.04 m and the pressure drop across its length is 10Nm−2.
View SolutionCalculate the rate of flow of glycerine of density 1.25×103kgm−3 through the conical section of a pipe, if the radii of its ends are0.1 m and 0.04 m and the pressure drop across its length is 10Nm−2.
View SolutionThe lower end of a capillary tube of diameter 2.0 mm is dipped 8.00cm below the surface of water in a beaker. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water? The surface tension of water at temperature of the experiments is 7.30×10−2Nm−1. 1 atmospheric pressure =1.01×105Pa, density of water =1000kg/m3,g=9.80ms−2. also calculate the excess pressure.
View Solution
