The water level on a tank is 5m high. There is a hole of 1cm2 cross-section at the bottom of the tank. Find the initial rate with which water will leak through the hole. (g=10ms−2)
10−3m3s−1
10−4m3s−1
10m3s−1
10−2m3s−1
The correct Answer is:A
Rate of leakage of water from the hole
=Av=A√2gh
=10−4√2×10×5=10−3m3s−1
Topper's Solved these Questions
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - FRICTION IN SOLID AND LIQUIDSEXERCISE - EXERCISE 2 (Miscellaneous Problems)24videos
FRICTION IN SOLID AND LIQUIDS
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - FRICTION IN SOLID AND LIQUIDSEXERCISE - EXERCISE 2 (Miscellaneous Problems)24videos
FRICTION IN SOLID AND LIQUIDS
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - FORCEEXERCISE - Exercise 2 (Miscellaneous Problems)19videos
FORCE
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - GRAVITATION EXERCISE - MHT CET Corner20videos
GRAVITATION
Similar Questions
The level of water in a huge tank is 20 m. Nearly at the bottom of the tank, there is a hole of 2 cm? cross section. The rate with which the water will leak through the hole is n×10−3cm. Find the value of n.
View SolutionThe level of water in a tank is 5m high.A hole of area 1cm^2 is made in the bottom of the tank. The rate of leakage of water from the hole is (g=10ms^(-2)
View Solution
Knowledge Check
- Question 1 - Select One
The level of water in a tank is 5 m high. A hole of area of cross section 1 cm2 is made at the bottom of the tank. The rate of leakage of water for the hole in m3s−1 is (g=10ms−2)
A10−3B10−4C10D10−2 - Question 2 - Select One
The level of water in a tank is 5 m high . A hole of the area 10cm2 is made in the bottom of the tank . The rate of leakage of water from the hole is
A10−2m3s−1B102m3s−1C10m3s−1D10−4m3s−1 - Question 3 - Select One
A tank of height 5 m/s completely filled with water. There is a hole of cross sectional area 1cm2 near its bottom. What is the initial volume of water that will come out of the hole per second. (Use g=10m/s2)
A10−3m3/sB2×10−3m3/sC3×10−2m3/sD4×10−3m3/s
A cylindrical tank of cross sectional area a1 is filled with water to a height h. A hole of cross sectional area a2 is made at the bottom. If a1=5a2, then find the
(i) initial velocity with which the water falls in tank.
(ii) initial velocity with which water emerges out from hole.
(iii) time taken to make the tank empty.View SolutionA water tank is placed on a platform of height 5 m high and there is an orifice near the bottom in the wall of tank at 5 m below the level of water. Find the speed with which water will hit the ground [Take g = 10 m/s2 ]
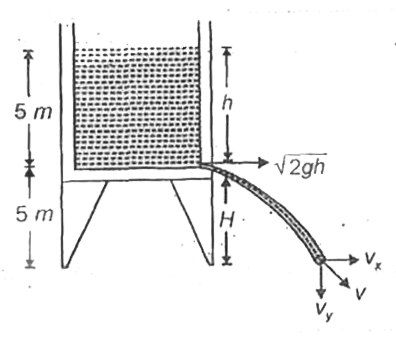 View Solution
View SolutionA tank of large base area is filled with water up to a height of 5m. A hole of 2cm2 cross section in the bottom allows the water to drain out in continuous streams. For this situation, mark out the correct statement(s) (take ρwater=1000kg/m3,g=10ms−12)
 View Solution
View SolutionA cylindrical tank is filled with water to a level of 3m. A hole is opened at a height of 52.5 cm from bottom. The ratio of the area of the hole to that of cross-sectional area of the cylinder is 0.1. The square of the speed with which water is coming out from the orifice is (Take g=10m/s2)
View SolutionA cylindrical tank having cross-sectional area A is filled with water to a height of 2.0 m. A circular hole of corss-section area is opened at a height of 75 cm from the bottom. If a/A=√0.2, then velocity with which waer emerges from the hole is
(g=9.8ms−2)View Solution

