A cylindrical tank is filled with water to a level of 3m. A hole is opened at a height of 52.5 cm from bottom. The ratio of the area of the hole to that of cross-sectional area of the cylinder is 0.1. The square of the speed with which water is coming out from the orifice is (Take g=10m/s2)
50m2/s2
40m2/s2
51.5m2/s2
50.5m2/s2
The correct Answer is:C
To find the square of the speed with which water is coming out from the orifice of the cylindrical tank, we can use Torricelli's theorem, which states that the speed v of efflux of a fluid under the force of gravity through an orifice is given by:
v=√2gh
where:
- g is the acceleration due to gravity,
- h is the height of the water column above the hole.
Step 1: Determine the height h of the water column above the hole.
The total height of the water in the tank is 3 m, and the hole is located at a height of 52.5 cm (or 0.525 m) from the bottom. Therefore, the height h of the water column above the hole is:
h=3m−0.525m=2.475m
Step 2: Substitute the values into the equation for speed v.
Now we can substitute h into the equation for v:
v=√2gh=√2×10m/s2×2.475m
Step 3: Calculate v2.
We need to find v2:
v2=2gh=2×10×2.475
Calculating this gives:
v2=20×2.475=49.5m2/s2
Step 4: Adjust for the area ratio.
The problem states that the ratio of the area of the hole A1 to the cross-sectional area of the cylinder A2 is given as 0.1. Therefore, we need to adjust the speed using the formula:
v2=2gh1−A21A22
Given that A1A2=0.1, we have:
A21A22=(0.1)2=0.01
Thus, we can substitute this into our equation:
v2=49.51−0.01=49.50.99
Calculating this gives:
v2≈50.0m2/s2
Final Answer:
The square of the speed with which water is coming out from the orifice is approximately:
50.0m2/s2
- g is the acceleration due to gravity,
- h is the height of the water column above the hole.
The total height of the water in the tank is 3 m, and the hole is located at a height of 52.5 cm (or 0.525 m) from the bottom. Therefore, the height h of the water column above the hole is:
Now we can substitute h into the equation for v:
We need to find v2:
The problem states that the ratio of the area of the hole A1 to the cross-sectional area of the cylinder A2 is given as 0.1. Therefore, we need to adjust the speed using the formula:
The square of the speed with which water is coming out from the orifice is approximately:
Topper's Solved these Questions
- BOOK - MTG GUIDECHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Check Your Neet Vitals22videos
PROPERTIES OF BULK MATTER
- BOOK - MTG GUIDECHAPTER - PROPERTIES OF BULK MATTEREXERCISE - AIPMT/NEET (MCQs)40videos
PROPERTIES OF BULK MATTER
- BOOK - MTG GUIDECHAPTER - PROPERTIES OF BULK MATTEREXERCISE - AIPMT/NEET (MCQs)40videos
PROPERTIES OF BULK MATTER
- BOOK - MTG GUIDECHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - AIPMT / NEET MCQ14videos
PHYSICAL WORLD AND MEASUREMENT
- BOOK - MTG GUIDECHAPTER - THERMODYNAMICSEXERCISE - AIPMT/NEET (MCQs)26videos
THERMODYNAMICS
Similar Questions
Water is filled in a cylindrical container to a height of 3m. The ratio of the cross-sectional area of the orifice and the beaker is 0.1. The square of the speed of the liquid coming out from the orifice is (g=10m/s2).
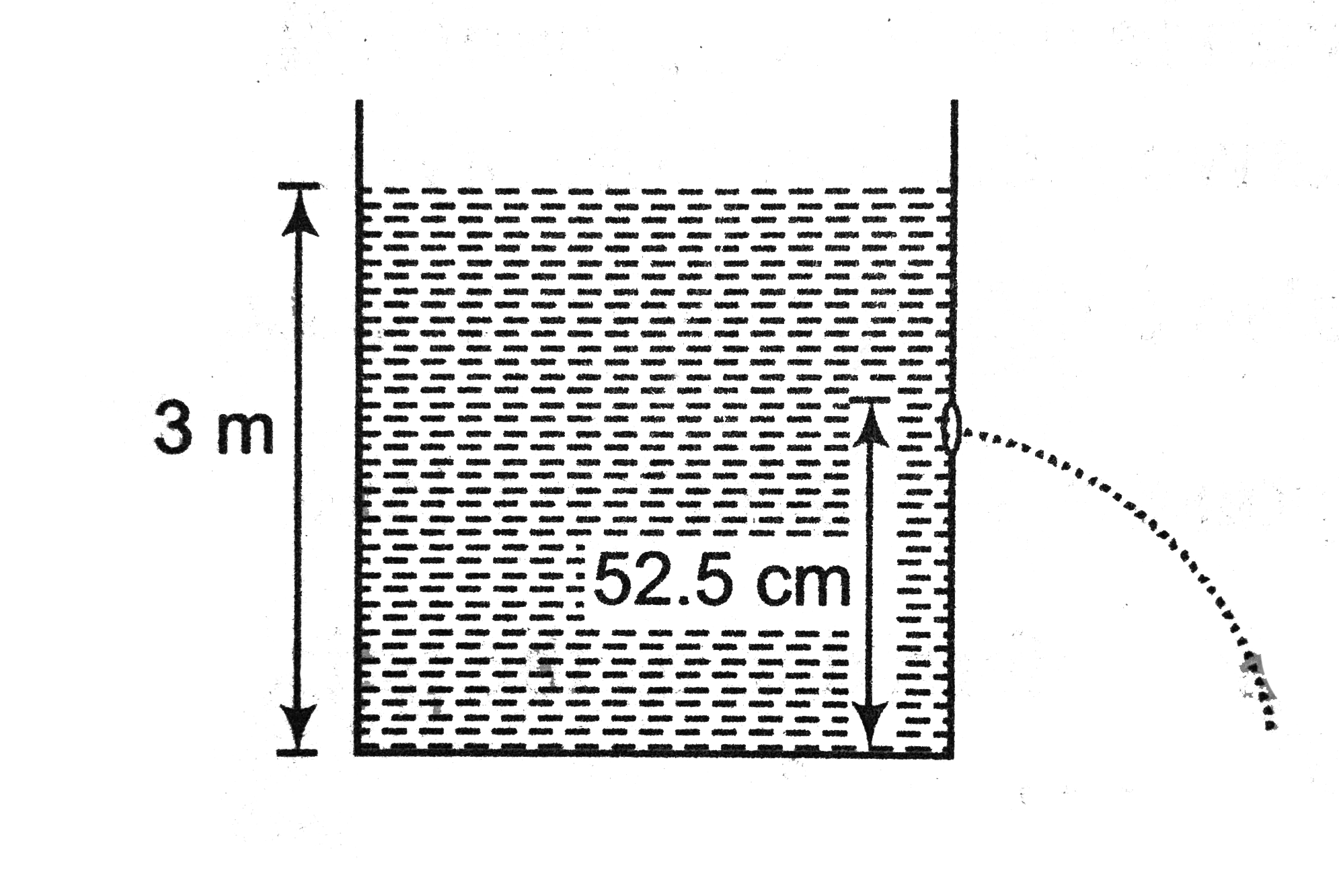 View Solution
View SolutionThe water level on a tank is 5m high. There is a hole of 1cm2 cross-section at the bottom of the tank. Find the initial rate with which water will leak through the hole. (g=10ms−2)
View Solution
Knowledge Check
- Question 1 - Select One
A cylindrical tank is filled with water to a level of 4 m. A hole is opened at a height of 60 cm from bottom. The ratio of the area of the hole to that at cross-sectinal area at cylinder is 0.2. Then the velocity with which water is coming out is (g=10m/s2)
A7.9m/sB9.2m/sC8.4m/sD8.9m/s - Question 2 - Select One
What is filled in a cylindrical container to a height of 3m. The ratio of the cross-sectional area of the orifice and the beaker is 0.1. The square of the speed of the liquid coming out from the orifice is (g=10m/s2).
A50m2/s2B50.5m2/s2C51m2/s2D52m2/s2 - Question 3 - Select One
Water is filled in a cylindrical container to a height of 3m. The ratio of the cross-sectional area of the orifice and the beaker is 0.1. The square of the speed of the liquid coming out from the orifice is (g=10m/s2).
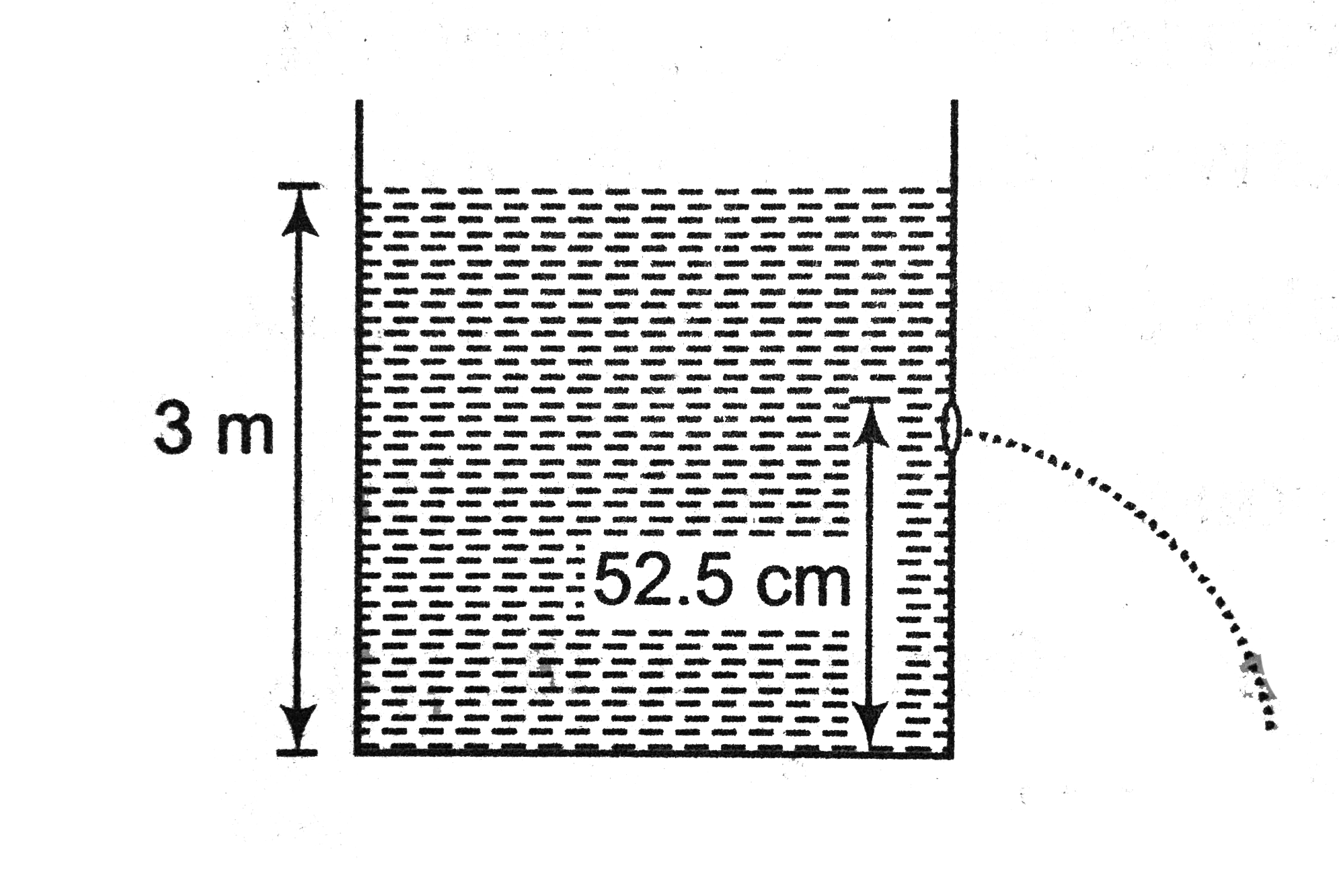 A50m2/s2B50.5m2/s2C51m2/s2D52m2/s2
A50m2/s2B50.5m2/s2C51m2/s2D52m2/s2
Water is filled in a container upto height 3m. A small hole of area 'a' is punched in the wall of the container at a height 52.5 cm from the bottom. The cross sectional area of the container is A. If a/A=0.1 then v2 is (where v is the velocity of water coming out of the hole)
View SolutionA large tank filled with water to a height h is to be emptied through a small hole at the bottom. The ratio of times taken for the level of water to fall from h to h2 and from h2 to zero is
View SolutionAt the mount of the tap area of cross-section is 2.0cm2 and the speed of water is 3m/s. The area of cross-section of the water column 80 cm below the tap is (use g=10m/s2)
View SolutionWater is filled to height h in a fixed vertical cylinder placed on horizontal surface. At time t=0 a small hole a drilled at a height h/4 from bottom of cylinder as shown. The cross section area of hole is a and the cross-section area of cylinder is A such that A>>a.

The duration of time for which water flows out of hole is.View SolutionA cylindrical tank having cross-sectional area A is filled with water to a height of 2.0 m. A circular hole of corss-section area is opened at a height of 75 cm from the bottom. If a/A=√0.2, then velocity with which waer emerges from the hole is
(g=9.8ms−2)View Solution

