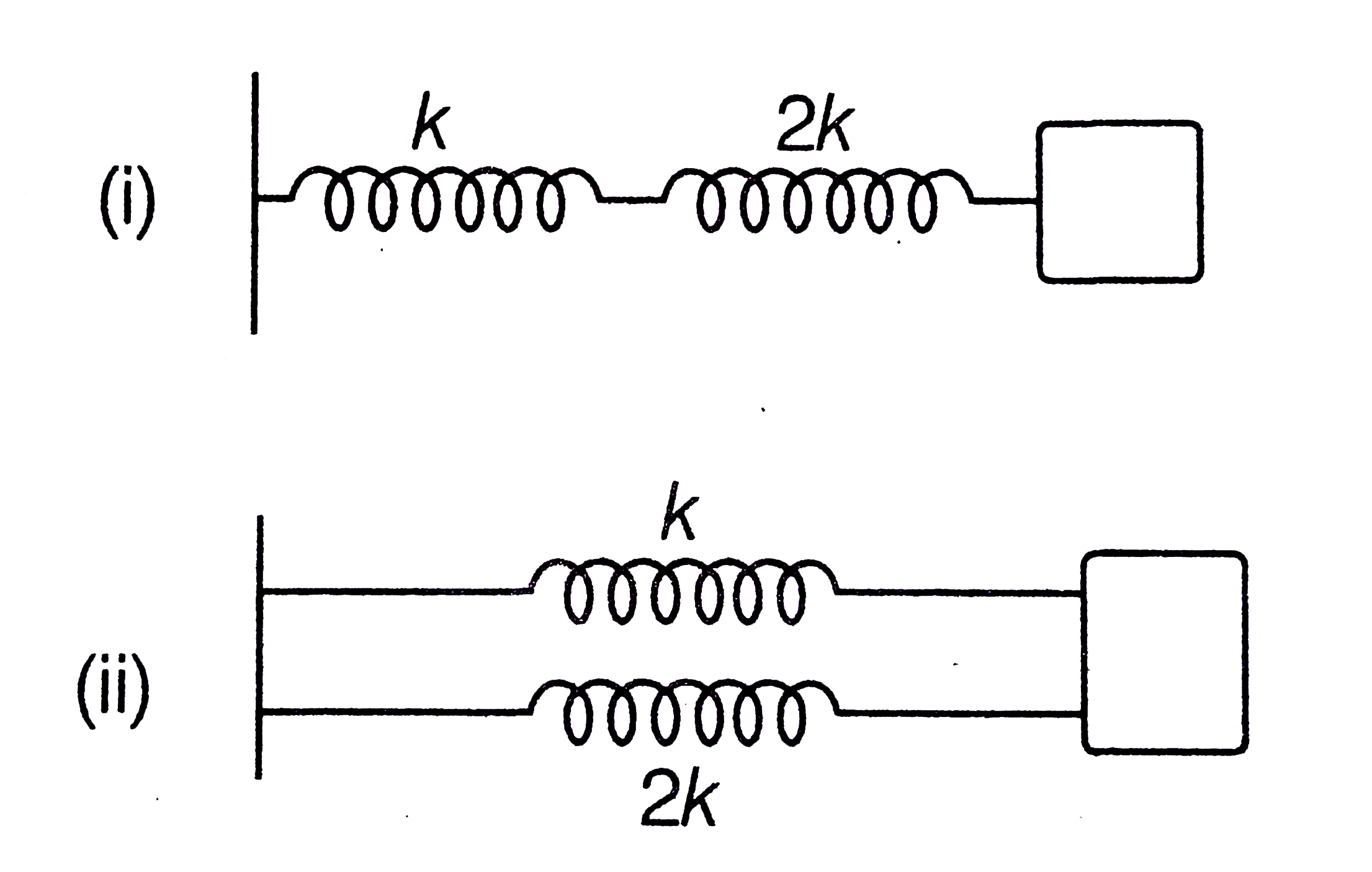
If ksandkp, respectively are effective spring constants in series and parallel combination of springs as shown in the figure, find kskp
92
37
29
73
The correct Answer is:C
In the arrangement shown in Fig (i) the two springs are in series. The effective spring constant ks of this
1ks=1k+12k=2+12k=32k [∵ks=2k3]
In the arrangement shown in Fig. (ii) the two springs are in parallel. The effective spring constant kp of this arrangement is
kp=k1+k2=k+2k=3k
Thus, kskp=2k/33k=29
Topper's Solved these Questions
- OSCILLATIONSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - OSCILLATIONSEXERCISE - EXERCISE 2
49 Videos
- OSCILLATIONSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - OSCILLATIONSEXERCISE - MHT CET CORNER
29 Videos
- OSCILLATIONSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - OSCILLATIONSEXERCISE - MHT CET CORNER
29 Videos
- MOCK TEST 5BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MOCK TEST 5EXERCISE - MCQs
42 Videos
- PRACTICE SET 01BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PRACTICE SET 01EXERCISE - PAPER 1 (PHYSICS & CHEMISTRY)
50 Videos
Similar Questions
Knowledge Check
If ks and kp respectively are effective spring constant in series and parallel combination of springs as shown in figure, find kskp.
 A92B37C29D73
A92B37C29D73If ks and kp respectively are effective spring constant in series and parallel combination of springs as shown in figure, find kskp.
 A92B37C29D73
A92B37C29D73Two spring of spring constant k1 and k2 are joined in series The effective spring constant of the combination is given by
A√k1k2B(k1+k2)/2Ck1+k2Dk1k2k1+k2
Two springs of spring constantsK1 and K2 are joined in series. The effective spring constant of the combination is given by
View SolutionTwo spring of spring constants k1 and k2 ar joined and are connected to a mass m as shown in the figure. Calculate the frequency of oscillation of mass m.

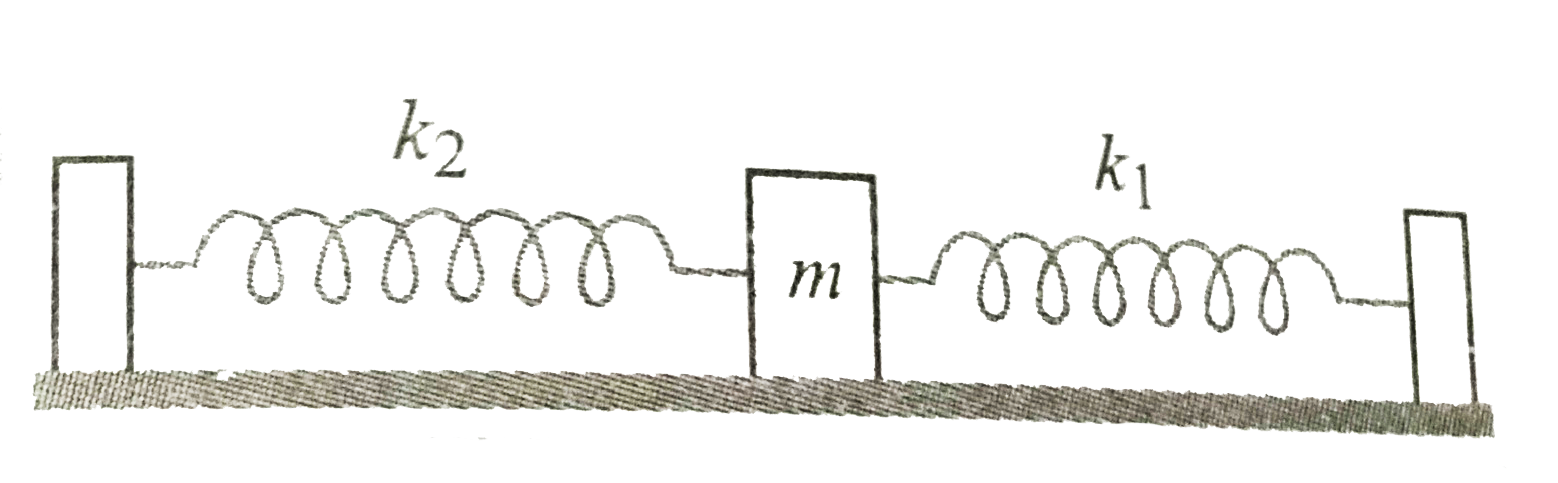
View SolutionTwo spring have force constants k1 and k2 respectively. They are attached to a mass m and two fixed supports as shwon in figure. If the surface is frictionless, fing the time period of oscillations. What is the spring factore of this combination.
View SolutionTwo springs of spring constantsK1 and K2 are joined in series. The effective spring constant of the combination is given by
View SolutionA mass is suspended separately by two springs of spring constants k1 and k2 in successive order. The time periods of oscillations in the two cases are T1 and T2 respectively. If the same mass be suspended by connecting the two springs in parallel, (as shown in figure) then the time period of oscillations is T. The correct relations is

View Solution
