Two springs of spring constants and are joined in series. The effective spring constant of the combination is given by
The correct Answer is:C
To find the effective spring constant of two springs joined in series, we can follow these steps:
Step 1: Understand the System
When two springs with spring constants K1 and K2 are connected in series, the total elongation d of the system is the sum of the elongations x and y of each spring:
d=x+y
Step 2: Apply Hooke's Law
According to Hooke's Law, the force exerted by a spring is proportional to its elongation:
F=kx
For the first spring:
F1=K1x
For the second spring:
F2=K2y
Step 3: Relate Forces
Since both springs are in series and the same force F acts on both, we have:
F1=F2=F
Thus, we can write:
F=K1x=K2y
Step 4: Express Elongations in Terms of Force
From the equations above, we can express the elongations x and y in terms of the force F:
x=FK1
y=FK2
Step 5: Substitute Elongations into Total Elongation
Substituting x and y into the total elongation equation gives:
d=FK1+FK2
Step 6: Factor Out the Force
Factoring out F from the right side, we get:
d=F(1K1+1K2)
Step 7: Define Effective Spring Constant
The effective spring constant Keq is defined by the relationship:
F=Keqd
Substituting for d:
F=Keq(F(1K1+1K2))
Step 8: Solve for Effective Spring Constant
Dividing both sides by F (assuming F≠0):
1=Keq(1K1+1K2)
Thus, we can express Keq:
Keq=1(1K1+1K2)
Step 9: Simplify the Expression
This can be simplified to:
Keq=K1K2K1+K2
Final Answer
The effective spring constant of the combination of springs in series is:
Keq=K1K2K1+K2
When two springs with spring constants K1 and K2 are connected in series, the total elongation d of the system is the sum of the elongations x and y of each spring:
d=x+y
According to Hooke's Law, the force exerted by a spring is proportional to its elongation:
F=kx
For the first spring:
F1=K1x
For the second spring:
F2=K2y
Since both springs are in series and the same force F acts on both, we have:
F1=F2=F
Thus, we can write:
F=K1x=K2y
From the equations above, we can express the elongations x and y in terms of the force F:
x=FK1
y=FK2
Substituting x and y into the total elongation equation gives:
d=FK1+FK2
Factoring out F from the right side, we get:
d=F(1K1+1K2)
The effective spring constant Keq is defined by the relationship:
F=Keqd
Substituting for d:
F=Keq(F(1K1+1K2))
Dividing both sides by F (assuming F≠0):
1=Keq(1K1+1K2)
Thus, we can express Keq:
Keq=1(1K1+1K2)
This can be simplified to:
Keq=K1K2K1+K2
The effective spring constant of the combination of springs in series is:
Keq=K1K2K1+K2
Similar Questions
What is the spring constant for the combination of shown in figure ?
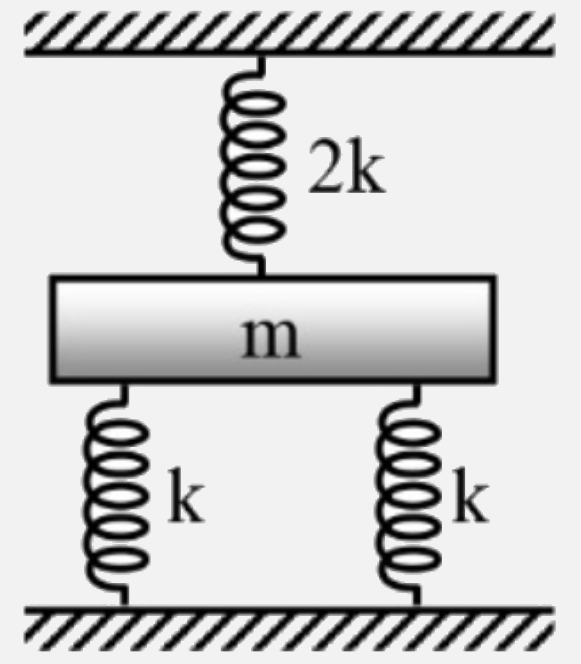 View Solution
View SolutionTwo springs, of spring constants k1 and K2, have equal highest velocities, when executing SHM. Then, the ratio of their amplitudes (given their masses are in the ratio 1:2) will be
View SolutionA mass is suspended separately by two springs of spring constants k1 and k2 in successive order. The time periods of oscillations in the two cases are T1 and T2 respectively. If the same mass be suspended by connecting the two springs in parallel, (as shown in figure) then the time period of oscillations is T. The correct relations is
 View Solution
View SolutionInfinite springs with force constantk , 2k, 4k and 8 k .... respectively are connected in series. The effective force constant of the spring will b
View SolutionA light spring of spring constant k is cut into two equal halves. Each half is connected in parallel then net spring constant of the combination is :
View SolutionA spring of spring constant k is cut in three equal pieces. The spring constant of each part will be
View SolutionThe effective spring constant of two spring system as shown in figure will be
 View Solution
View SolutionAs shown in the figure, two light springs of force constant k1 and k2 oscillate a block of mass m. Its effective force constant will be
 View Solution
View SolutionThe electrical analog of a spring constant k is
View SolutionInfinite springs with force constants k,2k, 4k and 8k … respectively are connected in series. What will be the effective force constant of springs, when k=10N/m
View Solution

