A uniform rod of length (L) and area of cross-section (A) is subjected to tensil load (F). If σ be the Poisson's ratio and Y be the Young's modulus of the material of the rod, then find the volumetric strain produced in the rod.
5AY(L+2σ)
FAY(L−2σ)
zero
None of these
Young's modulus i.e., Y=stressStrain=F/AΔ/L
∴ΔLL=FAY
Now, by definition of poisson's ratio
σ=Lateral strainLongitudinal strain=−Δr/rΔL/L
By using Eq. (i) , Δrr=−σ.ΔLL=−σFAY
Now, ΔVV=2Δrr+ΔLL
by using Eqs. (i) and (ii) we get
⇒ΔVV=2(−σFAY)+FAY
=FAY(1−2σ)
Topper's Solved these Questions
- ELASTICITY Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:ELASTICITY Exercise:EXERCISE 1
Explore 66 Videos
- ELASTICITY Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:ELASTICITY Exercise:EXERCISE 2
Explore 48 Videos
- CURRENT ELECTRICITYBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:CURRENT ELECTRICITYExercise:MHT CET CORNER
Explore 32 Videos
- ELECTROMAGNETIC INDUCTIONBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:ELECTROMAGNETIC INDUCTIONExercise:MHT CET CONER
Explore 34 Videos
Similar Questions
A uniform bar of length 2 m and cross-sectional area 50cm2 is subjected to a tensile load 100 N. If Young's modulus of material of bar is 2×107N/m2 and poisson's ratio is 0.4, then determine the volumetric strain.
View SolutionA uniform rod of length L and mass M is pulled horizontally on a smooth surface with a force F. Determine the elongation of rod if Young's modulus of the material is Y.
View Solution
Knowledge Check
A wire of length L and area of cross-section A, is stretched by a load. The elongation produced in the wire is I. If Y is the Young's modulus of the material of the wire, then the torce corstant of the wire is
AYLABYlACYALDYAlA unifrom bar of Length 'L' and cross sectional area 'A' is subjected to a tesnile load 'F','Y' be the Young's modulus and 'σ' be the Poisson's ratio then volumeteric strain is
AFAY(1−σ)BFAY(2−σ)CFAY(1−2σ)DFAYσA unifrom steel rod of length 1m and area of cross-section 20cm2 is hanging from a fixed support. Find the increases in the length of the rod.
A1.923×10−5cmB2.923×10−5cmC1.123×10−5cmD3.123×10−5cm
A metallic wire of length L, area of cross-section A is suspended by attaching some wieght to it. If α is the longitudinal strain and Y is Young's modulus, find the ratio between elastic potential energy and the elastic energy density.
View SolutionA uniform rod of length 2L, area of cross - section A and Young's modulus Y is lying at rest under the action of three forces as shown.
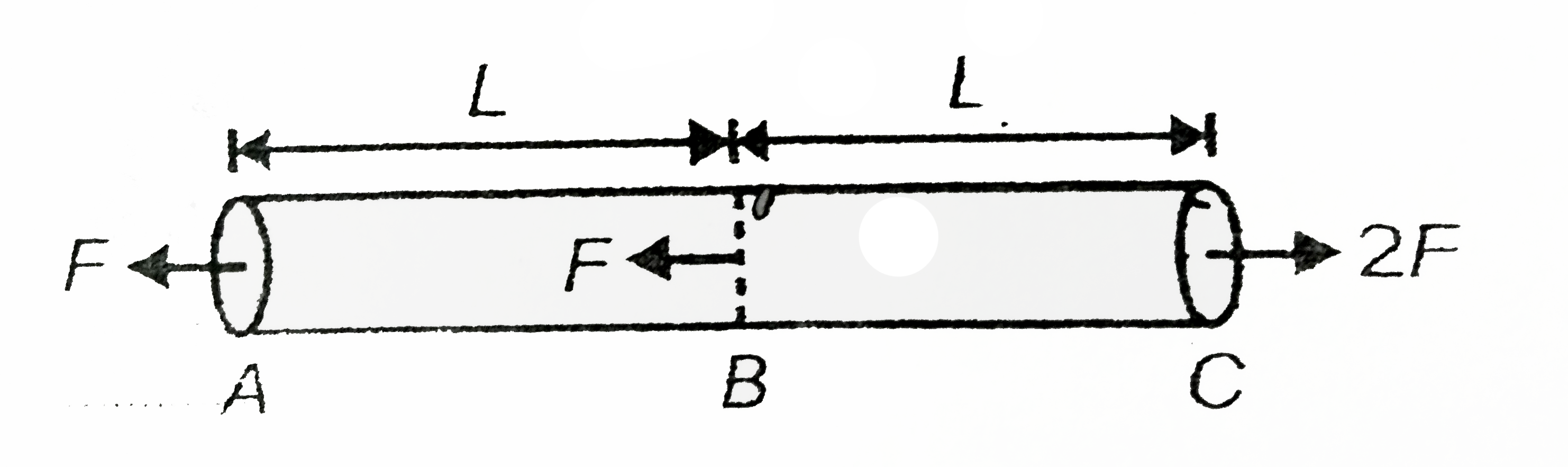
Select the correct alternatives.
View SolutionThe increase in energy of a metal bar of length L and cross-sectional area A when compressed with a load M along its length is (where, Y= Young's modulus of the material of metal bar)
View SolutionAn iron rod of length 2 m and cross-sectional area of 50mm2 is stretched by 0.5 mm, when a mass of 250 Kg is hung from its lower end. Young's modulus of iron rod is
View SolutionAn iron rod of length 2m and cross section area of 50mm2, stretched by 0.5 mm, when a mass 250 kg is hung from its lower end. Young's modulus of the iron rod is
View Solution