TLA,TSA and TSL be the value of surface tension at liquid-air, solid air and solid-liquid interface, respectively. Match the following columns.

A-1, B-2, C-3
A-2, B-3, C-1
A-1, B-3, C-2
A-3, B-1, C-2
The correct Answer is:A
According to the concept of surface tension,
(A) When TSA>TSL,θ will be the in between 0∘ to 90∘.
(B) When TSA<TSL,θ lies between 90∘ to 180∘.
(C) When TSL+TLAcosθ>TSA, molecules of liquid will not be in equilibrium.
Topper's Solved these Questions
- SURFACE TENSION BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SURFACE TENSION EXERCISE - Exercise 2 (Miscellaneous Problems)
42 Videos
- SURFACE TENSION BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SURFACE TENSION EXERCISE - MHT CET Corner
15 Videos
- SURFACE TENSION BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SURFACE TENSION EXERCISE - MHT CET Corner
15 Videos
- STATIONARY WAVES BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - STATIONARY WAVES EXERCISE - MHT CET Corner
28 Videos
- WAVE MOTIONBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - WAVE MOTIONEXERCISE - MHT CET CORNER
23 Videos
Similar Questions
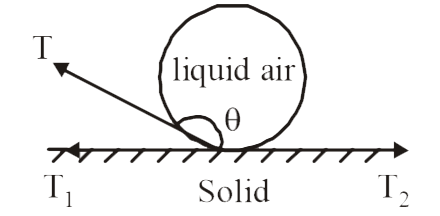
Let T1 be surface tension between solid and air, T2 be the surface tension between solid and liquid and T be the surface tension between liquid and air. Then in equilibrium, for a drop of liquid on a clean glass plate, the correct relation is (θ is angle of contact)
View SolutionThe loss of weight of a solid when immersed in a liquid at 00C is ΔW0. If α and β are the volume coefficients of expansion of the solid and the liquid respectively, then the loss of weight at t∘C is approxumately
View Solution
Knowledge Check
If the surface tension of liquid is T , the work required to increases its surface are by A,is
AA×TBA×2C2A×TDA2×TIf the surface tension of a liquid is T , the gain in surface energy for an increase in liquid surface by A is
AAT−1BATCA2TDA2T−2Internal pressure inside a liquid drop of radius r and surface tension T is
A2Tr−P0B4Tr+P0CP0+2TrDT4r−P0
Where does a solid weigh more: in air or in a liquid?
View SolutionSurface tension of a liquid is independent of the area of surface. Why?
View SolutionCalculate the pressure inside a small air bubble of radus r situated at a depth h below the free surface of liquids of densities ρ1 and ρ2 and surface tennsions T1 and T2. The thickness of the first and second liquids are h1 and h2 respectively. Take atmosphere pressure =P0.

View SolutionIf T is the surface tension of a liquid, the energy needed to break a liquid drop of radius R into 64 drops is
View SolutionIf T is the surface tension of a liquid, the energy needed to break a liquid drop of radius R into 64 drops is :-
View Solution
