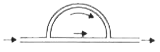
Sound waves are passing through two routes-one in straight path and the other along a semicircular path of radius r and are again combined into one pipe and superposed as shown in the figure. If the velocity of sound waves in the pipe is v, then frequencies of resultant waves of maximum amplitude will be multiples integral of

$\frac{v}{r (π - 2)}$

$\frac{v}{r (v - 1)}$

$\frac{2 v}{r (π - 1)}$

$\frac{v}{r (π + 1)}$

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

Sound waves are passing through two routes- one in straight path and the other along a semicircular path of radius r and are again combined into one pipe and superposed as shown in the figure. If the velocity of sound waves in the pipe is y, then frequencies of resultant waves of maximum amplitude will be integral multiples of

A $\frac{v}{r (π - 2)}$
B $\frac{v}{r (π - 1)}$
C $\frac{2 v}{r (π - 1)}$
D $\frac{v}{r (π + 1)}$
When two sound waves with a phase difference of $π / 2$ , and each having amplitude A and frequency $ω$ , are superimposed on each other, then the maximum amplitude and frequency of resultant wave is
A $\frac{A}{\sqrt{2}} : \frac{ω}{2}$
B $\frac{A}{\sqrt{2}} : ω$
C $\sqrt{2} A : \frac{ω}{2}$
D $\sqrt{2} A : ω$
A sound wave travelling in a medium is represented as shown in the figure.

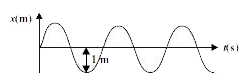
If vibrating source of sound makes 360 oscillations in 2 minutes, then the amplitude, wavelength and frequency of the sound wave are respectively (Take velocity of sound as ${342 m s}^{- 1}$ )
A1 m, 114 m and 3 Hz
B2 m, 3 m and 14 Hz
C1 m, 5 m and 20 Hz
D1 m, 100 m and 10 Hz