The electric field at the centre of a square having equal charge q at each of the coner (side of square a )
8kqa2
2kqa2
zero
4kq(a/√2)2
The correct Answer is:C
To find the electric field at the center of a square with equal charges q at each corner, we can follow these steps:
Step 1: Understand the Configuration
We have a square with side length a and charges q placed at each of the four corners. The center of the square is equidistant from all four charges.
Hint: Visualize the square and label the corners with the charges.
Step 2: Calculate the Distance from the Center to a Corner
The distance R from the center of the square to any corner can be calculated using the Pythagorean theorem. Since the center divides the square into two equal halves, we have:
R=a√2
Hint: Remember that the diagonal of the square can be used to find this distance.
Step 3: Determine the Electric Field Due to One Charge
The electric field E due to a single charge q at a distance R is given by Coulomb's law:
E=k⋅qR2
where k is Coulomb's constant.
Hint: Make sure to substitute R from Step 2 into this formula.
Step 4: Analyze the Direction of the Electric Fields
Each charge produces an electric field pointing away from the charge (if q is positive) or towards it (if q is negative). The electric fields due to opposite charges will have components that cancel each other out.
Hint: Draw vectors for the electric fields from each charge to visualize their directions.
Step 5: Calculate the Net Electric Field
Since the electric fields from opposite corners cancel each other out, we can conclude that the net electric field at the center of the square is zero. Specifically:
- The electric fields due to charges at opposite corners will have equal magnitudes but opposite directions, leading to cancellation.
Hint: Consider symmetry; the configuration is symmetric, which simplifies the analysis.
Conclusion
Thus, the electric field at the center of the square is:
Enet=0
Final Answer
The electric field at the center of the square is zero.
---
We have a square with side length a and charges q placed at each of the four corners. The center of the square is equidistant from all four charges.
The distance R from the center of the square to any corner can be calculated using the Pythagorean theorem. Since the center divides the square into two equal halves, we have:
R=a√2
The electric field E due to a single charge q at a distance R is given by Coulomb's law:
E=k⋅qR2
where k is Coulomb's constant.
Each charge produces an electric field pointing away from the charge (if q is positive) or towards it (if q is negative). The electric fields due to opposite charges will have components that cancel each other out.
Since the electric fields from opposite corners cancel each other out, we can conclude that the net electric field at the center of the square is zero. Specifically:
- The electric fields due to charges at opposite corners will have equal magnitudes but opposite directions, leading to cancellation.
Thus, the electric field at the center of the square is:
Enet=0
The electric field at the center of the square is zero.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELECTROSTATICSEXERCISE - MHT CET Corner
29 Videos
- ELECTROSTATICSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE EXERCISE (Exercise 1 (TOPICAL PROBLEMS))
87 Videos
- ELECTRONS AND PROTONSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELECTRONS AND PROTONSEXERCISE - MHT CET CORNER
19 Videos
- FORCEBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - FORCEEXERCISE - Exercise 2 (Miscellaneous Problems)
19 Videos
Similar Questions
Four identical charges, Q each, are fixed at the vertices of a square. A free charge q is placed at the centre of the square. Investigate the nature of equilibrium of charge q if it is to be displaced slightly along any of the two diagonals of the square.
View SolutionFind the magnetic field at the centre P of square of side a shown in
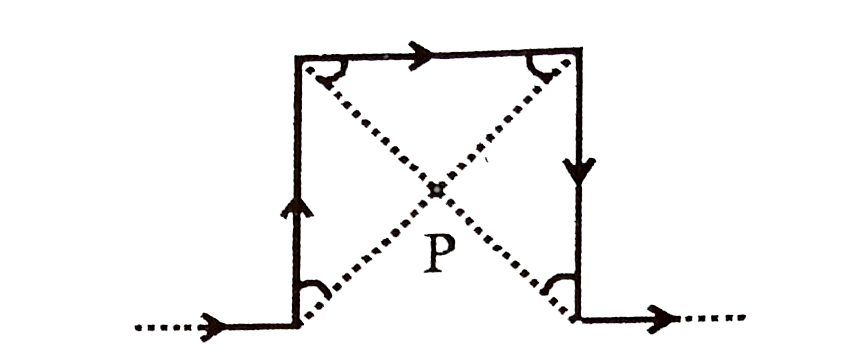 .
.
View Solution
Knowledge Check
The magnetic field at the centre of square of side a is
 A√2μ0πaB√2μ0I3πaC23μ0IaDzero
A√2μ0πaB√2μ0I3πaC23μ0IaDzeroThe magnetic field at the centre of a square coil having side 21 and number of turns n, due to a current I is
A√2μ0nlB√2μ0nl/(πl)C√2μ0nl/lD√2μ0ml/(2l)The magnetic field at the centre of a square coil, having side 21 and number of turns n, due to a current I is
A√2μ0nlB√2μ0nl,l(πl)C√2μ0nllD√2μ0nll(2l)
Eight identical point charges of q coulomb each are placed at the corners of a cube side 0.1m. Calculate electric field at the centre of the cube. Calculate the field at the center when one of the corner charges is removed.
View SolutionA system consists of charges +q and +q at the opposite corners of a square of sides 2a and −q and −q at the other two corners . Calculate the potential and field at a distance r from the centre of the square along a line parallel to the two sides of the square . Assume a <<r .
View SolutionThree charges ,each of +4μC ,are placed at the corners A,B,C of a square ABCD of side 1m.The electric field at the centre O of a square ABCD of side 1m.The electric field at the centre O of the square is
View SolutionFour identical charges i.e. q is placed at the corners of a square of side a. The charge Q that must be placed at the centre of the square such that the whole system of charges in equilibrium is
View SolutionA charge Q is placed at the centre of a square If electric field intensity due to the charge at the corners of the square is E1 and the intensity at the mid point of the sidde of square is E2 then the ratio of E1E2 will be
View Solution
